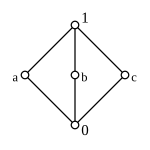
Complement (association theory)
Complementary elements
In a restricted lattice (mathematics) an element is called a complement of if
- and
applies.
A restricted lattice in which every element has (at least) one complement is called a complementary lattice .
In general there can be several complementary elements for one element. If the complement of is unambiguous, different terms are used: it is common for subsets , for applications in logic , for switching algebras .
It applies
- .
In a distributive bounded lattice, each element can have at most one complement.
If a complement has, then also has a complement, namely
- .
A distributive complementary lattice is called a Boolean lattice or Boolean algebra .
Relative complements
If there are elements of a lattice, then the set is called the interval determined by a and b .
The definition is identical to that of a closed interval on ordered sets and the same notation is used.
Are , then the relative complement of relative , if
- and applies.
Here, too, it applies that there can be several elements that are too complementary and that uniqueness follows from the distributive law.
A lattice is called relatively complementary if there is a relative complement for every element in every interval.
A relatively complementary association is a complementary association if and only if it is restricted. Conversely, a complementary association need not be relatively complementary. However, a modular complementary lattice is relatively complementary.
Relative complements can be used to characterize distributive associations. A lattice is distributive if and only if every element has at most one relative complement in every interval.
Pseudo complements
Are two members of a federation, then called a greatest element for which applies a relative Pseudokomplement of respect .
A relative Pseudokomplement of respect is Pseudokomplement of .
A lattice in which there is a pseudo-complement for each element is called a pseudo-complementary lattice.
The designation for pseudo complements is not uniform.
properties
If (relative) pseudo complements exist, then they are uniquely determined.
In a distributive association forms an ideal. Hence the existence of pseudo complements in finite distributive lattices is assured. The distributivity is essential: it is not pseudocomplementary.
For pseudo complements does not have to apply, even if the lattice is distributive. But it always is
- and
One of De Morgan's laws applies to pseudo complements :
For the dual form only applies:
A distributive relatively complementary lattice is called Heyting's algebra .
Orthocomplements
In a lattice, a function is called orthogonalization if it meets the following conditions:
- and
- ,
The lattice (with this illustration) is called the orthocomplementary lattice . is called the orthocomplement of (to this orthogonalization).
If there is a distributive complementary lattice , then the complement of is also its only possible orthocomplement. In general, however, one can also have several different orthogonalizations in a distributive lattice.
Examples of orthocomplements
- If a Euclidean vector space and a sub-vector space , then the vectors which are to be orthogonal form a vector space . and are orthocomplements in the (modular) lattice of the subspaces of .
- The example of the Euclidean vector spaces can be generalized to any vector spaces with an inner product . Various internal products deliver i. A. Various orthocomplements in the union of the subspaces of .
These are typical examples that also led to the naming.
literature
- Gericke Helmuth: Theory of associations . 2nd Edition. BI, Mannheim 1967.
- Grätzer George: Lattice Theory. First concepts and distributive lattices . WHFreeman and Company, 1971, ISBN 978-0-486-47173-0 .
Individual evidence
- ↑ This follows from the reduction rule
- ↑ G. Grätzer, Lattice theory, p. 20. In H. Gericke, Theory of Associations, p. 72 the designation is introduced differently .
- ↑ G. Grätzer, Lattice theory, p. 96.
- ↑ The idea of proof is that in and in each case the reduction rule does not apply, cf. H. Gericke, Theory of Associations, p. 113f
- ↑ G. Grätzer uses a * for the pseudo complement and a * b for the relative pseudo complement (G. Grätzer, Lattice Theory: Foundation, p 99). Gericke uses a mirrored symbol for the designation. (H. Gericke, Theory of Associations, p. 119) Also or occur.
- ↑ H. Gericke, Theory of Associations, p. 120 f. Because of these properties, pseudo-complements can be used to model intuitionist logic .
- ↑ H. Gericke, Theory of Associations, p. 106; however, a clearer designation is used here for the function












![[0, c]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f04abeab39818aa786f2e5f9cdf163379e60c6)


![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![c, d \ in [a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3242edd84bb073a138a9bbf3f4fcf83b3b5d57a5)