Association (mathematics)
An association is in mathematics a structure that both a fine structure as well as algebraic structure can be fully described. As fine structure, a dressing is characterized in that it two elements , a supremum are, d. H. a clearly defined smallest element that is greater than or equal to and , and vice versa an infimum , a largest element that is less than or equal to and . As an algebraic structure, a lattice is characterized by the fact that there are two associative and commutative operations for which the laws of absorption are characteristic: The following applies to any elements
- and .
For every algebraic statement occurring in lattice theory, there is a direct translation into an order statement and vice versa. In most cases, this translation can also be clearly understood. The possibility of interpreting results twice and thus understanding them better makes the investigation and use of statements from association theory so interesting. The term association was coined by Fritz Klein-Barmen in the sense described here.
Although this double characterization looks very special at first glance, associations often occur:
- the z. B. in set theory, logic and Boolean algebras appearing as switching algebras are associations.
- total orders that z. B. in the different number ranges such as ( natural numbers ), ( whole numbers ), ( rational numbers ) or ( real numbers ) are associations.
- for any natural number the set of divisors (ordered by divisibility ) is a lattice.
- the substructures of any algebraic or other structure form a lattice with the subset relation as the order.
In the literature, the symbols and are used instead of and . However, this notation is not used here due to technical restrictions.
In an earlier common terminology , an association (after Richard Dedekind ) was also referred to as a dual group .
Clarification
Associations as algebraic structures
A federation is a set with two internal binary operations (union, engl. Join and) (average, engl. Meet ), the following conditions for all , , from suffice:
- ,
- .
- ,
- .
Absorption laws:
- ,
- .
The idempotency of both connections follows from these conditions :
- ,
- .
is therefore a semi-lattice with respect to each individual connection , i.e. H. a commutative semigroup in which every element is idempotent. The links interact with the laws of absorption.
Associations as organizational structures
According to an idea by Leibniz , one can define a partial order by:
The law of absorption shows the validity of the equivalences
With regard to this partial order, every two-element subset has a supremum (upper limit) and an infimum (lower limit) . An element is a supremum of if:
- and (i.e. is upper bound).
- From and follows (i.e. is the smallest upper bound).
The same applies to the infimum . One can show by induction that every non-empty finite subset has a supremum and an infimum. One generally writes the supremum of a set as , and the infimum of as , if they exist.
Conversely, for a semi-ordered set in which every two-element subset has an infimum and a supremum, one can define:
- and .
The two connections then fulfill the association axioms, as is easy to calculate.
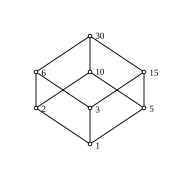
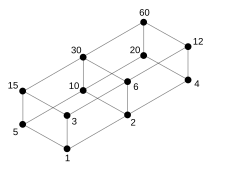
Hasse diagrams for some examples
A finite semi-ordered set can be represented by a directed graph called a Hasse diagram .
If you arrange the graph in such a way that all edges are directed from bottom to top, then you can easily see the order:
- is then equivalent to: is connected to by an edge (leading upwards) .
Special elements in associations
Neutral elements
If the link has a neutral element ,
then it is clearly defined and it is called the zero element of the association. Concerning. is absorbent and the smallest element in terms of order:
- and
The association is then called downwardly restricted .
If the link has a neutral element ,
then it is clearly defined and it is called the element of the association. Concerning. is absorbent and the largest element in terms of order:
- and
The association is then called limited upwards .
A lattice is called restricted if it is restricted below and above, i.e. it has a neutral element for both links.
Complementary elements
For a given element of a restricted lattice, one calls an element with the property
- and
a complement of .
A restricted lattice in which every element has (at least) one complement is called a complementary lattice .
In general, there can be several complementary elements for an element.
However, the following applies: In a distributive restricted lattice, the complement of an element is uniquely determined if it exists . It is often written as (especially with subsets), (especially with applications in logic) or .
In any restricted association applies
- .
In a distributive bounded lattice: If a complement has, then a complement also has, namely:
- .
Special associations
Modular associations
An association is called modular if:
- for everyone .
For an association are in turn equivalent in each case:
- is modular.
- for everyone .
- for everyone .
- for everyone .
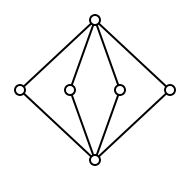
A non-modular association always contains the association as a sub-association.
Distributive Associations
In the following we always mean the association by the association .
A lattice is called distributive if the links are distributive in two respects :
- for everyone and
- for everyone .
Since these two statements are equivalent to each other, it is sufficient to require the validity of one of these two distributive laws.
Every distributive association is modular, but not the other way around. A modular lattice that is not distributive always contains the lattice , the lattice of the subgroups of the Klein group of four as a sublattice.
This gives the test: if a lattice has neither a sublattice of form nor one of form , then it is distributive.
Distributive associations can also be characterized differently, because Birkhoff (1933) and Stone (1936) have shown:
- A lattice is distributive if and only if it is isomorphic to a set .
Boolean algebras
A distributive complementary lattice is called a Boolean algebra or Boolean lattice ;
Another generalization, in which only relative pseudo complements are required instead of complements , is called Heyting algebra .
Complete associations
A lattice is called complete if each (also the empty as well as possibly infinite ) subset has a supremum and an infimum.
It is enough to require the existence of the supremum for each subset , for it is
Each full association is restricted with
- and
Every finite, non-empty lattice is complete and therefore also bounded.
Longitudinal associations
If every subset (chain) that is totally ordered with respect to the order is finite, the lattice is called finite . For many proofs within the lattice theory, a lattice does not have to be finite; it suffices if it is finite.
Compact elements and algebraic associations
An element of a complete lattice is called compact (after the related property of compact spaces in topology ) if every subset of with
contains a finite subset for which the following applies:
A lattice is called algebraic if it is complete and if every element of is the supremum of compact elements.
Duality in associations
If you swap the two links and in an association , you get a new structure . It is called the dual structure.
If one replaces in any formula of the language of lattice theory and uses the two signs and alternately for one another and also replaces 0 by 1 and vice versa, then the resulting formula is called the dual formula of .
Obviously, in the association to be dual, the dual to the formulas in valid apply . Since the dual formula occurs in the definition of an association for every formula, it follows that there is also an association which is referred to as the association that is too dual .
From this observation it follows:
- If one formula applies in all associations, then its dual formula also applies in all associations.
The modularity law is self-dual and the two distributive laws are dual to each other and the two complementary laws are dual to each other. Therefore the following applies accordingly:
- If a formula applies in all modular or in all distributive lattices or in all Boolean algebras, then the dual formula also applies in the corresponding lattices.
Substructures
Sub-associations
A sub-lattice of is a subset that is with the restricted links of a lattice; H. There are
- and in all of
Sub-associations
A sublattice of a subset , which is an association d. H. is a semi-ordered set with supremum and infimum for finite subsets.
Of course, every sub-association is a sub-association, but not the other way around.
Here is one of the few places where you notice the difference in the approach: For associations as organizational structures , all sub-associations are substructures, for associations as algebraic structures , only the sub-associations are substructures.
Neither in the case of sub-associations nor sub-associations is it assumed that the neutral elements will be retained in the substructure. Otherwise you have explicitly by an association with and talk to.
Ideals and filters
An ideal is a sub-association of an association that also fulfills the following condition: are and , then is . (The definition therefore corresponds formally to the definition that one expects in a ring).
Regarding the partial order , however, applies . Therefore the definition can also be interpreted as follows:
- An ideal is a sub-lattice that, together with an element, also contains all elements of that are smaller than .
Filters are defined dual to ideals:
- A filter is a sub-lattice that, together with an element, also contains all elements of that are greater than .
Homomorphisms
Are and two associations and a function such that for all of true
then is called association homomorphism . Is also bijective , then is called association isomorphism and the associations and are isomorphic .
If and are complete and even
fulfilled for all is called a complete association homomorphism. Any complete lattice homomorphism is obviously also a lattice homomorphism.
The class of all associations forms a category with these homomorphisms .
An association homomorphism is at the same time an order homomorphism, i. H. an isotonic figure :
- from follows
However, not every isotonic mapping between lattices is a lattice homomorphism.
The following applies in restricted lattices: The set of elements of which are mapped onto the zero element of the image by means of a lattice homomorphism form an ideal of and dual, the set of elements which are mapped to the single element form a filter.
More examples of associations
Totally ordered sets
Every totally ordered set is a distributive lattice with the links maximum and minimum . In particular, for all , , from :
- ,
- .
The association is complementary only in the case of a one- or two-element set .
Examples of the other properties:
- The closed real interval and the extended real line ( with and ) are each complete distributive lattices (and thus bounded).
- The open real interval , the sets , and are each incomplete unbounded distributive lattices.
- The rational interval is an incomplete bounded distributive lattice.
- The set is an incomplete distributive lattice with a zero element .
Divider associations
If one considers the set of all divisors of for a natural number , then is a complete distributive lattice with one element (neutral element for GCD ) and zero element (neutral element for LCM ). It is called the divider lattice of . The absorption laws and distributive laws for gcd and lcm follow z. B. with the prime factorization from the properties of max and min, but it can also be derived from considerations of divisibility. The lattice is complementary (and therefore Boolean ) if and only if is square-free, i.e. H. if has no square number as a divisor. The partial order on is the divisor relation:
- exactly if (exactly if ).
Subsets
For a set , the power set with the links union and average forms an algebraic Boolean lattice with zero element (neutral element with regard to ) and one element (neutral element with regard to ) as well as complement for all . It is called a power set or subset of . The partial order on is the quantity inclusion:
- if (or equivalent to )
(Carrier quantities of) sub- grouping (s) of hot group groups (there is often no distinction between the groups and their carrier groups). These associations are always distributive, but do not have to be complete or have neutral elements or complements. (An example of this is the association of the right-infinite real intervals with from , which is isomorphic to the association of the real numbers.)
Sub-structural associations of algebraic structures, sub-group associations
For one group the amount is all subgroups of an algebraic (generally not modular and therefore not distributive) association with the links product of the union and average. It is called subgroup association of .
For example, the subgroup lattice of the small group of four , which just corresponds to the lattice, is non-distributive but modular.
Likewise educate
- the normal subgroups of a group,
- the subgroups of an Abelian group,
- the sub-rings of a ring ,
- the lower body of a body ,
- the sub-modules of a module ,
- the ideals of a ring
a modular algebraic lattice with analog connections. The subgroups of any group and the sublattices of any lattice always result in an algebraic lattice, but this does not have to be modular.
In general, the substructures of an algebraic structure always form an algebraic lattice (whereby the empty set is also regarded as a substructure if the set-theoretical average - i.e. the infimum with respect to the set inclusion - of the set of all substructures is empty).
In particular, a lattice is algebraic if and only if it is isomorphic to the lattice of the substructures of an algebraic structure (hence the name algebraic lattice).
If the number of subgroups is restricted to main groups of a fixed subgroup , then all of these intermediate groups also form a restricted association. Analogous to this, there are associations of intermediate rings, intermediate bodies, intermediate modules, intermediate ideals.
One is particularly interested in the subgroup association of the Galois group of a Galois body extension , because it is isomorphic to the dual interbody association of .
literature
- Rudolf Berghammer: Orders, associations and relations with applications . 2nd Edition. Springer + Vieweg, Wiesbaden 2012, ISBN 978-3-658-00618-1 .
- Garrett Birkhoff : Lattice Theory . 3. Edition. AMS, Providence RI 1973, ISBN 0-8218-1025-1 .
- Hilda Draškovičová: Ordered Sets and Lattices . AMS, 1992, ISBN 0-8218-3121-6 .
- Hans Hermes : Introduction to Association Theory . 2nd Edition. Springer-Verlag, Berlin / Heidelberg 1967.
- Heinz Liermann: Association structures in mathematics lessons . Diesterweg Salle, Frankfurt a. M. 1971, ISBN 3-425-05317-5 .
- Gábor Szász: Introduction to Association Theory . Akademiai Kiado, Budapest 1962.
Web links
References and comments
- ^ Leo Corry: Modern Algebra and the Rise of Mathematical Structures , Springer, 2004, ISBN 3-7643-7002-5 , p. 267
- ↑ H. Gericke, Theory of Associations . 2nd Edition. Mannheim 1967, p. 76 (figure on p. 70)
- ↑ H. Gericke, Theory of Associations . 2nd Edition. Mannheim 1967, p. 111
- ↑ G. Grätzer, Lattice Theory , 1971, p. 75
- ↑ Helmuth Gericke: Theory of Associations . Bibliographisches Institut, Mannheim 1963, § 6.2



















































































































![[0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)



![[0,1] \ cap \ mathbb {Q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97119403d3148dbf45f6e697c559c2e44fce8a9)