Modular association

Hate diagram of , the smallest non-modular association. ${\displaystyle N_{5}}$

A modular association in the sense of order theory is an association that fulfills the following self-dual condition (modularity law):

${\displaystyle x\leq b}$ implies ${\displaystyle x\vee (a\wedge b)=(x\vee a)\wedge b.}$

Modular associations occur in algebra and many other areas of mathematics. For example, the sub-vector spaces of a vector space (and more generally the sub-modules of a module over a ring ) form a modular lattice.

Each distributive association is modular.

In a non-modular association, there can still be elements that meet the modularity law together with any elements and (under the condition ). Such an element is called a modular element . Pairs of elements that satisfy the modularity law for all elements can be considered even more generally . Such a pair is called a modular pair , and there are several semimodularity- related generalizations of modularity that build on this term. ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle x\leq b}$ ${\displaystyle b}$ ${\displaystyle (a,b)}$ ${\displaystyle x}$

introduction

The modularity law can be understood as a restricted associative law, which links the two lattice operations in a similar way as the associative law for vector spaces combines the field multiplication with the scalar multiplication. The restriction is necessary because it follows from . ${\displaystyle \lambda (\mu x)=(\lambda \mu )x}$ ${\displaystyle x\leq b}$ ${\displaystyle x\vee (a\wedge b)=(x\vee a)\wedge b}$

Non-modularity of . ${\displaystyle N_{5}}$

One can easily check that it follows from in each association . Therefore, the modularity law can also be formulated as follows: ${\displaystyle x\leq b}$ ${\displaystyle x\vee (a\wedge b)\leq (x\vee a)\wedge b}$

Modularity law (variant)

${\displaystyle x\leq b}$implies . ${\displaystyle x\vee (a\wedge b)\geq (x\vee a)\wedge b}$

By substituting for the term , the modularity law can be expressed as follows by an equation that must be fulfilled without preconditions: ${\displaystyle x}$ ${\displaystyle x\wedge b}$

${\displaystyle (x\wedge b)\vee (a\wedge b)=\left[(x\wedge b)\vee a\right]\wedge b}$.

This shows (using terms from universal algebra ) that the modular lattices form a sub-variety of the variety of lattices. Therefore, all homomorphic images, sub-associations and direct products of modular associations are modular again.

The smallest non-modular lattice is the "Pentagon lattice" , which consists of five elements , so that , and is not comparable with or with . For this association applies , in contradiction to the modularity law. Each non-modular association has a copy of as a sub-association. ${\displaystyle N_{5}}$ ${\displaystyle 0,1,x,a,b}$ ${\displaystyle 0<x<b<1,0<a<1}$ ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle b}$ ${\displaystyle x\vee (a\wedge b)=x\vee 0=x<b=1\wedge b=(x\vee a)\wedge b}$ ${\displaystyle N_{5}}$

According to Richard Dedekind , who discovered the modularity law, modular associations are sometimes still referred to as Dedekind associations today .

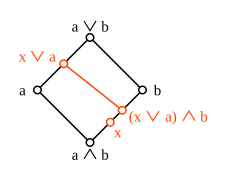
Diamond isomorphism theorem

The intervals and can be considered for every two elements of a modular association . Between them there are the order-maintaining images ${\displaystyle a,b}$ ${\displaystyle \left[a\wedge b,b\right]}$ ${\displaystyle \left[a,a\vee b\right]}$

${\displaystyle \phi \colon \left[a\wedge b,b\right]\to \left[a,a\vee b\right]}$ and

${\displaystyle \psi \colon \left[a,a\vee b\right]\to \left[a\wedge b,b\right]}$,

defined by and . ${\displaystyle \phi (x)=x\vee a}$ ${\displaystyle \psi (x)=x\wedge b}$

• 

  In a modular association, the indicated images and isomorphisms are inverse to one another. ${\displaystyle \phi }$ ${\displaystyle \psi }$

• 

  Counterexample to the diamond isomorphism theorem in a non-modular lattice

The composition is an order-preserving map of the interval in itself, which also satisfies the inequality . The example shows that this inequality i. A. Doesn't have to be an equation. In a modular association, however, the equation always applies. Since the dual association is again modular to a modular association, the identity mapping is also on ; therefore and are isomorphisms between these two intervals. ${\displaystyle \psi \phi }$ ${\displaystyle \left[a\wedge b,b\right]}$ ${\displaystyle \psi (\phi (x))=(x\vee a)\wedge b\geq x}$ ${\displaystyle \phi \psi }$ ${\displaystyle \left[a,a\vee b\right]}$ ${\displaystyle \phi }$ ${\displaystyle \psi }$

This set is known as the isomorphism set for modular lattices, or sometimes the diamond isomorphism set (for modular lattices). A lattice is modular if and only if the diamond isomorphism theorem holds for every pair of elements.

The isomorphism theorem for modular organizations is analogous to third isomorphism theorem in algebra, and he is a generalization of the association set .

Modular pairs

The centered hexagon lattice , also known as , is M-symmetric but not modular. ${\displaystyle S_{7}}$ ${\displaystyle D_{2}}$

In every association, a modular pair is understood to be a pair of elements, so that the equation applies to all elements that satisfy . In other words, the modular pairs are the pairs to which one half of the diamond isomorphism theorem applies. The French term for "modular couple" is couple modulaire . A pair is called paire modulaire in French , if both and are modular pairs. A bond element is called a modular element (right) if the pair is modular for all elements . ${\displaystyle (a,b)}$ ${\displaystyle x}$ ${\displaystyle a\wedge b\leq x\leq b}$ ${\displaystyle (x\vee a)\wedge b=x}$ ${\displaystyle (a,b)}$ ${\displaystyle (a,b)}$ ${\displaystyle (b,a)}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle (a,b)}$

Some associations have the property that for every modular pair the pair is also modular. Such a bandage is called an M-symmetrical bandage . Some authors, for example Fofanova, refer to such associations as semi-modular associations . Since every M-symmetric lattice is semimodular and the converse also applies to lattices of finite length, this can only lead to confusion for certain infinite lattices . Since a lattice is modular if and only if every pair of elements is modular, every modular lattice is M-symmetric. In the association described above, the pair is modular, but not the pair . Hence it is not M-symmetric. The centered hexagon lattice is M-symmetrical, but not modular. Since is a sublattice of , the M-symmetric lattices do not form a sub-variety of the variety of lattices. ${\displaystyle (a,b)}$ ${\displaystyle (b,a)}$ ${\displaystyle N_{5}}$ ${\displaystyle (b,a)}$ ${\displaystyle (a,b)}$ ${\displaystyle N_{5}}$ ${\displaystyle S_{7}}$ ${\displaystyle N_{5}}$ ${\displaystyle S_{7}}$

M-symmetry is not a self-dual term. A dual-modular pair is a pair that is modular in the dual lattice , and a lattice is called dual M-symmetric or M ^* -symmetric if the dual lattice is M-symmetric. One can show that a finite lattice is modular if and only if it is M-symmetric and M ^* -symmetric. The same equivalence holds for infinite lattices that satisfy the ascending chain condition (or the descending chain condition).

Some less important terms are closely related to this. A lattice is called cross-symmetric if the pair is dual modular for every modular pair . Cross symmetry implies M symmetry, but not M ^* symmetry. Hence, cross symmetry is not equivalent to dual cross symmetry. A lattice with a smallest element 0 is called ⊥-symmetric if for every modular pair that satisfies the pair is also modular. ${\displaystyle (a,b)}$ ${\displaystyle (b,a)}$ ${\displaystyle (a,b)}$ ${\displaystyle a\wedge b=0}$ ${\displaystyle (b,a)}$

See also

• Dedekind's modular law
• Modular group (M group)

literature

• Garrett Birkhoff : Lattice Theory . 3. Edition. AMS, Providence, RI 1973, ISBN 0-8218-1025-1 .
• Richard Dedekind : About the dual group created by three modules . In: Mathematical Annals . tape 53 , no. 3 , September 1, 1900, ISSN  0025-5831 , p. 371-403 , doi : 10.1007 / BF01448979 .
• George Grätzer: General Lattice Theory . 2nd Edition. Birkhäuser, Basel / Boston 1998, ISBN 3-7643-5239-6 .
• Hans Hermes : Introduction to Association Theory (= B. Eckmann, BL van der Waerden [Hrsg.]: Basic teachings of the mathematical sciences in individual presentations with special consideration of the areas of application . Volume 73 , no. 7 ). 2nd Edition. Springer, Berlin / Heidelberg 1967, doi : 10.1007 / 978-3-642-86524-4 .
• LA Skornyakov: Modular lattice . In: Encyclopaedia of mathematics . Springer, Berlin / Heidelberg 2001, ISBN 1-4020-0609-8 ( eom.springer.de ).
• Gábor Szász: Introduction to Association Theory . Akademiai Kiado, Budapest 1962, OCLC 13475544 .

Web links

• Modular lattice at Planet Math