Associative law

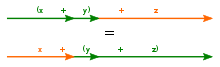
With associative links, the end result is the same even if the operations are performed in a different order.

The associative law ( Latin associare "unite, connect, link, network"), in German linkage law or connection law , is a rule from mathematics . A ( two-digit ) link is associative if the order of execution is not important. In other words: The bracketing of several associative links is arbitrary. That is why it can be clearly called the “law of brackets”.

In addition to the associative law, the commutative law and the distributive law are of elementary importance in algebra .

definition

A binary connection on a set is called associative if the associative law applies to all ${\displaystyle {\star }\colon A\times A\to A}$ ${\displaystyle A}$ ${\displaystyle a,b,c\in A}$

${\displaystyle a\star \left(b\star c\right)=\left(a\star b\right)\star c}$

applies. The brackets can then be omitted. This also applies to more than three operands .

Examples and counterexamples

The associativity of adding real numbers

As links on the real numbers , addition and multiplication are associative. For example

${\displaystyle (2+3)+7=5+7=12\quad =}$

${\displaystyle 2+(3+7)=2+10=12}$

and

${\displaystyle (2\cdot 3)\cdot 7=6\cdot 7=42\quad =}$

${\displaystyle 2\cdot (3\cdot 7)=2\cdot 21=42}$ .

Real subtraction and division , however, are not associative because it is

${\displaystyle 2-(3-1)=0\quad \neq }$

${\displaystyle (2-3)-1=-2}$

and

${\displaystyle (4:2):2=1\quad \neq }$

${\displaystyle 4:(2:2)=4}$ .

The potency is not associative either

${\displaystyle 2^{(2^{3})}=2^{8}=256\quad \neq }$

${\displaystyle (2^{2})^{3}=4^{3}=64}$

applies. In the case of (divergent) infinite sums , the brackets may be important. Addition loses associativity for:

${\displaystyle (1+(-1))+(1+(-1))+(1+(-1))+(1+(-1))+\ldots =0+0+\ldots \to 0}$

but

${\displaystyle 1+((-1)+1)+((-1)+1)+((-1)+1)+\ldots =1+0+0+\ldots \to 1}$

classification

The associative law belongs to the group axioms , but is already required for the weaker structure of a semigroup .

Laterality

→ Main article : Operator associativity

In the case of non-associative links in particular, there are conventions of side associativity.

A binary link is considered to be left-associative if ${\displaystyle *}$

${\displaystyle {\begin{array}{ll}a*b*c&:=(a*b)*c\qquad \qquad \quad \,\\a*b*c*d&:=((a*b)*c)*d\quad \\{\mbox{etc.}}\end{array}}}$

is to be understood.

• The non-associative operations subtraction and division are commonly understood to be left-associative:

	${\displaystyle a-b-c}$	${\displaystyle =(a-b)-c}$	( Subtraction )
	${\displaystyle a:b:c}$	${\displaystyle =(a:b):c}$	( Division )

• Application of functions in the process of currying .
  ${\displaystyle (f\,x\,y)=((f\,x)\,y)}$
  

A binary connection is called right-associative if the following applies: ${\displaystyle *}$

${\displaystyle {\begin{array}{rr}x*y*z:=&x*(y*z)\\w*x*y*z:=&w*(x*(y*z))\\&{\mbox{etc.}}\end{array}}}$

Example of a right-associative operation:

• Exponentiation of real numbers in exponent notation:

${\displaystyle x^{y^{z}}=x^{(y^{z})}}$

But associative operations can also have sidedness if they can be iterated to infinity.

• The decimal notation right of the decimal is a left-associative linking of the decimal number, because the evaluation (sschleife) is not right with the ellipsis can begin, but must start on the left.
  ${\displaystyle 0{,}999\ldots =0{,}9999\ldots =0{,}99999\ldots \to 1}$
  ${\displaystyle \ldots }$
• The -adic notation contains a right-associative chaining operation with the juxtaposition , because the evaluation must begin on the right. ${\displaystyle p}$
  ${\displaystyle \ldots 444_{5}=\ldots 4444_{5}=\ldots 44444_{5}\to -1}$
  

Weaker forms of associativity

The following weakening of the associative law is mentioned / defined elsewhere:

• Potency Associativity :
  ${\displaystyle a^{r+s}=(a^{r})\circ (a^{s})}$
  • i-power associativity :
    ${\displaystyle a^{i}\circ a=a\circ a^{i}}$
  • Idem associativity :
    ${\displaystyle a\circ (a\circ a)=(a\circ a)\circ a}$
• Alternative :
  • Left alternative :
    ${\displaystyle a\circ (a\circ b)=(a\circ a)\circ b}$
  • Legal alternativity :
    ${\displaystyle a\circ (b\circ b)=(a\circ b)\circ b}$
• Flexibility law :
  ${\displaystyle a\circ \left(b\circ a\right)=\left(a\circ b\right)\circ a}$
• Moufang identities :
  ${\displaystyle {\Big (}a\circ (b\circ a){\Big )}\circ c=a\circ {\Big (}b\circ (a\circ c){\Big )}}$
  ${\displaystyle (a\circ b)\circ (c\circ a)=a\circ {\Big (}(b\circ c)\circ a{\Big )}}$
• Bol identities:
  • left Bol identity:
    ${\displaystyle {\Big (}b\circ (c\circ b){\Big )}\circ a=b\circ {\Big (}c\circ (b\circ a){\Big )}}$
  • right Bol identity:
    ${\displaystyle {\Big (}(a\circ b)\circ c{\Big )}\circ b=a\circ {\Big (}(b\circ c)\circ b{\Big )}}$
• Jordan Identity :
  ${\displaystyle a\circ {\Big (}\left(a\circ a\right)\circ b{\Big )}=\left(a\circ a\right)\circ \left(a\circ b\right)}$

See also

• algebra
• Operator associativity

literature

• Otto Forster: Analysis 1: differential and integral calculus of a variable . Vieweg-Verlag, Munich 2008, ISBN 978-3-8348-0395-5 .

Individual evidence

1. ^ Bronstein: Pocket book of mathematics . Chapter: 2.4.1.1, ISBN 978-3-8085-5673-3 , pp. 115-120
2. ^ George Mark Bergman: Order of arithmetic operations
3. ^ The Order of Operations. Education Place
4. ↑ Gerrit Bol: Web and Groups In: Mathematische Annalen , 114 (1), 1937, pp. 414-431.