Currying

Currying (especially in linguistics, also Schönfinkeln ) is the conversion of a function with several arguments into a sequence of functions with one argument each. Although the process was invented by Moses Schönfinkel in 1928 and thought ahead by Gottlob Frege around 1900, it is often named after Haskell Brooks Curry , who developed the process extensively in theory in 1958.

Procedure

Given a function that takes n  arguments. If this is applied to an  argument, it only consumes this and delivers another function as a function value that still requires arguments. The returned function is then applied to all further arguments. ${\displaystyle n-1}$

Expressed in types, it is a matter of converting a function to a modified function . ${\displaystyle f\colon A_{1}\times \ldots \times A_{n}\to B}$ ${\displaystyle f_{curried}\colon A_{1}\to (A_{2}\to (\ldots (A_{n}\to B)\ldots ))}$

An alternative notation is , which is understood as an operator that modifies -digit mapping (for ) to a single-digit mapping, the image values ​​of which are single-digit mapping, etc., whereby all arguments of the original mapping are run through in sequence; formally: ${\displaystyle \operatorname {curry} (f)=f_{curried}}$ ${\displaystyle \operatorname {curry} }$ ${\displaystyle n}$ ${\displaystyle n>1}$

${\displaystyle \operatorname {curry} \colon (A_{1}\times \ldots \times A_{n}\to B)\,\to \,(A_{1}\to (A_{2}\to (\ldots (A_{n}\to B)\ldots )))}$.

The concept of currying is related, but (for ) different, from that of partial application such as: ${\displaystyle n>2}$

${\displaystyle f(a_{1},a_{2},\ldots a_{n-1},\cdot )\colon A_{n}\to B,a_{n}\mapsto f(a_{1},a_{2},\ldots a_{n})}$,

${\displaystyle f(a_{1},\underbrace {\cdot ,\ldots ,\cdot } _{(n-1){\text{-mal}}}))\colon A_{2}\times \ldots \times A_{n}\to B,(a_{2},\dots ,a_{n})\mapsto f(a_{1},a_{2},\ldots a_{n})}$.

In the single-digit case ( ), currying has no effect: ${\displaystyle n=1}$

${\displaystyle f_{curried}=f}$,

in the two-digit case ( ) there is a connection ${\displaystyle n=2}$

${\displaystyle f_{curried}\colon A_{1}\to (A_{2}\to B),a_{1}\mapsto f(a_{1},\cdot )}$, d. H. for everyone : ${\displaystyle a_{1}\in A_{1}}$

${\displaystyle f_{curried}(a_{1})=f(a_{1},\cdot )}$,

in the three-digit case ( ) applies to : ${\displaystyle n=3}$ ${\displaystyle a_{1}\in A_{1}}$

${\displaystyle f_{curried}(a_{1})\colon A_{2}\to (A_{3}\to B),a_{2}\mapsto f(a_{1},a_{2},\cdot )}$, and additionally : ${\displaystyle a_{2}\in A_{2}}$

${\displaystyle f_{curried}(a_{1})(a_{2})\colon A_{3}\to B,a_{3}\mapsto f(a_{1},a_{2},\cdot )}$, d. H. , ${\displaystyle f_{curried}(a_{1})(a_{2})=f(a_{1},a_{2},\cdot )}$

general:

${\displaystyle f_{curried}(a_{1})(a_{2})\dots (a_{n})=f(a_{1},a_{2},\dots ,a_{n})}$,

${\displaystyle f_{curried}(a_{1})(a_{2})\dots (a_{n-1})=f(a_{1},a_{2},\dots ,a_{n-1},\cdot )}$.

In general, it often happens that a multi-digit mapping is not defined for all value combinations from the carrier sets , i.e. only for a subset of the Cartesian product , i.e. H. on (the graph of) a relation . This situation can be dealt with by either permitting partial mappings in principle and adopting the above definitions formally. If, on the other hand, you stick to the concept of total mappings, the areas of definition of the mappings involved will depend on the choice of parameters that have already been defined, as the example of two-digit maps shows: ${\displaystyle A_{1},\dots ,A_{n}}$ ${\displaystyle R=D_{f}\subseteq A_{1}\times \cdots \times A_{n}}$

${\displaystyle f_{curried}(a_{1})=f(a_{1},\cdot )}$;

the definition range of this figure depends on: ${\displaystyle a_{1}}$

${\displaystyle \{a_{2}\in A_{2}|\exists a_{1}\in A_{1}:(a_{1},a_{2})\in D_{f}\}=R^{\leftarrow }(\{a\})}$,

thus the archetypal fiber of the domain of definition understood as a relation . ${\displaystyle a_{1}}$ ${\displaystyle R=D_{f}}$

As is true for n = 1 , can for be used as for the same symbol . This is called overloading (see also signature (model theory) §Notes ). ${\displaystyle f_{curried}=f}$ ${\displaystyle f_{curried}}$ ${\displaystyle f}$

Examples

Lambda notation

An example in lambda notation is intended to clarify the procedure, whereby the function is specifically defined as follows:

${\displaystyle \lambda x\ y\ z\ .\ x\ y\ z}$

The function therefore requires 3 arguments and returns them. The definition is equivalent to:

${\displaystyle \lambda x.\lambda y.\lambda z\ .\ x\ y\ z}$

When the function is applied to arguments a, b, and c, the following happens:

${\displaystyle \left(\lambda x.\lambda y.\lambda z\ .\ x\ y\ z\right)\ a\ b\ c\ {\mathsf {-\ Die\ Anwendung}}}$

${\displaystyle \left(\lambda y.\lambda z\ .\ a\ y\ z\right)\ b\ c}$

${\displaystyle \left(\lambda z\ .\ a\ b\ z\right)\ c}$

${\displaystyle a\ b\ c\ {\mathsf {-\ Resultat}}}$

After the function has been applied to a , b and  c for the first time , x in the function body is replaced by the first argument  a . The result is a function that still requires the arguments y and z . This is immediately applied to b and  c .

Overload

Suppose we have a two digit multiplication function that multiplies two integers; H. assigns its product to a pair of whole numbers: ${\displaystyle \operatorname {mult} }$

${\displaystyle \operatorname {mult} \colon \,{\begin{cases}\mathbb {N} \times \mathbb {N} \to \mathbb {N} \\(m,n)\mapsto m*n\end{cases}}}$ With ${\displaystyle \operatorname {mult} (m,n)=m*n}$ 

By definition, this function applies to two natural numbers and returns a natural number, for example . ${\displaystyle \operatorname {mult} (2,3)=6}$

If the first argument is now filled (for example with ), the second is left blank, a single-digit ' higher function ' is created, which itself accepts a (further) argument and returns the product with this fixed parameter (the number ): ${\displaystyle 2}$ ${\displaystyle 2}$

${\displaystyle \operatorname {mult} (2,\cdot )\colon \,}$  ${\displaystyle {\begin{cases}\mathbb {N} \to \mathbb {N} \\n\mapsto 2*n\end{cases}}}$

and for any fixed first argument : ${\displaystyle m\in \mathbb {N} }$

${\displaystyle \operatorname {mult} (m,\cdot )\colon \,}$  ${\displaystyle {\begin{cases}\mathbb {N} \to \mathbb {N} \\n\mapsto m*n\end{cases}}\,}$ .

With an n-digit function, currying means carrying out this process until only a single-digit higher function remains. For n = 2 we have:

${\displaystyle \operatorname {mult} _{curried}\colon \,{\begin{cases}\mathbb {N} \to (\mathbb {N} \to \mathbb {N} )\\m\mapsto \operatorname {mult} (m,\cdot )\end{cases}}\,}$ 

Since the designation as a one-digit function is still vacant, it can be overloaded, i. H. digit case, as understood: ${\displaystyle \operatorname {mult} }$ ${\displaystyle \operatorname {mult} }$ ${\displaystyle \operatorname {mult} _{curried}}$

${\displaystyle \operatorname {mult} (m)(n)=\operatorname {mult} _{curried}(m)(n)=\operatorname {mult} (m,n)=m*n}$.

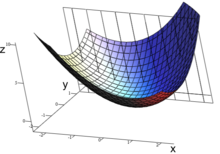
Geometric example

f (x, y) = x ^ 2 + xy + y ^ 2

The situation for a function with two arguments can be imagined as follows: Fixing an argument variable corresponds to a restriction of the two-dimensional definition set to a one-dimensional subset, e.g. B. , the resulting function corresponds to the intersection of the graph of with the plane of all points . All points of the graph can thus also be reached through a two-stage selection: first by defining the cutting plane and then by evaluating the cutting curve at the point . ${\displaystyle z=f(x,y)}$ ${\displaystyle y=1}$ ${\displaystyle f(x,y)}$ ${\displaystyle (x,1,z)}$ ${\displaystyle (x,y,z)}$ ${\displaystyle y=1}$ ${\displaystyle s(x)=f(x,y)|_{y=1}}$ ${\displaystyle x}$

application

Currying is mostly used in programming languages ​​and calculi, in which functions can only receive a single argument. These include, for example, ML , Unlambda and the lambda calculus as well as the Haskell named after Curry . However, many of these languages ​​offer the programmer syntactic possibilities to disguise this. An example of this is the equivalence of the function definition in the example shown above .

JavaScript

The following example shows currying in JavaScript . First, a function is uncurried_adddefined that has the sum of the two arguments as the result. On the other hand, a function is curried_adddefined that returns a function defined as a closure that can be partially applied.

function uncurried_add(x, y) {
    return x + y;
}

function curried_add(x) {
    return function(y) {
        return x + y;
    };
}

console.log(uncurried_add(3, 5)); // 8
console.log(curried_add(3)(5)); // 8

const add_three = curried_add(3);
console.log(add_three(5)); // 8
console.log(add_three(12)); // 15

The function is partially applied by currying, whereby the function arguments are passed one after the other and are temporarily held in a new function that can be used any further.

The functions can also be defined more briefly in JavaScript using the lambda notation:

const uncurried_add = (x, y) => x + y;
const curried_add = x => y => x + y;

Java

import java.util.function.*; 

class Main {
    static IntBinaryOperator uncurried_add = (x, y) -> x + y;
    static IntFunction<IntUnaryOperator> curried_add = x -> y -> x + y;

    public static void main(String[] args) {
        System.out.println(uncurried_add.applyAsInt(3, 5)); // 8
        System.out.println(curried_add.apply(3).applyAsInt(5)); // 8

        var add_three = curried_add.apply(3);
        System.out.println(add_three.applyAsInt(5)); // 8
        System.out.println(add_three.applyAsInt(12)); // 15
    }
}

Kotlin

val uncurried_add = { x: Int, y: Int -> x + y }
val curried_add = { x: Int -> { y: Int -> x + y } }

println(uncurried_add(3, 5)) // 8
println(curried_add(3)(5)) // 8

val add_three = curried_add(3)
println(add_three(5)) // 8
println(add_three(12)) // 15

C ++

C ++ introduced the anonymous function lambda calculus to the language. With the keyword auto, the data type is implicitly derived through type inference , without having to declare the data type explicitly. This results in a shorter notation for the curriculum:

#include <iostream>

using namespace std;

int uncurried_add(int x, int y) {
    return x + y;
}

auto curried_add(int x) {
    return [x](int y) { return x + y; };
}

int main() {
    cout << uncurried_add(3, 5) << endl; // 8
    cout << curried_add(3)(5) << endl; // 8

    auto add_three = curried_add(3);
    cout << add_three(5) << endl; // 8
    cout << add_three(12) << endl; // 15

    return 0;
}

Note that the mention of the type intin the argument of the lambda expression can also be autoreplaced with, which generalizes the implementation. However, the parameters of the named function curried_addcan only be generalized by templates for different data types.

C.

Since there are no anonymous functions in the C programming language , a named function that is returned by is adddefined separately curried_add. The value of xis zstored in the global variable , as the function addcannot access the continuation of the function curried_add.

#include <stdio.h>

int uncurried_add(int x, int y) {
    return x + y;
}

int z;

int add(int y) {
    return y + z;
}

typedef int function(int);

function* curried_add(int x) {
    z = x;
    return add;
}

int main() {
    printf("%d\n", uncurried_add(3, 5)); // 8
    printf("%d\n", curried_add(3)(5)); // 8

    function* add_three = curried_add(3);
    printf("%d\n", add_three(5)); // 8
    printf("%d\n", add_three(12)); // 15

    return 0;
}

C #

using System;

class Program {
    delegate int Method(int x, int y);
    delegate Func<int, int> Curry(int x);

    static Method uncurried_add = (x, y) => x + y;
    static Curry curried_add = x => y => x + y;

    public static void Main() {
        Console.WriteLine(uncurried_add(3, 5)); // 8
        Console.WriteLine(curried_add(3)(5)); // 8

        var add_three = curried_add(3);
        Console.WriteLine(add_three(5)); // 8
        Console.WriteLine(add_three(12)); // 15
    }
}

F #

let uncurried_add (x, y) = x + y
let curried_add x y = x + y

printfn "%i" (uncurried_add (3, 5)) // 8
printfn "%i" ((curried_add 3) 5) // 8
printfn "%i" (curried_add 3 5) // 8

let add_three = curried_add 3
printfn "%i" (add_three 5) // 8
printfn "%i" (add_three 12) // 15

Haskell

In the Haskell programming language , a function can have exactly one parameter or no parameter. If you want to call a function with multiple arguments, the arguments must first be put together in a new object so that the function receives only one argument. The parameters can be listed in round brackets separated by commas to define a tuple .

uncurried_add (x, y) = x + y

An alternative to this is currying. In the explicit notation, one defines a function with only one argument for each value in the tuple. As long as not all arguments have been passed, a function is returned that returns a partial result.

curried_add x = \y -> x + y

Since the notation with several lambda functions can be cumbersome, there is a syntactically sugar-coated notation that is semantically equivalent. If you write the arguments behind one another without round brackets, you automatically get a currified function.

curried_add x y = x + y

The currified function can be used both explicitly and implicitly in part.

main = do
    print (uncurried_add (3, 5)) -- 8
    print ((curried_add 3) 5) -- 8
    print (curried_add 3 5) -- 8

    let add_three = curried_add 3
    print (add_three 5) -- 8
    print (add_three 12) -- 15

In addition, Haskell offers the option of converting a function between a currified and a non-currified definition. The functions curryand uncurryare used for this.

main = do
    let uncurried = uncurry curried_add
    print (uncurried (3, 5)) -- 8
    
    let curried = curry uncurried_add
    print ((curried 3) 5) -- 8
    print (curried 3 5) -- 8

    let add_three = curried 3
    print (add_three 5) -- 8
    print (add_three 12) -- 15

python

def uncurried_add(x, y):
    return x + y

def curried_add(x):
    return lambda y: x + y

print(uncurried_add(3, 5)) # 8
print(curried_add(3)(5)) # 8

add_three = curried_add(3)
print(add_three(5)) # 8
print(add_three(12)) # 15

Ruby

def uncurried_add(x, y)
    return x + y
end

def curried_add(x)
    return lambda { |y| x + y }
end

puts uncurried_add(3, 5) # 8
puts curried_add(3).call(5) # 8

add_three = curried_add(3)
puts add_three.call(5) # 8
puts add_three.call(12) # 15

In the Ruby programming language there is also the option of currifying a function object only when the function is called.

uncurried_add = lambda { |x, y| x + y }
puts uncurried_add.call(3, 5) # 8
puts uncurried_add.curry[3][5] # 8

add_three = uncurried_add.curry[3]
puts add_three.call(5) # 8
puts add_three.call(12) # 15

Scheme

(define uncurried-add (lambda (x y)
    (+ x y)))

(define curried-add (lambda (x)
    (lambda (y)
        (+ x y))))

(display (uncurried-add 3 5)) (newline) ; 8
(display ((curried-add 3) 5)) (newline) ; 8

(define add-three (curried-add 3))

(display (add-three 5)) (newline) ; 8
(display (add-three 12)) (newline) ; 15

Tcl

proc uncurried_add {x y} {
    expr {$x + $y}
}

proc curried_add x {
    list apply [list y [format {expr {%d + $y}} $x]]
}

puts stdout [uncurried_add 3 5]; # 8
puts stdout [{*}[curried_add 3] 5]; # 8

set add_three [curried_add 3]
puts stdout [{*}$add_three 5]; # 8
puts stdout [{*}$add_three 12]; # 15

References and comments

1. ↑ Moses Schönfinkel : About the building blocks of mathematical logic. In: Mathematische Annalen 92 (1928). Pp. 305-316, digitized .
2. ↑ Gottlob Frege : Fundamental laws of arithmetic. Hermann Pohle, Jena 1893 (Volume I) 1903 (Volume II) korpora.org .
3. ↑ Haskell Brooks Curry , Robert Feys, Roger Hindley , Jonathan P. Seldin: Combinatory Logic. North Holland, 2 volumes, 1958, 1972.
4. ↑ This denotes or the set of images from to . ${\displaystyle (X\to Y)}$ ${\displaystyle [X\to Y]}$ ${\displaystyle X}$ ${\displaystyle Y}$
5. ↑ In the zero-digit case (n = 0), the currying would assign a mapping without parameters and with a value to a single-digit mapping with a constant value , for example ${\displaystyle f}$ ${\displaystyle b\in B}$ ${\displaystyle b}$

   ${\displaystyle f_{curried}:B\to B,x\mapsto b}$.

6. ↑ An example is with (where the diagonal denotes). ${\displaystyle f(a_{1},a_{2}):=a_{1}/(a_{1}-a_{2})}$ ${\displaystyle a_{1},a_{2}\in \mathbb {R} \setminus \Delta _{\mathbb {R} }}$ ${\displaystyle \Delta _{\mathbb {R} }}$ ${\displaystyle \{(a_{1},a_{2})\in \mathbb {R} ^{2}|a_{1}=a_{2}\}}$
7. ↑ In the example above, this is . ${\displaystyle \mathbb {R} \setminus \{a_{1}\}}$
8. ↑ The prerequisite is that the symbol is not already overloaded with arity 1 in some other way (see example below, this makes it necessary to distinguish between and ). ${\displaystyle f}$ ${\displaystyle \operatorname {mult} }$ ${\displaystyle \operatorname {prod} }$
9. ↑ To distinguish it from the placeholder , the multiplication sign is used here. ${\displaystyle \cdot }$ ${\displaystyle *}$
10. ↑ This function could also be given its own name:

    ${\displaystyle \operatorname {doppelt} :=\operatorname {mult} _{curried}(2)=\operatorname {mult} (2,\cdot ):\mathbb {N} \to \mathbb {N} }$

    with . ${\displaystyle \operatorname {doppelt} (n)=2*n}$
11. ↑ Distinguish between and the overloaded function with arity and factors . Although it is two-digit , it is a single-digit while is a single-digit function. ${\displaystyle \operatorname {mult} }$ ${\displaystyle \operatorname {prod} }$ ${\displaystyle \operatorname {prod} (k_{1},\cdots ,k_{r})=\prod _{i=1}^{r}k_{i}}$ ${\displaystyle r}$ ${\displaystyle k_{i}\in \mathbb {N} }$ ${\displaystyle \operatorname {mult} (m,n)=\operatorname {prod} (m,n)=m*n}$ ${\displaystyle \operatorname {prod} (m)=m}$ ${\displaystyle \operatorname {mult} (m)=\operatorname {mult} _{curried}(m)=\operatorname {mult} (m,\cdot )}$