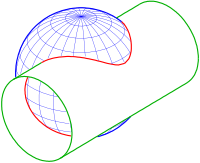
Intersection curve

In the simplest case, an intersection curve is understood to be the intersection of two non-parallel planes of the visual space. In general, the intersection curve of two surfaces consists of the common points at which the surfaces intersect transversely . Transversal means that at every common point the surface normals do not lie on a straight line. With this restriction, one rules out that the surfaces touch one another or even have whole surface areas in common.

Intersection of two planes

The determination of the intersection curve of two surfaces is only possible analytically in simple cases. For example: a) intersection of two planes, b) intersection of a plane with a quadric (sphere, cone, hyperboloid, ...), c) intersection of two quadrics in special positions (e.g. rotation quadrics with the same rotation axis). For more general cases, algorithms are provided in the literature with which one can calculate polygons with points on the intersection curve of two surfaces. For cases that frequently occur in technology (intersection cylinder-sphere, cylinder-cone, ...), the representational geometry offers methods with which individual points of an intersection curve (penetration curve) can be determined graphically. See: auxiliary plane method , swing plane method , surface line method and auxiliary sphere method .

Intersection of two planes

Given: Two levels linearly independent , i.e. i.e., the planes are not parallel. ${\displaystyle \varepsilon _{i}:\quad {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\quad i=1,2,\quad {\vec {n}}_{1},{\vec {n}}_{2}}$

Wanted: A parametric representation of the intersection line. ${\displaystyle {\vec {x}}={\vec {p}}+t{\vec {r}}}$

The direction of the line of intersection results from the cross product of the normal vectors: . A point on the line of intersection is obtained by intersecting the planes with the plane that is to and perpendicular to it. and is found by inserting into the equations of the levels and . ${\displaystyle {\vec {r}}={\vec {n}}_{1}\times {\vec {n}}_{2}}$ ${\displaystyle P:{\vec {p}}}$ ${\displaystyle \varepsilon _{1},\varepsilon _{2}}$ ${\displaystyle \varepsilon _{1}}$ ${\displaystyle \varepsilon _{2}}$ ${\displaystyle \varepsilon _{3}:{\vec {x}}=s_{1}{\vec {n}}_{1}+s_{2}{\vec {n}}_{2}}$ ${\displaystyle s_{1}}$ ${\displaystyle s_{2}}$ ${\displaystyle \varepsilon _{1}}$ ${\displaystyle \varepsilon _{2}}$

${\displaystyle P:{\vec {p}}={\frac {d_{1}{\vec {n}}_{2}^{2}-d_{2}({\vec {n}}_{1}\cdot {\vec {n}}_{2})}{{\vec {n}}_{1}^{2}{\vec {n}}_{2}^{2}-({\vec {n}}_{1}\cdot {\vec {n}}_{2})^{2}}}{\vec {n}}_{1}+{\frac {d_{2}{\vec {n}}_{1}^{2}-d_{1}({\vec {n}}_{1}\cdot {\vec {n}}_{2})}{{\vec {n}}_{1}^{2}{\vec {n}}_{2}^{2}-({\vec {n}}_{1}\cdot {\vec {n}}_{2})^{2}}}{\vec {n}}_{2}\ .}$

Example: ${\displaystyle \varepsilon _{1}:\ x+2y+z=1,\quad \varepsilon _{2}:\ 2x-3y+2z=2\ .}$

The normal vectors are and the direction vector of the intersection line . According to the above formula, So is for the point ${\displaystyle {\vec {n}}_{1}=(1,2,1)^{\top },\ {\vec {n}}_{2}=(2,-3,2)^{\top }}$ ${\displaystyle {\vec {r}}={\vec {n}}_{1}\times {\vec {n}}_{2}=(7,0,-7)^{\top }}$ ${\displaystyle P:{\vec {p}}}$ ${\displaystyle {\vec {p}}={\tfrac {1}{2}}(1,0,1)^{\top }\ .}$

${\displaystyle {\vec {x}}={\tfrac {1}{2}}(1,0,1)^{\top }+t(7,0,-7)^{\top }}$

a parametric representation of the intersection of both planes.

Comment:

1. In the case of specifically specified plane equations , the Gaussian algorithm can also be used to determine a parameter representation of the line of intersection. The above approach is more suitable as a programmable formula for the general case.
2. If a level (or both) in parametric representation is given, obtained by a normal vector and the equation of the plane: . ${\displaystyle {\vec {x}}={\vec {p}}+s{\vec {v}}+t{\vec {w}}}$ ${\displaystyle {\vec {n}}={\vec {v}}\times {\vec {w}}}$ ${\displaystyle {\vec {n}}\cdot {\vec {x}}={\vec {n}}\cdot {\vec {p}}}$

Intersection curve of a plane with a quadric

The intersection curve of a plane with a quadric (sphere, cone, cylinder, ...) is always a conic section. For the analytical determination of the plane sections of a vertical circular cone: see conic section . The plane cuts of other quadrics e.g. B. the plane sections of a sphere, a cylinder, a paraboloid, a hyperboloid can be found here:.

Planar sections of quadrics find an important application in the determination of contour curves. Because both with parallel projection and with central projection, the outlines of quadrics are flat sections. For more general surfaces, contour curves are usually no longer plane cuts. See: Outline construction .

Intersection curve of a cylinder / cone with a quadric

Since determining the point of intersection of a straight line with a quadric in implicit form (e.g. sphere ) only requires the solution of a quadratic equation, any number of intersection points of the intersection curve of a cylinder or cone (both are generated by straight lines) can be calculated with a quadric and visualize it using a polygon (see pictures). ${\displaystyle x^{2}+y^{2}+z^{2}=1}$

The pictures show the possibilities that can occur when a cylinder is intersected with a sphere:

1. In the first picture there is a coherent intersection curve.
2. In the second picture the intersection curve is divided into two separate curves.
3. In the third picture, the cylinder and sphere touch at a point (singular point). Here the surface normals have the same direction. The intersection curve penetrates itself at the point of contact.
4. If the cylinder and sphere have the same radius and the center of the sphere lies on the cylinder axis, the sphere and cylinder touch each other in a circle. The intersection of the two consists exclusively of singular points.

• 

  Intersection curve sphere with a cylinder: 1-part

• 

  Intersection curve sphere with a cylinder: 2 parts

• 

  Intersection curve of a sphere with a cylinder: curve with 1 singularity

• 

  Intersection curve sphere with a cylinder: touching

General case: tracking algorithm

Intersection curve: principle of the tracking algorithm

In the case of more general areas, you cannot take advantage of any special features as above. The tracking algorithm offers one possibility to create a polygon from points of the desired intersection curve (see section Literature ). It consists of two main parts:

1. A curve point algorithm that is dependent on the representation of the surfaces involved and that determines a point on the intersection curve for a point near both surfaces. There is a relatively simple and fast algorithm for implicitly given surfaces, since the functions of the two surfaces can also be evaluated in the vicinity of the surfaces and the gradients of the functions indicate the path to the surfaces involved. Such information is missing for parameterized areas. Here one uses u. a. Algorithms that determine plumb points on surfaces.
2. The second part of the tracking algorithm starts from a known point on the intersection curve and, with the help of the surface normals, determines a tangent to the intersection curve via their cross product. From the first point one then goes by a fixed, predetermined step size in the tangent direction in order to obtain a new starting point for the curve point algorithm. The curve point algorithm delivers the 2nd curve point (see picture).

For details of the tracking algorithm: see.

The tracking algorithm always runs along a contiguous intersection curve. If there are several intersection curves, the algorithm must be run through several times with suitable starting points. In practice, the algorithm is relatively robust. It even runs over individual singularities without any major problems, since it is very unlikely that you will accidentally catch a singular point (see picture with cylinder and surface ). ${\displaystyle x^{4}+y^{4}+z^{4}=1}$

• 

  Intersection curve of the surface with the cylinder: two-part ${\displaystyle x^{4}+y^{4}+z^{4}=1}$

• 

  Intersection curve of the surface with the cylinder: one-piece ${\displaystyle x^{4}+y^{4}+z^{4}=1}$

• 

  Intersection curve of the surface with cylinder: one-piece with sing. Point ${\displaystyle x^{4}+y^{4}+z^{4}=1}$

Application: contour curve

A point of the outline of an implicit surface with the equation must satisfy in the case of a parallel projection in the direction of the condition . I.e. an outline point is a point on the intersection curve of the two implicit surfaces ${\displaystyle (x,y,z)}$ ${\displaystyle f(x,y,z)=0}$ ${\displaystyle {\vec {v}}}$ ${\displaystyle g(x,y,z)=\nabla f(x,y,z)\cdot {\vec {v}}=0}$

${\displaystyle f(x,y,z)=0,\ g(x,y,z)=0}$.

With quadrics, there is always a linear function and thus the contour curve is a plane section. ${\displaystyle g}$

The outline of the area (see picture) was determined and drawn using the tracking algorithm. ${\displaystyle f(x,y,z)=x^{4}+y^{4}+z^{4}-1=0}$

Note: The determination of a contour polygon of a parameterized area requires a polygon to be determined on an implicit curve in the parameter level (see): ${\displaystyle {\vec {x}}={\vec {x}}(s,t)}$

Outline condition: . ${\displaystyle g(s,t)=({\vec {x}}_{s}(s,t)\times {\vec {x}}_{t}(s,t))\cdot {\vec {v}}=0}$

Intersection curves between polyhedra

Intersection curves between polyhedra: 3 houses

Intersection curves between polyhedra: 2 tori

The intersection between two polyhedra is a polygon (see intersection of three houses). Since, in particular, parameterized surfaces are often represented by 4-corner networks and the 4-corner are usually almost flat, the intersection curve results as a section polygon of the individual facets of the surfaces. A suitable algorithm for determining the intersection polygons of two polyhedra can be found here:.

See also

• Intersection
• Positional relationship

Individual evidence

1. ↑ CDKG: Computer-Aided Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 149
2. ↑ CDKG: Computer-assisted Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), pp. 87–124
3. ↑ CDKG: Computer-assisted Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), pp. 153, 158
4. ↑ CDKG: Computer-Aided Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 158
5. ↑ CDKG: Computer-assisted performing and constructive geometry (TU Darmstadt) (PDF; 3.4 MB), p. 179

literature

• C: L: Bajaj, CM Hoffmann, RE Lynch: Tracing surface intersections , Comp. Aided Geom. Design 5 (1988), pp. 285-307.
• RE Barnhill, SN Kersey: AMarching method for parametric surface / surface intersection , Comp. Aided Geom. Design 7 (1990), pp. 257-280.
• R. Barnhill, G. Farin, M. Jordan, B. Piper: Surface / Surface intersection , Computer Aided Geometric Design 4 (1987), pp. 3-16.