Conic section
A conic section (Latin sectio conica , English conic section ) is a curve that is created when the surface of a double cone is intersected with a plane . If the cutting plane contains the tip of the cone, either a point or a straight line or an intersecting pair of straight lines is created as the cut . If the tip is not included, the non-degenerate conic sections ellipse , parabola or hyperbola arise .
The proof that these curves, defined as locus curves in the plane, really arise in the non-degenerate case can be carried out without calculation using Dandelin's spheres . The computational proof is given here in the section Plane Sections of the Unit Cone.
A conic section can also be viewed as a two-dimensional special case of a quadric and can be described by an equation of the 2nd degree, the general conic section equation.
If one embeds the ellipse, hyperbola and parabola in a projective plane, then projective conic sections arise which are all equivalent to one another, i.e. That is, they can be converted into one another using straight-line images.
Equations of conic sections
The conic sections can be described in a suitable xy coordinate system by equations of the 2nd degree:
-
Ellipse with center M at point (0,0) and the main axis on the x-axis:
- (see picture). (For there is a circle.)
-
Parabola with vertex at point (0,0) and the axis on the y-axis:
- (see picture).
-
Hyperbola with center M at point (0,0) and the main axis on the x-axis:
- (see picture).
- To be cut straight couple with the intersection at the point (0,0):
-
Straight through the point (0,0):
-
Point, the point (0,0):
For the sake of completeness, two more cases are added that do not actually appear as conic sections, but are also described by equations of the 2nd degree:
-
Parallel pair of lines:
- The empty set:
- or .
The last two cases can appear as plane sections of a straight circular cylinder . A circular cylinder can be understood as a limiting case of a cone with a cone apex at infinity. Therefore, you take these two cases with you to the conic sections.
Flat sections of the unit cone
In order to determine that the curves / points referred to above as conic sections actually occur when a cone intersects with a plane, here we cut the unit cone (straight circular cone ) with a plane that is parallel to the y-axis. This is not a restriction as the cone is rotationally symmetrical. An arbitrary straight circular cone is the affine image of the unit cone and ellipses / hyperbolas / parabolas / ... merge into the same in an affine image .
Given: plane cone .
Wanted: cut .
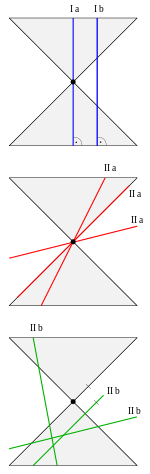
- Case I: In this case the plane is perpendicular and and . If one eliminates from the cone equation, one obtains .
- Case Ia . In this case the section consists of the
- Case Ib . The above equation now describes a hyperbola in the yz plane. So the intersection curve itself is also a hyperbola.
- Case IIa: For the
- For the cut is the
- For (1) turns into and the intersection curve is a parabola.
- For we transform (1) into .
- For the intersection curve is an ellipse and
- for there is a hyperbola.
Parameter representations of the intersection curves can be found in Weblink CDKG, pp. 106-107.
Summary:
- If the cutting plane does not contain the apex of the cone , the non-degenerate conic sections are created (see picture for Ib, IIb), namely a parabola, an ellipse or a hyperbola, depending on whether the cone axis from the cutting plane is below the same, a larger or a smaller one Angle is cut as by the generatrix of the cone.
- If, on the other hand, the apex of the cone lies in the cutting plane, the degenerate conic sections arise (see figure for Ia, IIa), namely a point (namely the apex of the cone), a straight line (namely a surface line) or an intersecting pair of straight lines (namely two surface lines) .
General conic equation
The general equation for conic sections is
-
- (note that parameters a and b are not those of the previous section)
In particular, the parameters are not all 0. If is, the equation describes a straight line or a whole .
It should now be shown that only the above 8 cases occur as solution sets of the general conic section equation. We achieve the goal in two essential steps, the main axis transformation :
- Rotation of the coordinate system to remove the term .
- Shifting the zero point (translation) so that the linear terms disappear as far as possible .
Step 1: If so, we do the rotation
- around the angle with or , if , through.
The conic section equation then has the form
- (instead of being used again ).
2nd step:
- If is a leading completing the square to the term and thus to shift .
- If is a square supplement leads to the term and thus to shift .
After these two steps the conic section equation (x 'and y' are again replaced by x, y) finally has the form
- I: with or
- II: or with .
Only the above 8 cases can occur:
- In case I there is an ellipse or a hyperbola or the empty set, if is, or a point or an intersecting pair of lines, if is.
- In case II a parabola results , if is, or a parallel pair of lines or a straight line or the empty set, if is.
The transformations carried out here (rotation, displacement) do not change the geometric shape of the conic section described by the original equation. Parameters such as semi-axes for ellipses and hyperbola or focal length for the parabola or angle / distance between intersecting / parallel straight lines can be read from the transformed conic section.
Note: The quadratic part of the general conic section equation can also be written with the help of a 2 × 2 matrix :
Since a rotation and a shift does not change the sign of the determinant of the 2 × 2 matrix, leads to case I and case II. If you know that the original conic section equation represents a conic section that has not degenerated, you can already see from the determinant whether it is an ellipse ( ) or a hyperbola ( ) or a parabola ( ).
Comment:
- Since the general conic section equation is only determined by the 6 coefficients up to one factor, 5 points (equations) are required to determine the coefficients . But: Not every choice of 5 points clearly defines a conic section. (Counterexample: 4 points on a straight line, 1 point not on the straight line.) A non-degenerate conic section (ellipse, hyperbola, parabola) is clearly defined by 5 points, with no 3 on a straight line. An elegant formula for the undeveloped case uses a 6 × 6 determinant :
- ( are the given points. See.)
- A circle is clearly defined by 3 points (not on a straight line). The equation is obtained from the 4 × 4 determinant
- .
Example: The cone section of the 5 points is above according to calculate determinant equation or after simplification . The main axis transformation takes place with a rotation of . A shift is not necessary. The conic section has the transformed equation and is an ellipse.
Vertex equation of a family of conics
The family of non-degenerate conic sections whose axis is the -axis and which have a vertex at point (0,0) can be given by the equation
describe (for evidence see guideline property of the hyperbola ). For
- you get a circle,
- for an ellipse,
- for a parabola and
- for a hyperbola.
is the numerical eccentricity.
- is the width of the conic section measured at the focal point perpendicular to the axis.
- is the vertex curvature radius in the vertex .
- For ellipses and hyperbolas , where is the semi-major axis and the linear eccentricity . In the case of an ellipse, the center is and a focal point. In the case of a hyperbola is the center and a focal point. In the case of a parabola, the focus is. For the circle (with ) the center is at and the radius is .
Polar equation of a family of conics
The guideline property of the non-degenerate conics is:
- The set of points of the Euclidean plane whose distances to a given straight line and a given point satisfy the condition is constant is an ellipse, if , a parabola, if , a hyperbola, if is.
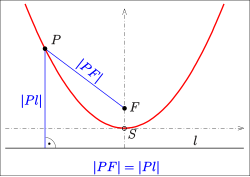
If the point is the zero point and the straight line has the equation , the following applies in polar coordinates (see figure):
Resolve for supplies first . If one sets , one obtains the polar representation of the non-degenerate conic sections:
- .
is the half parameter (half the width of the conic section at the focal point) and the numerical eccentricity. If you choose the half-parameter fixed, you get conic sections with the zero point as the common focal point, namely
- for the circle with center and radius ,
- for the ellipse with the center point and the semi-axes ,
- for the parabola with the vertex and the equation ,
- for the hyperbola with the center and the semi-axes .
Conic section tufts
If the equations of two conic sections are given, the linear combination
of the equations generate new conic sections. Since proportional pairs and equivalent equations result and therefore belong to the same conic section, the linear combination is often written as:
This equation unambiguously describes a conic section through the parameter .
Example of circular tufts:
For the two circular equations
describes with a cluster of circles (see picture). (For the quadratic terms cancel each other out and the straight line results .)
Example of a conic section through 2 points with specified tangents:
The following example builds a cluster of conic sections from 3 straight lines . Let it be:
Then describe the equation
with the family parameter a tuft of conic sections through the two points and . Each conic section touches the two straight lines at these points. The conic section tuft is thus determined by the two points and the two tangents at these points. ( A conic section is always clearly defined by 5 specifications!) Both conics, with which the linear combination is formed, are degenerate conics ( is a pair of straight lines and is a double straight line ).
Example of a conic section through 4 points:
In this case the tuft is a linear combination of two parallel pairs of lines that intersect at the 4 points (see picture):
Exactly one (possibly degenerate) conic section of the tuft goes through every point of the plane that is different from the base points of the tuft. For example, the zero point for the pair of lines is obtained .
Conic section tufts are extensively studied in the literature.
Equivalence of non-degenerate conic sections
- All ellipses are affine images of the unit circle (see ellipse ).
- All parabolas are affine images of the normal parabola (see parabola ).
- All hyperbolas are affine images of the unit hyperbola (see hyperbola ).
However, an ellipse can not (e.g.) be mapped onto a parabola with an affine mapping . If, however, the affine coordinate plane is added to a projective plane and the far point of its axis is added to a parabola, an ellipse with a projective mapping can be mapped onto such an extended parabola. The same applies to a hyperbola supplemented by the two far points of its asymptotes.
- From the projective point of view, all non-degenerate projective conic sections are equivalent to one another (see also CDKG web link, p. 251).
Examples:
- The projective mapping with maps the unit circle onto the parabola .
- The projective mapping with maps the parabola onto the hyperbola .
Applications and examples

The conic sections are used in astronomy , as the orbits of the celestial bodies are approximated conic sections.
They are also used in optics - as an ellipsoid of rotation for car headlights , as a paraboloid or hyperboloid for reflector telescopes , etc.
In descriptive geometry , conic sections appear as images of circles in parallel and central projections. See Ellipse (Descriptive Geometry) .
history
The Greek mathematician Menaichmos examined the conic sections at Plato's academy with the help of a cone model. He found out that the Delian problem can be traced back to the determination of the intersection of two conic sections. After that, Aristaios of Samos (Aristaios the Elder) dealt with the problem of the construction of conic sections in relation to three or four straight lines in a no longer extant book, which was later taken up again in the reasoning of the analytical geometry by René Descartes . Euclid wrote four books on conic sections, but they have not survived. Apollonios von Perge summarized the entire knowledge of the ancient mathematicians about the conic sections in his eight-volume work Konika , whereby Apollonios like Euclid preferred the synthetic approach to geometry. The works of Euclid, Apollonios and Aristaios were taken up and further developed in Western Europe from the Renaissance onwards. The description of conic sections by coordinate equations was introduced by Fermat and Descartes.
Conic sections over any number fields
Conic sections can also be defined over any bodies . A surprising number of incidence and symmetry properties are retained. See web link Projective Geometry, Projective Conics and for Conics over finite bodies the article Quadratic Set .
Conics and Benz planes
Conic sections play an important role in the Benz planes , i.e. Möbius planes (geometry of circles), Laguerre planes (geometry of parabolas) and Minkowski planes (geometry of hyperbolas).
See also
- Conic sections as rational Bezier curves
- Confocal conic sections
- Focal conic section
- Basket arch , celestial mechanics , two-body problem , projective geometry , rotating quadric , collection of formulas for analytical geometry .
Web links
- Conic sections. ( Memento of March 5, 2016 in the Internet Archive ). University of Vienna.
- Projective geometry. Short script. Darmstadt University (PDF; 180 kB), pp. 12–16.
- Computer-aided performing and constructive geometry. (CDKG) University of Darmstadt (PDF; 3.4 MB).
- Apollonius von Perga's seven books on conic sections.
- J. Casey: A treatise on the analytical geometry of the point, line, circle and conic sections. 1893.
- A. Coffman: Linear Systems of Conics.
literature
- Max Koecher , Aloys Krieg : level geometry. 3rd edition, Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3 .
- Burg, Haf, Wille: Higher Mathematics for Engineers. Volume II, Teubner-Verlag Stuttgart, ISBN 3-519-22956-0 , p. 338.
supporting documents
- ↑ Small Encyclopedia of Mathematics. VEB Verlag Enzyklopädie, Leipzig, 1977, p. 325 f.
- ^ Meyberg & Vachenauer: Higher Mathematics 1. Springer-Verlag, Berlin, ISBN 3-540-59188-5 , p. 309.
- ↑ For example, Barry Spain: Analytical Conics. Dover Publications, 2007, ISBN 0-486-45773-7 , p. 91.
- ↑ Projective geometry. Short script, Uni Darmstadt (PDF; 180 kB), p. 12.