Projective plane

In geometry, a projective plane is an incidence structure comprising points and lines . A projective plane over a body consists of the 1-dimensional subspaces of the 3-dimensional vector space as points and the 2-dimensional subspaces of as straight lines. In abstract terms, projective planes can essentially be characterized by two requirements (axioms), namely that every two straight lines have a (unambiguous) intersection and every two points have a (unambiguous) connecting straight line . Since these requirements are very weak, there are many examples that meet them. Only through further restrictions, e.g. B. Using Desargues ' theorem , one obtains algebraically well describable examples whose properties are examined in the context of projective geometry . In addition to projective planes, there are also projective spaces , as in affine geometry . ${\displaystyle K}$ ${\displaystyle K^{3}}$ ${\displaystyle K^{3}}$

motivation

Theorems on the geometry of the (affine) plane known from school, in which straight lines occur, must almost always differentiate in their formulation between parallel and intersecting straight lines. The construction of the projective plane is intended to expand the affine plane in such a way that this distinction is no longer necessary because all straight lines intersect. For this purpose, one takes points at infinity as intersection points of parallel lines to the plane, namely one point at infinity for any set of parallel lines (in any direction).

This can be realized mathematically as follows. The affine plane is embedded using ${\displaystyle \mathbb {R} ^{2}}$

${\displaystyle j\colon \mathbb {R} ^{2}\to \mathbb {R} ^{3},(x,y)\mapsto (x,y,1)}$

into the 3-dimensional Euclidean space . Then there is a unique straight line through the origin (straight line through the zero point) through each point of the image plane . However, not all straight lines through the origin intersect the image plane, namely the straight lines lying in the plane do not. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \left\{(x,y,0)\in \mathbb {R} ^{3}\right\}}$

Now the points at infinity should correspond to the sets of parallel straight lines im and these in turn correspond uniquely to the straight lines through the origin im (each straight line is parallel to a unique straight line through the origin ) or, which is the same, in . So we establish that the points at infinity clearly correspond to the straight line through the origin lying in the plane and the points in or, which is the same thing, in the plane clearly correspond to the straight line through the origin not lying in the plane . ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \left\{(x,y,0)\in \mathbb {R} ^{3}\right\}}$ ${\displaystyle \left\{(x,y,0)\in \mathbb {R} ^{3}\right\}}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \left\{(x,y,1)\in \mathbb {R} ^{3}\right\}}$ ${\displaystyle \left\{(x,y,0)\in \mathbb {R} ^{3}\right\}}$

This results in the definition of the (real) projective plane as a set of straight lines through the origin im . The projective plane defined in this way contains both the affine plane and the points at infinity (equivalence classes of parallel straight lines) of the plane. (An analogous definition can be carried out for arbitrary bodies instead .) ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle K}$ ${\displaystyle \mathbb {R} }$

Formally, this can be defined as , where two vectors are considered equivalent if they are linearly dependent, i.e. if they are true for a real number . The point of the projective plane corresponding to a point is noted . It then applies ${\displaystyle (\mathbb {R} ^{3}\setminus \left\{(0,0,0)\right\})/\sim }$ ${\displaystyle v_{1},v_{2}\in \mathbb {R} ^{3}\setminus \left\{(0,0,0)\right\}}$ ${\displaystyle v_{2}=kv_{1}}$ ${\displaystyle k}$ ${\displaystyle (x,y,z)\in \mathbb {R} ^{3}}$ ${\displaystyle \left[x:y:z\right]}$

${\displaystyle \left[kx:ky:kz\right]=\left[x:y:z\right]}$

for everyone . There is no point because no straight line through the origin is defined. ${\displaystyle k\in \mathbb {R} \setminus \left\{0\right\}}$ ${\displaystyle \left[0:0:0\right]}$ ${\displaystyle (0,0,0)}$

The points of the projective plane thus correspond to the straight lines through the origin im , the straight lines of the projective plane correspond to the original planes im . One can show that every two (different) straight lines of the projective plane intersect at exactly one point (and that there is exactly one straight line running through these points for every two different points of the projective plane). The special role of parallel straight lines existing in the affine plane is thus canceled out in the projective plane, all points and straight lines have equal rights. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} ^{3}}$

Projective plane over a body

It is a body . The projective plane is the set of all straight lines through the zero point im . Formally, this is defined as follows. ${\displaystyle K}$ ${\displaystyle KP^{2}}$ ${\displaystyle K^{3}}$

To be the equivalence relation ${\displaystyle K^{3}\setminus \{0\}}$

${\displaystyle x\sim y\Leftrightarrow \exists \lambda \in K\setminus \{0\}\colon x=\lambda y}$

Are defined. In words this means that if and only if there is a such that it is equivalent to . All points on a straight line through the origin - the origin is not included - are therefore identified with one another and no longer differentiated. The quotient space is called the projective plane and is also noted. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \lambda \in K^{*}:=K\setminus \{0\}}$ ${\displaystyle x=\lambda y}$ ${\displaystyle \left(K^{3}\setminus \{0\}\right)/\sim }$ ${\displaystyle KP^{2}}$

Straight lines correspond to points of the projective plane, planes correspond to straight lines to the projective plane. Points and straight lines of the projective plane form an incidence structure . For every two points there is a clear straight line , for every two straight lines there is a clear intersection point. ${\displaystyle K^{3}}$ ${\displaystyle K^{3}}$ ${\displaystyle x,y\in KP^{2}}$ ${\displaystyle {\overline {xy}}}$

If the body is clear from the context, the projective level is often just referred to as or . ${\displaystyle K}$ ${\displaystyle P^{2}}$ ${\displaystyle P}$

Homogeneous coordinates

Every point of the projective plane can be in homogeneous coordinates as

${\displaystyle \left[x:y:z\right]}$

with be shown with all true and this representation is but clearly otherwise. ${\displaystyle x,y,z\in K,(x,y,z)\not =(0,0,0)}$ ${\displaystyle \left[x:y:z\right]=\left[\lambda x:\lambda y:\lambda z\right]}$ ${\displaystyle \lambda \in K\setminus \{0\}}$

Especially in infinity

The affine plane sits naturally in the projective plane as a set of all 1-dimensional subspaces that are not contained in the xy plane, i.e. as ${\displaystyle K^{2}}$

${\displaystyle K^{2}\cong \left\{\left[x:y:1\right]\in KP^{2}\right\}}$.

Its complement forms the so-called projective straight line at infinity

${\displaystyle KP^{1}\cong \left\{\left[x:y:0\right]\in KP^{2}\right\}}$.

Similarly, one can also construct a decomposition for every other 2-dimensional subspace . The corresponding subset is called the affine map . ${\displaystyle E\subset K^{3}}$ ${\displaystyle KP^{2}=E\cup P(E)}$ ${\displaystyle E\subset KP^{2}}$

Automorphisms

The group of projective transformations is the projective linear group . For every two ordered 4-tuples of points in there is an unambiguous projective transformation which converts one 4-tuple into the other. ${\displaystyle \operatorname {PGL} (3,K)}$ ${\displaystyle KP^{2}}$

In the case one has an isomorphism . ${\displaystyle K=\mathbb {R} }$ ${\displaystyle \operatorname {PGL} (3,\mathbb {R} )=\operatorname {SL} (3,\mathbb {R} )}$

Dual level

For a firmly chosen body we denote the space of the straight lines in the projective plane (i.e. the 2-dimensional subspaces in ). The incidence relation assigns two straight lines to their clear intersection. ${\displaystyle K}$ ${\displaystyle P^{*}}$ ${\displaystyle P}$ ${\displaystyle K^{3}}$ ${\displaystyle P^{*}}$

A duality mapping is a projective-linear mapping of on , i.e. a homeomorphism that maps collinear points onto intersecting straight lines. Every duality induces a dual mapping by means of . A duality mapping swaps the terms “point” and “straight line” in : It maps points from to points in , that is, straight lines in , and is compatible with the incidence relations. ${\displaystyle P}$ ${\displaystyle P^{*}}$ ${\displaystyle \Delta \colon P\to P^{*}}$ ${\displaystyle \Delta ^{*}\colon P^{*}\to P}$ ${\displaystyle \Delta ^{*}({\overline {pq}})=\Delta (p)\cap \Delta (q)}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle P^{*}}$ ${\displaystyle P}$

A polarity is one of a scalar product on induced duality Figure: Each 1-dimensional sub-space is arranged with respect to the scalar orthogonal 2-dimensional sub-space. To this defines a mapping . ${\displaystyle K^{3}}$ ${\displaystyle l\subset K^{3}}$ ${\displaystyle e\subset K^{3}}$ ${\displaystyle \Delta \colon P\to P^{*}}$

Projective planes in topology, differential geometry and finite geometry

Real projective plane

The real projective plane as the quotient set of a sphere

In some respects, especially as far as the topology is concerned, one can understand a real projective plane as what one obtains when one has antipodes on a sphere (surface of a sphere in 3-dimensional space), i.e. points of the sphere that are on both Ends of a diameter are "equated". To put it more precisely, this means that the points of the projective plane are each pair of antipodes and the straight lines of them are the great circles, i.e. the circles that intersect the sphere with an ordinary plane passing through the center of the sphere. The real projective plane thus also becomes topologically the quotient topology of the sphere.

The projective tangential bundle of the projective plane is the plume manifold ${\displaystyle P(T\mathbb {R} P^{2})}$ ${\displaystyle P=\mathbb {R} P^{2}}$

${\displaystyle \operatorname {Flag} (R^{3})=\left\{(l,e)\in P\times P^{*}\colon l\in e\right\}}$.

By means of the polarity defined by a scalar product, one can understand planes in as 1-forms and then also define the projective tangential bundle as ${\displaystyle V=\mathbb {R} ^{3}}$ ${\displaystyle e\in P(V^{*})}$

${\displaystyle \operatorname {Flag} (\mathbb {R} ^{3})=\left\{(l,e)\in P(V)\times P(V^{*})\colon e(l)=0\right\}}$.

The real projective plane as a non-orientable surface

The specified identification of the sides gives the real projective plane.

The sphere itself is an orientable surface ; it is no longer the projective plane resulting from this process of quotient formation, since the antipodal image, as a reflection around the center point, is not a rotation and is therefore not an orientation-preserving image.

The real projective plane (in this context usually just referred to as the projective plane ) is the simplest example of a non-orientable surface, it is the non-orientable surface of gender 1. Every other non-orientable surface is obtained as a connected sum of one ( in this context also referred to as cross hood ) projective plane or two projective planes with a number of tori, or also equivalently as a coherent sum of projective planes - this follows from the classification of the surfaces and the identity . ${\displaystyle T^{2}\sharp \mathbb {R} P^{2}=\mathbb {R} P^{2}\sharp \mathbb {R} P^{2}\sharp \mathbb {R} P^{2}}$

The decomposition provides a decomposition of as a CW complex with one cell each in dimensions 2,1,0. With this decomposition, the homology groups can be calculated, one obtains: ${\displaystyle \mathbb {R} P^{2}=\mathbb {R} ^{2}\cup P(\mathbb {R} ^{2})=\mathbb {R} ^{2}\cup \mathbb {R} P^{1}=\mathbb {R} ^{2}\cup \mathbb {R} ^{1}\cup \mathbb {R} ^{0}}$ ${\displaystyle \mathbb {R} P^{2}}$

${\displaystyle H_{0}(\mathbb {R} P^{2})=\mathbb {Z} ,H_{1}(\mathbb {R} P^{2})=\mathbb {Z} /2\mathbb {Z} ,H_{2}(\mathbb {R} P^{2})=0}$.

Immersions of the real projective plane in 3-dimensional space

Bryant-Kusner parameterization of the Boy surface

The real projective plane can be represented as a surface in three-dimensional space. Examples of this are the Boy area and the Roman area . Exactly as with the likewise non-orientable Klein bottle, it is not possible to embed the projective plane in the three-dimensional space without self-penetration.

Among the immersions of the projective plane in the , the Bryant-Kusner parameterization realizes the immersion of minimal Willmore energy . ${\displaystyle \mathbb {R} ^{3}}$

Complex projective plane

The complex projective plane is fundamental in algebraic geometry and algebraic topology.

Subsets defined by a homogeneous polynomial ${\displaystyle P\in \mathbb {C} \left[x,y,z\right]}$

${\displaystyle V(P)=\left\{\left[x:y:z\right]\in \mathbb {C} P^{2}\colon P(x,y,z)=0\right\}}$

are called algebraic curves , they are Riemann surfaces and the simplest examples of algebraic varieties .

The decomposition yields a decomposition of as a CW complex with one cell each in dimensions 4,2,0. With this decomposition, the homology groups can be calculated, one obtains: ${\displaystyle \mathbb {C} P^{2}=\mathbb {C} ^{2}\cup P(\mathbb {C} ^{2})=\mathbb {C} ^{2}\cup \mathbb {C} P^{1}=\mathbb {C} ^{2}\cup \mathbb {C} ^{1}\cup \mathbb {C} ^{0}}$ ${\displaystyle \mathbb {C} P^{2}}$

${\displaystyle H_{0}(\mathbb {C} P^{2})=\mathbb {Z} ,H_{1}(\mathbb {C} P^{2})=0,H_{2}(\mathbb {C} P^{2})=\mathbb {Z} ,H_{3}(\mathbb {C} P^{2})=0,H_{4}(\mathbb {C} P^{2})=\mathbb {Z} }$.

The second homology group is isomorphic to the integers and the homologue class defined by a smooth algebraic curve corresponds to the degree of the defining polynomial under this isomorphism. Is the gender of a Riemann surface defined by a polynomial of degree . The Thom conjecture , proven by the Seiberg-Witten theory , states that algebraic curves are the surfaces of minimal gender in their homology classes. ${\displaystyle H_{2}(\mathbb {C} P^{2})}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle d}$ ${\displaystyle g={\frac {1}{2}}(d-1)(d-2)}$

The complex projective plane is important in cobordism theory and the theory of characteristic classes . The following applies to the orientable cobordism ring ${\displaystyle \Omega _{*}^{SO}}$

${\displaystyle \Omega _{*}^{SO}\otimes \mathbb {Q} =\mathbb {Q} \left[\mathbb {C} P^{2i}\colon i\geq 1\right]}$,

in particular, the 4-dimensional oriented cobordism group of is generated. ${\displaystyle \mathbb {C} P^{2}}$

The Hopf fiber realizes the complex projective plane as the basis of a fiber bundle

${\displaystyle S^{1}\to S^{5}\to \mathbb {C} P^{2}}$.

The complex projective plane is a homogeneous space and even a Hermitian symmetrical space with the Fubini Study metric . The Kähler form of this metric is . The section curvature fulfills the inequality , the maximum section curvature of complex subspaces and the minimum section curvature of totally real subspaces is realized. ${\displaystyle U(3)/(U(1)\times U(2))}$ ${\displaystyle \omega =i\partial {\overline {\partial }}\log |\mathbf {Z} |^{2}}$ ${\displaystyle 1\leq K\leq 4}$ ${\displaystyle \mathbb {C} P^{1}\subset \mathbb {C} P^{2}}$ ${\displaystyle \mathbb {R} P^{2}\subset \mathbb {C} P^{2}}$

Projective plane over a finite body

Let it be a finite body with elements, then the projective plane has points and just as many straight lines. Every straight line has points and every point lies on straight lines. The projective level above is therefore a 2 - block plan . ${\displaystyle F_{q}}$ ${\displaystyle q}$ ${\displaystyle q^{2}+q+1}$ ${\displaystyle q+1}$ ${\displaystyle q+1}$ ${\displaystyle F_{q}}$ ${\displaystyle (q^{2}+q+1,q+1,1)}$

An example is the Fano level that you get for . ${\displaystyle q=2}$

Projective levels as an incidence structure

definition

An incidence structure is called a projective level if:

• For every two different points there is exactly one straight line that intersects with both.
• For every two different straight lines there is exactly one point that incides with both.
• There is a complete quadrilateral ; H. four points, no three of which incise with the same straight line.

Examples

The minimal model of a projective plane: the Fano plane

• If one understands the two-dimensional subspaces as straight lines and the one-dimensional subspaces as points in the three-dimensional vector spaces above the real numbers or the complex numbers , one obtains models of a projective plane. The incidence relation is the usual inclusion . These levels together with the similarly obtained levels above the quaternions or the octonions are also referred to as classical levels . Instead of real or complex numbers, you can use any field , even an oblique field like the quaternions. ${\displaystyle \subseteq }$ ${\displaystyle K}$
• A projective plane can be realized as a projective plane over a body if and only if Pappus' theorem applies to it.
• A projective plane can be realized as a projective plane over an inclined body if and only if Desargues' theorem applies to it. Such projective planes over oblique bodies are therefore called desarguean projective planes .
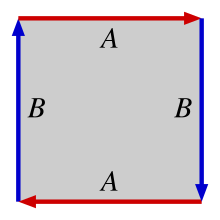
• The smallest possible finite projective plane (minimal model) consists of seven straight lines and seven points (see fig.). In this case, the field that only consists of the 0 and the 1 and in which 1 + 1 = 0 is the remainder class field . ${\displaystyle K}$ ${\displaystyle \mathbb {F} _{2}}$
• There are also non-Desargue projective planes . They can be coordinated by (finite or infinite) ternary bodies in a similar way as the desarguesses by oblique bodies. → See also classification of projective planes .

Remarks

Principle of duality

One can show that there are always four straight lines in a projective plane, none of which go through the same point. From this and from the symmetrical formulation of the first two axioms it can be seen that by exchanging the terms point and straight line, a projective plane is obtained again. The points and lines of form the lines and points of the plane to be dual . The principle of duality is the fact that universal statements about projective levels remain correct even if the roles of points and lines are reversed in their formulations. ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle {\mathfrak {P}}^{\star }}$

Connection with affine planes

If one adds a further improper point to an affine plane for each family of parallel straight lines , which is supposed to incise with exactly the straight lines of its family, and if one extends by the improper straight line that contains exactly these points, then one gets a projective plane, the projective completion of . Conversely, an affine part of a projective plane is obtained by deleting an arbitrary straight line with all its points. It should be noted: ${\displaystyle {\mathfrak {A}}=\langle P,{\mathcal {L}},{\textbf {F}}\rangle }$ ${\displaystyle P}$ ${\displaystyle {\mathcal {L}}}$ ${\displaystyle W}$ ${\displaystyle {\overline {\mathfrak {A}}}}$ ${\displaystyle {\mathfrak {A}}}$ ${\displaystyle {\mathfrak {P}}^{W}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle W}$

1. The affine planes created by deleting two different straight lines from a projective plane do not have to be isomorphic to one another.
2. In particular, the termination of an affine plane by a distant line and subsequent deletion of another straight line (also called slitting along a straight line ) in the projective plane thus formed always provides a new affine plane, which is not necessarily isomorphic to the original affine plane.

The projective planes, in which all the slotted sections are isomorphic affine planes to one another, are precisely the Moufan planes .

Finite projective planes

As the minimal model described above shows, projective planes can be finite, that is, they can only contain a finite number of points and lines. If a straight line contains points, then all straight lines contain points, straight lines pass through each point and, in total, there are straight lines and points. in this case is called the order of the plane. A finite projective plane of order can be combinatorially as a symmetrical - block plan conceived. The smallest possible order of a finite projective plane is two. For every order that is a prime power , a finite projective plane can be constructed as a projective plane over the finite field of the corresponding order. Whether there is such a level, the order of which is not a prime power, is an unsolved problem. Partial results: The non-existence of a projective plane of order 10 was proven with great use of computers. The Bruck-Ryser-Chowla theorem says: If the order is a projective plane or , then is the sum of two whole square numbers. According to this, there are no projective levels of orders 6, 14, 21, 22, 30, 33, 38, 42, 46, ... Whether there are those of orders 12, 15, 18, 20, 24, 28, ... there is unknown. ${\displaystyle n+1}$ ${\displaystyle n+1}$ ${\displaystyle n+1}$ ${\displaystyle n^{2}+n+1}$ ${\displaystyle n^{2}+n+1}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle 2-\left(n^{2}+n+1,n+1,1\right)}$ ${\displaystyle p^{n}\,(n\geq 1)}$ ${\displaystyle n=4k+1}$ ${\displaystyle 4k+2}$ ${\displaystyle n}$

A special class of finite projective planes of order n can be completely described by a set of only natural numbers: the planes that are derived from a set of differences . It is known that every desargue finite level belongs to this class and it is assumed that every level of this class is desargue. ${\displaystyle n+1}$

classification

Closure rates

Obvious is a classification of the projective planes purely based on the concept of incidence. This is done by determining whether certain geometric propositions of the form "if a certain configuration of incidences is present, another incidence also applies" in a plane. Examples of such inference clauses are the theorems of Desargues and Pappos (sometimes also called Pappos-Pascal theorem ) known from the real plane (and valid there ). Levels in which the above sentences apply are called Desarguessian or Papposian levels . A level in which Desargues' little projective theorem is generally valid is called the Moufang level . Every Papposian level is desargue and every desargue is a Moufang level.

Coordination

→ Main article : Ternary bodies

Another common method in geometry is the introduction of coordinates to make algebraic methods useful . These establish a connection between the geometrical structure of the plane and the algebraic structure of an underlying coordinate range. Coordinates can be introduced in every projective plane: For this purpose, a projective point base is selected in the plane, which defines a straight line to the distance line (→ see projective coordinate system ). Then a ternary body with a ternary link , which can be described purely geometrically, can be constructed as a set of coordinates on the affine plane, which is created by cutting out this long line . The calculation rules in a body do not generally apply in the associated coordinate area, the ternary body.

There is a direct relationship between the geometric structure of the plane and the algebraic structure of the coordinate range, which characterizes the planes in a certain way. The Moufang levels are z. B. Exactly the projective planes whose coordinate area is an alternative body , the Desarguessian planes are exactly those that have a sloping body as a coordinate area. If the coordinate area is a commutative body , then the plane is Papposian. In this case, homogeneous coordinates are mostly used (→ see the main article Homogeneous coordinates ). From Wedderburn's theorem it follows that finite Desarguean planes are always papposian. Ruth Moufang succeeded in proving that even every finite Moufang plane is papposian.

Collineations

→ Main article : Classification of projective planes

The straight bijjections are the structure-preserving images (or isomorphisms ) between projective planes. Such a bijection maps the points onto the points and the straight lines onto the straight lines in such a way that the incidence is retained. The collineations , that is, the true-to-the-line bijections of a projective plane onto itself, form a group , the so-called collineation group of the plane. Examples of collineations that operate in the slotted projective plane, that is, as affine collineations , are translations or rotations and, more generally, affinities .

On the projective level itself, the group of projectivities is a subgroup of the collineation group. This subgroup is defined in synthetic geometry as the product of the subset of perspectivities in the collineation group. The study of the operations of certain subgroups of the collineation group on the plane is another way of classification.

literature

• David Hilbert , Stefan Cohn-Vossen : Descriptive Geometry . Springer, Berlin a. a. 1932.
• Anatole Katok ; Vaughn Climenhaga: Lectures on surfaces. (Almost) everything you wanted to know about them. Student Mathematical Library, 46th American Mathematical Society, Providence, RI; Mathematics Advanced Study Semesters, University Park, PA, 2008. ISBN 978-0-8218-4679-7
• Jean Gallier; Dianna Xu: A guide to the classification theorem for compact surfaces. Geometry and Computing, 9. Springer, Heidelberg, 2013. ISBN 978-3-642-34363-6 ; 978-3-642-34364-3
• Günter Pickert : Projective levels . 2nd Edition. Springer, Berlin a. a. 1975, ISBN 3-540-07280-2 .
• Daniel R. Hughes, Fred C. Piper: Projective Planes . Springer, Berlin a. a. 1973, ISBN 3-540-90044-6 .
• Hanfried Lenz : Lectures on projective geometry . Geest & Portig, Leipzig 1965.
• Wendelin Degen and Lothar Profke: Fundamentals of affine and Euclidean geometry , Teubner, Stuttgart, 1976, ISBN 3-519-02751-8
• Peter Dembowski : Finite geometries . Springer, Berlin a. a. 1968.
• Helmut Salzmann et al .: Compact projective planes . de Gruyter, Berlin a. a. 1995, ISBN 3-11-011480-1 .

Web links

• The real projective level (Duco van Straten, Oliver Labs, Uni Mainz)
• Survey of Non-Desarguesian Planes (Charles Weibel, Notices of the AMS 2007)
• Projective Planes (Marshall Hall, Transactions of the AMS 1943)

Individual evidence

1. ↑ CWHLam: The Search for a Finite Projective Plane of Order 10