Fano level
The Fano plane (after the Italian mathematician Gino Fano ) is an incidence structure that can be understood as a linear space as well as a projective plane , two-dimensional projective space or a block plan .
In synthetic geometry it is the minimal model of a projective plane. Its affine section, which is created by cutting out a projective straight line, is the minimal model of an affine plane .
The automorphism group of the Fano plane is the group of its projectivities , symbolically represented as , since it is formally a factor group of the general linear group , in fact it is isomorphic to this . is a simple group and is one of the smallest non-commutative simple groups in the classification of finite simple groups. There she is one of the Lie-type groups .
In addition, those projective or (less often) affine planes in which the Fano axiom applies are called Fano planes in the linguistic usage of synthetic geometry . The Fano plane, as described in this article, is not a Fano plane in this axiomatic sense , because it does not satisfy the projective Fano axiom.
Definitions
Visualization, definition as hypergraph
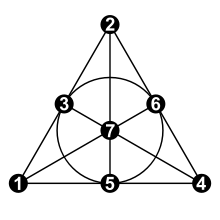
The Fano plane can be visualized and defined by drawing an equilateral triangle with heights and an inscribed circle (first figure above). The 7 elements of , the points , are the three corner points, the three height base points and the center of the inscribed circle. The 7 elements of , the straight lines , are the sides of the triangle, the heights and the inscribed circle. It follows from Sylvester-Gallai's theorem that there is no representation in which all straight lines are actually straight lines of the Euclidean plane. In terms of graph theory , this image can be viewed as a hypergraph with nodes (the points) and edges (the lines and the inscribed circle) and thus as a model of the Fano plane.
Concrete, enumerating definition as incidence structure
The following (symmetrical) incidence structure is called the Fano plane :
- Set of points: or
- Set of straight lines: or
- Incidence relation : applies to and
In this concrete definition by listing the 7 “binary” point symbols (compare the figure on the right: etc.) can simply be taken as idiosyncratic symbols for 7 different points. In fact, they are short for coordinate triples, as explained below. The second, more compact representation of the number of points and lines is created by interpreting these point symbols as numbers in the dual system and converting them into the decimal system .
Definition as projective space
Equivalent to the language of linear algebra , the Fano plane can be defined as the two-dimensional projective space over the finite body with two elements . This field in turn can be modeled by the remainder class field .
Equivalence of Definitions
In terms of synthetic geometry, the Fano plane is a finite projective plane of order 2 with 7 straight lines and 7 points, its symbolic abbreviation is . In the case of the axiomatic description of projective levels, this is obtained by checking the validity of the axioms directly on the basis of the specifically defined incidence structure.
When defining a two-dimensional projective space above the body , one considers the vector space , whose one-dimensional subspaces are then the points of the projective plane, its two-dimensional subspaces are the straight lines and the incidence relation is the set-theoretical subset relation " ". Thus one obtains (formally)
- as a point set: and
- as a straight Quantity: .
The symbols stand for the linear subspaces of the generated by the vector or vectors . The condition in the definition of the set of lines is equivalent for this vector space to the linear independence of the two vectors as long as the zero vector is excluded.
Point coordinates
Now, in the visualized model (equilateral triangle with heights and inscribed circle), a complete quadrilateral , i.e. an ordered, four-element set of points , in which no three points lie on a straight line, can be selected as the projective point base and these points in the given order the (products of ) Assign the standard basis of the plus unit point: etc. - formally more precisely: because the projective point corresponds to a one-dimensional subspace, i.e. the product of . Now the spelling is made a little more informal and shortened further: We agree as an abbreviation for the assignment described above.
In the second image above, this has been done. The corners became the first three base points in the order "right 100, top 010, left 001" and the height intersection became the unit point , the coordinates of the other points result as follows: The third point on a straight line must result from binary addition without carryovers (also called exclusive-or-combination XOR ) of the other two points on the straight line. For example:, in words: The center of the lower side of the equilateral triangle (101) lies on the lower side (first "sum"), the height to this side (second "sum") and on the inscribed circle (third "sum") ). The fact that these equations work for the “sums” now just means that the vector lies in the respective product of the summed, different coordinate vectors. Since the three side centers, i.e. the points that do not belong to the complete square, can be coordinated consistently with this rule, the "visualization as an equilateral triangle" is formally more precise: the corresponding hypergraph is isomorphic. The definition by enumeration now simply reflects the point set and line set of the hypergraph and is therefore isomorphic to the other two models.
properties
- The Fano plane is a two-dimensional projective space over a finite body in the sense of linear algebra.
- It is therefore also a linear space .
- It is a Pappus two-dimensional projective geometry and therefore a projective plane in the sense of synthetic geometry.
- Every projective plane of order 2 is isomorphic to the Fano plane and there is no projective plane of lower order.
- It is a symmetrical (7,3,1) block plan , making it the smallest Hadamard block plan .
Degenerations
Due to its small size, the Fano level has some special features:
- It fulfills the Pappos theorem “empty”, so to speak: Since there are no nondegenerate hexagons of the kind required by the Pappos configuration, (at least) two of the six corners coincide. But then at least two “intersection points of opposing sides” coincide and the statement of the sentence that these three intersection points lie on a straight line becomes trivial.
- Since a non-degenerate Desargues configuration requires ten different points, Desargues' theorem is ultimately also fulfilled in a trivial way.
- It is the only projective plane above a sloping body in which any projective perspectivity with a center outside of an axis is necessarily the identity. Due to the specifications, the “free” point sets on the straight line through the center are single-point (at least one point of each of these straight lines is on , another is the center). So the transitivity requirement for levels of Lenz-Barlotti class VII.2 is also fulfilled empty. The Fano level belongs to this class VII.2 like any other Desargue's level.
- The double ratio is degenerate because there are no four different points on any straight line .
- The Fano plane is the only projective plane in which the unit point for defining a projective point base is actually superfluous: In the vector space model, every one-dimensional space contains only one further point in addition to the zero vector, that is, the indirect assignment “basis vector → one-dimensional subspace ↔ projective Point ”can also be reversed to the basis vector without using a unit point as an aid; this is exactly the same for projective spaces of any dimension , if, but only if the body has exactly two elements. When choosing the point base in the plane, this peculiarity is shown as follows: If you have chosen three non-collinear points for the point base - there are at least options for this choice, taking into account the sequence - then there is always exactly one point in the plane that is not collinear with two of the selected points!
- In the automorphism group of , the last mentioned peculiarity is expressed in that the statement follows from the isomorphism statement valid for any body , because the multiplicative group is the one group for the two-element body.
Dualization
An abstract dualization of the Fano level is obtained by exchanging the point set and line set in one of the definitions and reversing the incidence relation , i.e. looking at the incidence structure . The incidence structure derived in this way is always again an incidence structure and for a projective level (in the sense of synthetic geometry) also again a projective level of the same order. For Desargue's projective levels and therefore also for the Fano level, the dual structure is isomorphic to the initial structure . This is shown with the help of a concrete isomorphism (a correlation ), which depends on the chosen coordinate system. Such a correlation (here more precisely: a projective, hyperbolic polarity ) is described in the following section:
Line coordinates and duality
In the vector space model, every straight line , i.e. every two-dimensional subspace of the, can be described by a homogeneous straight line equation . The coordinate vector of the straight line (straight line coordinates) is . The straight line with the homogeneous straight line coordinates is assigned to a point with the projective point coordinates and vice versa. The figure on the right shows the assignments for the choice of the point base made in this article: The points at the bottom of the image are assigned to the straight lines directly above them through this correlation, the straight lines to the point directly below them. For example, the 3rd base point 001, the lower right corner of the triangle, is assigned to the straight line with the equation (the left side of the triangle) , the height through the upper tip with the equation is assigned to its height base point 101.
In the picture on the right, the lines in the middle between the lines and points highlighted in red represent the incidence relation, which is reversed by the dualization: or , in terms of set theory , in the vector space model , where the smaller symbol stands for "is linear subspace of".
Collineation group
The automorphism group of the Fano plane is the group of its collineations ; it agrees with the group of its projectivities , since the two-element prime body does not allow any non- identical body automorphisms. It operates sharply transitive on the ordered non-collinear point triples and therefore has the order ; the same order results from the formula for the order of the general linear group . It is non-Abelian and simple (i.e. it has only the trivial normal divisors ).
In the following, group-theoretical considerations, a group of permutations of their points, i.e. a subgroup of the symmetrical group, is presented. It is agreed that permutations operate on numbers from the left , that is, it applies and z. B. . In the language of geometry, two projectivities are conjugated to one another if and only if they have the same representation with regard to a suitable point base as with regard to our starting basis (as a linear mapping). In the permutation representation this means that the level can be renumbered according to the “binary” system described above so that the permutation representation assumes from. Two permutations are conjugated in the if and only if they have similar representations as products of disjoint cycles, so this condition is also necessary in , it also proves to be sufficient there - except for the elements of order 7, which split into two conjugation classes .
2 groups and perspectives
- For each of the 7 straight lines there is a group of plane perspectives with an axis. If a perspective has another fixed point outside the axis, then it is the identity, since every straight line has only three points. Therefore, all non-identical perspectives have their center on the axis and swap the two points that lie apart from the two straight lines through which are different from the axis :
- The group of perspectives with axis and center is a
3 groups and the affinity group
- If the points are on a straight line, then two of the perspective groups together create a subgroup of 24 elements. For example, as the product of perspectives, the product of these three generators is the element , an element of order 3. This element is already conjugated in to its inverse , therefore it contains a subgroup that is isomorphic to the dihedral group. As a subgroup with 24 elements, three of the 2-Sylow groups contains the collineation group with 8 elements: for
- The group is isomorphic to the symmetrical group because it maps the straight line onto itself as a fixed line and therefore operates faithfully on the longitudinally slotted plane as a group of affinities. The full affinity group of the affine plane with 4 points is just that .
- All 56 elements of order 3 are conjugate to each other and to , so they always have the form of a product of two disjoint 3-cycles, one cycle containing collinear points, the other 3 of the four non-collinear points outside of those determined by the first cycle Straight lines.
- Each of the 28 3-Sylow groups of group order 3 is generated by one of the mentioned elements of order 3.
7-groups and small generating systems
- In there are exactly 48 projectivities of order 7, which are each represented as a 7 cycle.
- Each of these group elements creates a 7-Sylow group of isomorphic type that contains a total of 6 7-cycles. Two different of these 7 Sylow groups intersect in the trivial group, so there are exactly 8 subgroups of this type.
- The set of 7-cycles is divided into two conjugation classes with 24 elements each.
- Each 7-cycle is completely determined by any four points , which it maps onto one another in this order , whereby they are not collinear and always
- either on the connecting line (first conjugation class)
- or lies on the connecting line (second conjugation class).
- If an element of order 7 (7-cycle), then is conjugated to if and only if a quadratic remainder is modulo 7, that is, are in the same conjugation class as and in the other.
- The cyclic collineation generated by a 7-cycle is a Singer-cycle , therefore, exists for each cycle 7 a bijection ( "renumbering") of the set of points, after which the renumbered Fano plane of the difference set is derived .
- If two projectivities are of order 7, then by Sylow's theorems and da is simple: or . That is, the automorphism group is generated by two suitably chosen 7-cycles, for example: with
- Each 7-cycle can be represented as a composition from exactly three different, non-identical perspectives. For the two cycles from the previous statement is or with the perspectives .
- From this it follows: as a product of three perspectives and as a product of a perspectivity and a projectivity of order 4.
See also
The multiplication of the octonions can be represented in the Fano plane.
literature
General
- Peter Dembowski : Finite geometries . Reprint of the 1968 edition. Springer, Berlin / Heidelberg / Singapore / Tokyo / New York / Barcelona / Budapest / Hong Kong / London / Milan / Paris / Santa Clara 1997, ISBN 3-540-61786-8 .
- Jacobus Hendricus van Lint , Richard M. Wilson : A Course in Combinatorics . Reprint of the 2nd edition. Cambridge Univ. Press, Cambridge et al. a. 2004, ISBN 0-521-00601-5 , pp. 225, 237–239 ( excerpt from Google book search).
- T. Pisanski, M. Randić: Bridges between Geometry and Graph Theory . In: CA Gorini (ed.): Geometry at Work . A Collection of Papers Showing Applications of Geometry. Math. Assoc. Amer., Washington, DC 2000, pp. 174-194 .
Applications of the Fano level to math puzzles
- David Wells: The Penguin Dictionary of Curious and Interesting Geometry . 1st edition. Penguin, London 1986, ISBN 0-14-008029-5 (English, Recreational mathematics, elementary number theory).
To the group theoretical statements
- Thomas W. Hungerford: Algebra . corrected 5th edition. Springer, Berlin / Heidelberg / New York 2003, ISBN 0-387-90518-9 , Chapter I Groups, 5-7.
- Bartel Leendert van der Waerden : Algebra . Using lectures by E. Artin and E. Noether. 9th edition. tape 1 . Springer, Berlin / Heidelberg / New York 1993, ISBN 3-540-56799-2 .
Web links
- Eric W. Weisstein : Fano Plane . In: MathWorld (English).
- Finite Level and Fano Level at PlanetMath (English)
- The group of Walsh permutations (see v: en: 3-bit Walsh permutation ) on an 8-element set is isomorphic to the automorphism group of the Fano level.
References and comments
- ↑ Dembowski (1968), Chapter 1
- ↑ According to the definition, the incidence relation is symmetrical as in every projective plane, therefore and
- ↑ For the 7-cycle c, choose that of the powers that is in the first conjugation class, then there is such a bijection through which becomes.
- ↑ Note that all perspectives are and therefore is involutive .