Set of pappos
The Pappos Theorem (Pappus) , sometimes also called Pappos-Pascal's Theorem, is a central theorem in affine and projective geometry . It appeared for the first time as Proposition 139 in Book VII of the Mathematical Collections of the ancient Greek mathematician Pappos of Alexandria . Blaise Pascal found a generalization of the theorem in the 17th century, the Pascal theorem named after him , in which the six basic points of the theorem lie on a conic section .
In its more general projective form, the sentence reads :
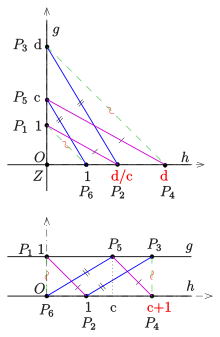
If six points of a projective plane lie alternately on two straight lines and , then the points are
collinear, d. i.e., they lie on a straight line (see picture).
If the two straight lines and through the hexagonal points and the straight line are copunctal , one also speaks of Pappos' little theorem .
Since two straight lines do not necessarily intersect in an affine plane , the sentence is also formulated in a more special affine form :
If six points of an affine plane lie alternately on two straight lines and and are both
- Pair of lines as well as that
- Pair of straight lines parallel,
so are and parallel (see picture).
In the projective closure of the underlying affine plane, the three parallel pairs of straight lines intersect on the improper straight line , and the projective form of Pappos' theorem arises.
Proof of the theorem in an affine plane over a body
Because of the parallelism in an affine plane, one has to differentiate between two cases, depending on whether the straight lines intersect or not. The key to a simple proof is the always possible suitable coordination of the affine plane. Because in a 2-dimensional vector space one can freely choose the zero point and two ( linearly independent ) basis vectors.
Case 1: The two straight lines intersect and let it be .
In this case, coordinates can be introduced so that is (see picture). The points then have coordinates . Since the straight lines are parallel, the following applies . From the parallelism of the straight lines it follows that it must be. So the straight line has the slope and is therefore parallel to .
Case 2: .
In this case the coordinates are chosen so that is. From the parallelism and follows and and thus the parallelism .
Dual set of pappos
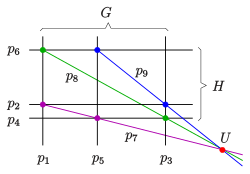
Due to the duality principle for projective levels, the dual theorem of Pappos also applies :
If six straight lines belong to a projective plane, alternating two straight line bundles through two points , then the straight lines are
copunctival, d. i.e., they go through a common point . The left image shows the projective version, the right image an affine version in which the points lie on the distant line.
If in the affine version of Pappos 'dual theorem point is also a far point, then the dual statement of Pappos' small theorem arises , which is identical to Thomsen's theorem from elementary triangular geometry. The Thomsen figure plays an essential role in coordinating an axiomatically defined projective plane. The proof for the inference of the Thomsen figure follows from the proof of Pappus' little theorem above. But the direct proof is also very simple:
Since the formulation of Thomsen's inference theorem only uses the terms connect, intersect and parallel , the theorem is affine invariant and one can assume for proof that it holds (see picture). The starting point for the line is the point . One easily calculates the coordinates of the remaining points and recognizes that the 7th point is again the starting point.
Meaning: Pappos planes
Pappos' theorem does not apply in every projective plane. It only applies in those levels that can be coordinated with the help of a (commutative) body . Conversely, the validity of Pappos' theorem means that the plane can be coordinated with a coordinate body. Such planes, affine or projective, are characterized by Pappos' theorem and are called Pappos planes .
For an overview of affine and projective planes, in which the Pappos theorem or weaker closure theorems apply in general, and the conclusions that result for the algebraic structure of the coordinate domain, see the articles “ Ternary bodies ” and “ Classification of projective planes ”.
Pappos' projective theorem as an axiom and equivalent statements
As already explained in the section Meaning , Pappos' projective theorem is independent of the incidence axioms of a projective plane , therefore it or statements equivalent to it (based on the incidence axioms) are also referred to as an axiom , here abbreviated as (PA). This axiom is also independent of the Fano axiom , here for short (FA), because they exist
- projective planes over each commutative field with one of 2 different characteristics . You meet (FA) and (PA),
- projective planes over every commutative field with characteristic 2. They never fulfill (FA), but always (PA),
- projective planes that are not Papposian and also do not fulfill (FA), since there are non-commutative skew bodies with the characteristic for every prime number , i.e. also those with the characteristic 2,
- projective planes that are not Papposian, but fulfill (FA), since there is at least one non-commutative skew body for every odd prime number characteristic and for characteristic 0.
→ Compare also Gleason's theorem and Hanna Neumann's theorem in Fano's axiom # AntiFano .
The following synthetic and analytical statements about a projective level are equivalent:
- is pappossch.
- is desargue and the coordinate skewed body of is commutative.
- One of or the equivalent of each of the coordinates of the ternary field of is isomorphic to a commutative field.
- There is a line in such that the affine plane satisfies Pappos' affine theorem.
- The previous statement applies to every straight line in the plane.
Relation to Desargues theorem: Hessenberg's theorem
As Hessenberg's theorem , in projective geometry, the statement
- On a projective level in which Pappos' theorem is generally valid, Desargues's theorem is also generally valid .
designated. This sentence was proved (incompletely) by Gerhard Hessenberg , after whom it is named, in 1905. It is of fundamental importance for synthetic geometry . A complete proof (via various auxiliary sentences) can be found in the Lüneburg textbook.
That means: From the axiom of Pappos (PA) follows the axiom of Desargues. That the reversal in general (more precisely, for un finite projective planes) is wrong is proved by the existence of projective planes over non-commutative skew fields.
Conclusion for finite planes from the Hessenberg theorem
With Wedderburn's theorem it follows that for finite projective or affine planes the Pappos theorem and the Desargues theorem are equivalent .
literature
On the history of the Pappos theorem
- Harold Scott MacDonald Coxeter with SL Greitzer: Timeless geometry . Klett, Stuttgart 1983, ISBN 3-12-983390-0 .
- Carl Immanuel Gerhardt : The collection of the Pappus of Alexandria, Greek and German in 2 volumes . HW Schmidt, Halle / Eisleben (1871, 1875).
- Thomas Heath: A History of Greek Mathematics . Dover, New York 1981 (first edition: 1921).
Textbooks
- Harold Scott MacDonald Coxeter: Introduction to Geometry . 2nd Edition. John Wiley & Sons, New York 1969, ISBN 978-0-471-50458-0 .
- Helmut Karzel, Kay Sörensen, Dirk Windelberg: Introduction to Geometry . Vandenhoeck & Ruprecht, Göttingen 1973, ISBN 3-525-03406-7 .
- Lars Kadison, Matthias T. Kromann: Projective Geometry and Modern Algebra . Birkhäuser, Boston / Basel / Berlin 1996, ISBN 3-7643-3900-4 ( table of contents (PDF) [accessed on August 6, 2013] Formulates and proves simple transitivity properties of the projective group that are equivalent to Pappos' theorem; dependencies between the 3 axioms: Fano, Desargues and Pappos).
- Heinz Lüneburg : The Euclidean plane and its relatives . Birkhäuser, Basel / Boston / Berlin 1999, ISBN 3-7643-5685-5 , III: Papossche Ebene ( reading excerpt books.google.de [accessed on July 30, 2013]) Detailed discussion and proof of the Hessenberg theorem, explanations, such as the Pappos' theorem determines the algebraic structure of the coordinate field).
- Hanfried Lenz : Lectures on projective geometry . Akad. Verlag, Leipzig 1965.
- Rolf Lingenberg : Fundamentals of Geometry I . Bibliographical Institute, Mannheim 1969.
Web links
- Projective geometry , short script, University of Darmstadt (PDF; 180 kB)
- Siegfried Krauter: Introduction to Finite Geometry . (PDF) PH Ludwigsburg, script
- Pappus's Theorem: Nine proofs and three variations
References and comments
- ↑ Strictly speaking, it should be called an “axiom” today, since it is always valid in real geometry, but in the geometries now called “affine” or “projective” only if the geometry under consideration is coordinated by a body can. Heinz Lüneburg : The Euclidean plane and its relatives . Birkhäuser, Basel / Boston / Berlin 1999, ISBN 3-7643-5685-5 , III: Papos planes.
- ^ Carl Immanuel Gerhardt : The Collection of the Pappus of Alexandria, Greek and German in 2 volumes . HW Schmidt, Halle / Eisleben (1871, 1875).
- ^ W. Blaschke: Projektive Geometrie , Springer-Verlag, 2013, ISBN 3034869320 , p. 190
- ^ Heinz Lüneburg : The Euclidean plane and its relatives . Birkhäuser, Basel / Boston / Berlin 1999, ISBN 3-7643-5685-5 , III: Papos planes. Definition 1.1, the notation Pappus level is often found .
- ^ A b Kadison and Kromann (1996): 7.3: A Noncommutative Division Ring with Characteristic p .
- ^ A b c Heinz Lüneburg : The Euclidean plane and its relatives . Birkhäuser, Basel / Boston / Berlin 1999, ISBN 3-7643-5685-5 , III.1. - Hessenberg's theorem .
- ↑ a b c Hanfried Lenz : Lectures on projective geometry . Akad. Verlag, Leipzig 1965.
- ^ Lars Kadison, Matthias T. Kromann: Projective Geometry and Modern Algebra . Birkhäuser, Boston / Basel / Berlin 1996, ISBN 3-7643-3900-4 . 6.3. Pappus' theorem