Lie-type group

Groups of the Lie type are groups investigated in the mathematical subfield of group theory , which are derived from certain Lie algebras , more precisely they are groups of automorphisms of Lie algebras. With the finite among these is obtained 16 infinite series finite simple groups , together with the cyclic groups of prime - order and the alternating groups , the 18 series from the classification set of finite simple groups form.

Table overview

We start with a tabular overview, which is adapted from the textbook "Finite group Theory" by Michael Aschbacher .

Surname	Alternative name	Group order	Exceptions	Isomorphies
${\displaystyle A_{n}(q)}$	Special projective linear group	${\displaystyle {\frac {q^{n(n+1)/2}}{(n+1,q-1)}}\prod _{i=1}^{n}(q^{i+1}-1)}$	${\displaystyle A_{1}(2),A_{1}(3)}$	${\displaystyle A_{1}(4)\cong A_{1}(5)\cong A_{5}}$ ${\displaystyle A_{1}(7)\cong A_{2}(2)}$ ${\displaystyle A_{1}(9)\cong A_{6}}$ ${\displaystyle A_{3}(2)\cong A_{8}}$
${\displaystyle B_{n}(q),n>1}$	Commutator group of the special orthogonal group (odd degree)	${\displaystyle {\frac {q^{n^{2}}}{(2,q-1)}}\prod _{i=1}^{n}(q^{2i}-1)}$		${\displaystyle B_{n}(2^{m})\cong C_{n}(2^{m})}$ ${\displaystyle B_{2}(3)\cong {}^{2}\!A_{3}(2^{2})}$
${\displaystyle C_{n}(q),n>2}$	Projective symplectic group	${\displaystyle {\frac {q^{n^{2}}}{(2,q-1)}}\prod _{i=1}^{n}(q^{2i}-1)}$		${\displaystyle B_{n}(2^{m})\cong C_{n}(2^{m})}$
${\displaystyle D_{n}(q),n>1}$	Commutator group of the special orthogonal group (even degree)	${\displaystyle {\frac {q^{n(n-1)}(q^{n}-1)}{(4,q^{n}-1)}}\prod _{i=1}^{n}(q^{2i}-1)}$
${\displaystyle E_{6}(q)}$	Chevalley group	${\displaystyle {\frac {q^{36}}{(3,q-1)}}\prod _{i=2,5,6,8,9,12}(q^{i}-1)}$
${\displaystyle E_{7}(q)}$	Chevalley group	${\displaystyle {\frac {q^{63}}{(2,q-1)}}\prod _{i=2,6,8,10,12,14,18}(q^{i}-1)}$
${\displaystyle E_{8}(q)}$	Chevalley group	${\displaystyle q^{120}\prod _{i=2,8,12,14,18,20,24,30}(q^{i}-1)}$
${\displaystyle F_{4}(q)}$	Chevalley group	${\displaystyle q^{24}\prod _{i=2,6,8,12}(q^{i}-1)}$
${\displaystyle G_{2}(q)}$	Chevalley group	${\displaystyle q^{6}(q^{6}-1)(q^{2}-1)}$	${\displaystyle G_{2}(2)}$
${\displaystyle {}^{2}\!A_{n}(q^{2}),n>1}$	Special unitary group	${\displaystyle {\frac {q^{n(n+1)/2}}{(n+1,q+1)}}\prod _{i=1}^{n}(q^{i+1}-(-1)^{i+1})}$	${\displaystyle {}^{2}\!A_{2}(2^{2})}$	${\displaystyle {}^{2}\!A_{3}(2^{2})\cong B_{2}(3)}$
${\displaystyle {}^{2}\!B_{2}(2^{2m+1})}$	Suzuki groups ${\displaystyle \mathrm {Sz} (2^{2m+1})}$	${\displaystyle q^{2}(q^{2}-1)(q-1)}$ With ${\displaystyle q=2^{2m+1}}$	${\displaystyle {}^{2}\!B_{2}(2)}$
${\displaystyle {}^{2}\!D_{n}(q^{2}),n>3}$	Steinberg Group	${\displaystyle {\frac {q^{n(n-1)}(q^{n}+1)}{(4,q^{n}+1)}}\prod _{i=1}^{n-1}(q^{2i}-1)}$
${\displaystyle {}^{3}\!D_{4}(q^{3})}$	Steinberg Group	${\displaystyle q^{12}(q^{8}+q^{4}+1)(q^{6}-1)(q^{2}-1)}$
${\displaystyle {}^{2}\!E_{6}(q^{2})}$	Steinberg Group	${\displaystyle {\frac {q^{36}(q^{n}+1)}{(3,q+1)}}\prod _{i=2,5,6,8,9,12}(q^{i}-(-1)^{i}}$
${\displaystyle {}^{2}\!F_{4}(2^{2m+1})}$	Ree group	${\displaystyle q^{12}(q^{6}+1)(q^{4}-1)(q^{3}+1)(q-1)}$ With ${\displaystyle q=2^{2m+1}}$	${\displaystyle {}^{2}\!F_{4}(2)}$
${\displaystyle {}^{2}\!G_{2}(3^{2m+1})}$	Ree group	${\displaystyle q^{3}(q^{3}+1)(q-1)}$ With ${\displaystyle q=3^{2m+1}}$	${\displaystyle {}^{2}\!G_{2}(3)}$

The names result from the types of Lie algebras, as explained below. In the above table there is always a prime power and a natural number including 0, the brackets in the denominators of the formulas for the group order stand for the greatest common factor . Many of these groups were known as so-called classical groups even before Chevalley's work, and some are also named after their discoverers. The names resulting from this are given as "alternative names". The exceptions mentioned are non-simple groups, and the isomorphies mentioned in the "Isomorphism" column exist among these groups and with the alternating groups A _n ( if the Lie type is meant, a prime power in brackets always follows). ${\displaystyle q}$ ${\displaystyle m}$ ${\displaystyle (\cdot ,\cdot )}$ ${\displaystyle A_{n}}$

In the following, the terms needed to define these groups are developed, essentially following the textbook "Simple Groups of Lie-Type" by Roger Carter given below , which is entirely devoted to this topic, even if this book is older and from the Time before the classification set originates. Starting from the simple classification Lie algebra over , we describe the quite complicated structure of these groups and run it just enough terms that such is necessary to define the groups. ${\displaystyle \mathbb {C} }$

The representation is divided into two large blocks. First we construct the so-called classical Chevalley groups, the theory of which goes back to Claude Chevalley ; these are the groups without an upper left index in their name. In the second block automorphisms are constructed on certain classical Chevalley groups whose order is precisely the left upper index. The so-called twisted Chevalley groups are constructed as subgroups of the classical Chevalley groups from certain fixed point sets of these automorphisms . These were discovered independently by Robert Steinberg , Jacques Tits and Ravi Hertzig .

Simple Lie algebras

Root systems

Let it be a simple, finite-dimensional Lie algebra over and the non-degenerate killing form . Then, according to the theory of Lie algebras, there is a so-called Cartan decomposition ${\displaystyle (L,[\cdot ,\cdot ])}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle (\cdot ,\cdot )_{L}}$

${\displaystyle L=H\oplus \bigoplus _{r\in \Phi }L_{r}}$, in which

• ${\displaystyle H}$a Cartan subalgebra , it is even true , ${\displaystyle [H,H]=0}$
• ${\displaystyle \Phi \subset H}$a so-called root system in the - linear envelope of , ${\displaystyle \mathbb {R} }$ ${\displaystyle H_{\mathbb {R} }}$ ${\displaystyle \Phi }$
• ${\displaystyle L_{r}=\mathbb {C} e_{r}\subset L}$for each a one-dimensional subspace , a vector is out ${\displaystyle r\in \Phi }$ ${\displaystyle e_{r}}$ ${\displaystyle L_{r}\setminus \{0\}}$
• ${\displaystyle [H,L_{r}]=L_{r}}$for all , ${\displaystyle r\in \Phi }$
• ${\displaystyle [h,e_{r}]=(h,r)_{L}\cdot e_{r}}$for everyone . ${\displaystyle r\in \Phi ,h\in H}$

${\displaystyle H_{\mathbb {R} }}$is a Euclidean space with the restriction of the killing form , in which one can therefore measure lengths and angles between vectors, and the properties of the root system lead to severe restrictions on the relative lengths of the vectors and the angles between them. As with any root system, one can select a subset of so-called fundamental roots so that ${\displaystyle \Phi }$ ${\displaystyle \Phi _{0}\subset \Phi }$

• ${\displaystyle \Phi _{0}=\{r_{1},\ldots ,r_{n}\}}$a vector space basis of is ${\displaystyle H_{R}}$
• all coefficients in the expansion of a vector after the base have the same sign ${\displaystyle r\in \Phi }$ ${\displaystyle \Phi _{0}}$
• ${\displaystyle n_{i,j}:={\frac {4(r_{i},r_{j})_{L}^{2}}{(r_{i},r_{i})_{L}(r_{j},r_{j})_{L}}}\in \{0,1,2,3\}}$for everyone . ${\displaystyle i\not =j}$

Dynkin diagrams

The Dynkin diagrams are graphs assigned to the root systems.

The so-called Dynkin diagram is constructed from the root system just presented , which is the graph with the set of nodes and edges between . The properties of a root system are so restrictive that there are only the following options, so-called types , shown in the adjacent overview : ${\displaystyle \Phi _{0}}$ ${\displaystyle n_{i,j}}$ ${\displaystyle r_{i},r_{j}\in \Phi _{0}}$

${\displaystyle A_{n},n\geq 1,\quad B_{n},n\geq 2,\quad C_{n},n\geq 3,\quad D_{n},n\geq 4,\quad E_{6},E_{7},E_{8},\quad F_{4},\quad G_{2}}$.

A "<" or ">" stands above the edges between two fundamental roots for a corresponding size relation of the lengths of the fundamental roots.

Despite the many choices in the roughly outlined construction, this represents a complete classification of all simple, finite-dimensional -Lie algebras. Two simple, finite-dimensional -Lie algebras are isomorphic if and only if they have the same Dynkin diagram and to each of the listed ones Dynkin diagrams there is a simple, finite-dimensional Lie algebra. This classification goes back essentially to Élie Cartan and Wilhelm Killing . A simple, finite-dimensional Lie algebra is often referred to simply by its type. ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

Chevalley groups

Chevalley base

We assume a simple, finite-dimensional -Lie algebra and use the terms introduced above. For two roots let ${\displaystyle \mathbb {C} }$ ${\displaystyle L}$ ${\displaystyle r,s\in \Phi }$

• ${\displaystyle h_{r}:={\frac {2r}{(r,r)_{L}}}}$, thereby the fundamental roots are appropriately "normalized".
• ${\displaystyle A_{r,s}:={\frac {2(r,s)_{L}}{(r,r)_{L}}}}$, these numbers are always off . ${\displaystyle \mathbb {Z} }$
• ${\displaystyle p_{r,s}:=\max\{p\in \mathbb {N} _{0}\mid s-pr\in \Phi \}}$.

The course also form a basis of the Cartan algebra , which is why a base of is. ${\displaystyle h_{r_{i}}}$ ${\displaystyle H}$ ${\displaystyle \{h_{r}\mid r\in \Phi _{0}\}\cup \{e_{r}\mid r\in \Phi \}}$ ${\displaystyle L}$

Claude Chevalley has shown that the elections can be made in such a way that what is now known as a Chevalley base is present, which means that the following applies:

• ${\displaystyle [h_{r},h_{s}]=0}$ for all ${\displaystyle r,s\in \Phi }$
• ${\displaystyle [h_{r},e_{s}]=A_{r,s}e_{s}}$ for all ${\displaystyle r,s\in \Phi }$
• ${\displaystyle [e_{r},e_{s}]=0}$for everyone with ${\displaystyle r,s\in \Phi }$ ${\displaystyle r+s\notin \Phi }$
• ${\displaystyle [e_{r},e_{s}]=N_{r,s}e_{r+s}}$for everyone with , being . ${\displaystyle r,s\in \Phi }$ ${\displaystyle r+s\in \Phi }$ ${\displaystyle N_{r,s}=\pm (p_{r,s}+1)}$

Certain options remain with the signs of the . ${\displaystyle N_{r,s}}$

Chevalley groups over ℂ

The above-mentioned relations between the elements of a Chevalley base show that for each the derivation ${\displaystyle r\in \Phi }$

${\displaystyle \mathrm {ad} \,e_{r}:\,L\rightarrow L,\,x\mapsto [e_{r},x]}$

is a nilpotent element of the algebra of linear operators on , that is, for a sufficiently large . This then also applies to every scalar multiple , that is to say to every is ${\displaystyle L}$ ${\displaystyle (\mathrm {ad} \,e_{r})^{m}=0}$ ${\displaystyle m\in \mathbb {N} }$ ${\displaystyle \zeta \cdot \mathrm {ad} \,e_{r}}$ ${\displaystyle \zeta \in \mathbb {C} }$

${\displaystyle x_{r}(\zeta ):=\exp(\zeta \cdot \mathrm {ad} \,e_{r})=\mathrm {id} _{L}+\sum _{k\geq 1}{\frac {1}{k!}}\zeta ^{k}(\mathrm {ad} \,e_{r})^{k}}$

a finite sum. Hence the usual proof that the exponential function of a derivation is an automorphism works. The group generated by the automorphisms is called the Chevalley group and is denoted by. The Lie algebra can also be replaced by its type, i.e. one writes . The operation of on the elements of a Chevalley basis can also be obtained from the relations mentioned above: ${\displaystyle x_{r}(\zeta ),\,r\in \Phi ,\zeta \in \mathbb {C} }$ ${\displaystyle L(\mathbb {C} )}$ ${\displaystyle L}$ ${\displaystyle A_{n}(\mathbb {C} ),B_{n}(\mathbb {C} ),\ldots }$ ${\displaystyle x_{r}(\zeta )}$

• ${\displaystyle x_{r}(\zeta )h_{r}=h_{r}-2\zeta e_{r}}$
• ${\displaystyle x_{r}(\zeta )e_{r}=e_{r}}$
• ${\displaystyle x_{r}(\zeta )e_{-r}=e_{-r}+\zeta h_{r}-\zeta ^{2}e_{r}}$
• ${\displaystyle x_{r}(\zeta )h_{s}=h_{s}-A_{s,r}\zeta e_{r}}$   for linearly independent of r ${\displaystyle s\in \Phi }$
• ${\displaystyle x_{r}(\zeta )e_{s}=\sum _{i=0}^{k}M_{r,s,i}\zeta ^{i}e_{ir+s}}$,

wherein is determined by the fact that all to include for and ${\displaystyle k}$ ${\displaystyle ir+s}$ ${\displaystyle \Phi }$ ${\displaystyle 0\leq i\leq k}$

${\displaystyle M_{r,s,i}:={\frac {1}{i!}}\prod _{j=0}^{i-1}N_{r,jr+s}=\pm {\frac {(p_{r,s}+1)\cdots (p_{r,s}+i)}{i!}}=\pm {\binom {p+i}{i}}\in \mathbb {Z} }$

Chevalley groups over K

Another simple conclusion from the above relations between the elements of a Chevalley basis is that the -linear hull is closed with respect to the Lie bracket and therefore forms a Lie ring , i.e. it satisfies all axioms of a Lie algebra except for those which concern the scalar multiplication . If there is an arbitrary field, the tensor product can be formed, because every field is naturally a Modul-module . Every element of has the shape ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Z} \Phi }$ ${\displaystyle \mathbb {Z} \Phi }$ ${\displaystyle K}$ ${\displaystyle K\otimes _{\mathbb {Z} }\mathbb {Z} \Phi }$ ${\displaystyle K\otimes _{\mathbb {Z} }\mathbb {Z} \Phi }$

${\displaystyle \sum _{r\in \Phi _{0}}t_{r}(1_{K}\otimes h_{r})+\sum _{r\in \Phi }s_{r}(1_{K}\otimes e_{r})}$,

where the one element is in and the elements are off. By laying down ${\displaystyle 1_{K}}$ ${\displaystyle K}$ ${\displaystyle t_{r},s_{r}}$ ${\displaystyle K}$

${\displaystyle [1_{K}\otimes x,1_{K}\otimes y]:=1_{K}\otimes [x,y]}$

we get a -Lie algebra . The set is a basis of and, according to the definition of the Lie bracket, the same relations apply as between the elements of the Chevalley basis, whereby every integer that occurs in the relations is to be understood as, i.e. every integer becomes like usually mapped to an element of the prime field of , this is no longer mentioned in the following. ${\displaystyle K}$ ${\displaystyle L_{K}}$ ${\displaystyle \{1_{K}\otimes h_{r}\mid r\in \Phi _{0}\}\cup \{1_{K}\otimes e_{r}\mid r\in \Phi \}}$ ${\displaystyle L_{K}}$ ${\displaystyle L_{K}}$ ${\displaystyle a}$ ${\displaystyle a\cdot 1_{K}\in K}$ ${\displaystyle K}$

Analogously, it is now as follows operators to explain. With regard to the Chevalley basis, each has a matrix representation with matrix elements , as can be seen from the above formulas for the operation of the on the basis elements. For each , the matrix with the corresponding matrix elements then defines an automorphism denoted by . This operates as follows on the basic elements: ${\displaystyle x_{r}(t)}$ ${\displaystyle L_{K}}$ ${\displaystyle x_{r}(\zeta )}$ ${\displaystyle a\zeta ^{i},\,a\in \mathbb {Z} ,i\in \mathbb {N} _{0}}$ ${\displaystyle x_{r}(\zeta )}$ ${\displaystyle t\in K}$ ${\displaystyle at^{i}}$ ${\displaystyle x_{r}(t)}$ ${\displaystyle L_{K}}$

• ${\displaystyle x_{r}(t)h_{r}=h_{r}-2te_{r}}$
• ${\displaystyle x_{r}(t)e_{r}=e_{r}}$
• ${\displaystyle x_{r}(t)e_{-r}=e_{-r}+th_{r}-t^{2}e_{r}}$
• ${\displaystyle x_{r}(t)h_{s}=h_{s}-A_{s,r}te_{r}}$   for linearly independent of r ${\displaystyle s\in \Phi }$
• ${\displaystyle x_{r}(t)e_{s}=\sum _{i=0}^{k}M_{r,s,i}t^{i}e_{ir+s}}$   with the same as in the above formulas for ${\displaystyle k}$ ${\displaystyle x_{r}(\zeta )}$

Note that all the coefficients in these equations are integers.

The group generated by the automorphisms is called the Chevalley group above and is denoted by. ${\displaystyle x_{r}(t),\,r\in \Phi ,t\in K}$ ${\displaystyle K}$ ${\displaystyle L(K)}$

${\displaystyle L(K):=\langle x_{r}(t)\mid r\in \Phi ,t\in K\rangle }$

With the exception of isomorphism, the groups are clearly determined by the isomorphism classes of the simple, finite-dimensional Lie algebra and the field . Is finite is already uniquely determined by the number of its elements, which must be a prime power , except for isomorphism, and one therefore writes instead . Instead of specifying the type, it is sufficient, and one therefore writes . The following sentence applies to these groups: ${\displaystyle L(K)}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle L}$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle q}$ ${\displaystyle L(q)}$ ${\displaystyle L(K)}$ ${\displaystyle L}$ ${\displaystyle A_{n}(q),B_{n}(q),\ldots }$

If -Lie is a simple, finite-dimensional algebra and a field, then the Chevalley group is simple with a few exceptions . ${\displaystyle L}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle K}$ ${\displaystyle L(K)}$ ${\displaystyle A_{1}(2),A_{1}(3),B_{2}(2),G_{2}(2)}$

This explains the first nine series of simple groups in the table above.

Twisted Chevalley groups

Automorphisms on Dynkin diagrams

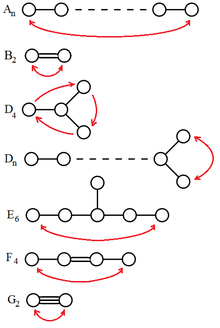
Non-trivial automorphisms on Dynkin diagrams.

The twisted Chevalley groups are subgroups of the Chevalley groups, which are formed from certain fixed point sets of a suitable automorphism of the Chevalley group. Such an automorphism arises from a graph automorphism of the Dynkin diagram. Therefore we first get an overview of the possible graph automorphisms. On the Dynkin diagrams one has for the non-trivial automorphism, which mirrors the graph at the horizontal center, as indicated in the adjacent drawing. ${\displaystyle \sigma }$ ${\displaystyle A_{n}}$ ${\displaystyle n\geq 2}$

There are no non-trivial graph automorphisms on the Dynkin diagrams with , because every graph automorphism must define the single node with only one edge and the distances to this node. For of course is not true and here there is a non-trivial automorphism as shown in the adjacent drawing. The same applies to , is not listed as this coincides with . ${\displaystyle B_{n}}$ ${\displaystyle n>2}$ ${\displaystyle B_{2}}$ ${\displaystyle C_{n}}$ ${\displaystyle C_{2}}$ ${\displaystyle B_{2}}$

On one has the exchange of the two right ends as graph automorphism. A peculiarity arises with , here the given rotation is also a non-trivial graph automorphism. ${\displaystyle D_{n}}$ ${\displaystyle D_{4}}$

In the -diagrams there is exactly one node with three edges, which must therefore remain fixed under each graph automorphism. The above at shows given distance argument that and can not have non-trivial Graphenautomorphismen, has indicated in the drawing Graphenautomorphismus. For and the graph automorphism is obvious. ${\displaystyle E_{n}}$ ${\displaystyle B_{n}}$ ${\displaystyle E_{7}}$ ${\displaystyle E_{8}}$ ${\displaystyle E_{6}}$ ${\displaystyle F_{4}}$ ${\displaystyle G_{2}}$

Note that almost all of the given graph automorphisms have order 2. The only exception is the Dynkin diagram , on which there is a graph automorphism of order 2 and one of order 3. ${\displaystyle D_{4}}$

Automorphisms on the Chevalley groups

If there is a graph automorphism on a Dynkin diagram, one can actually find an automorphism of the associated Chevalley group, which maps for each to , where the field in the case of and perfect and of the characteristic 2 and in the case of perfect and of the Characteristic 3 must be. ${\displaystyle \rho }$ ${\displaystyle \sigma }$ ${\displaystyle X_{r}:=\{x_{r}(t)|t\in K\}}$ ${\displaystyle r\in \Phi _{0}}$ ${\displaystyle X_{\rho (r)}}$ ${\displaystyle K}$ ${\displaystyle B_{2}}$ ${\displaystyle F_{4}}$ ${\displaystyle G_{2}}$

In order for the group automorphism to have the same order as the graph automorphism , certain field automorphisms have to be brought into play, which in the case of the finite fields we are interested in leads to further restrictions, which are represented as follows, where always stands for a prime power: ${\displaystyle \sigma }$ ${\displaystyle \rho }$ ${\displaystyle q}$

• Type : must be a square, so ${\displaystyle A_{n},D_{n},E_{6}}$ ${\displaystyle |K|}$ ${\displaystyle |K|=q^{2}}$
• Type (with ): must be a third power, so ${\displaystyle D_{4}}$ ${\displaystyle \mathrm {ord} (\rho )=3}$ ${\displaystyle |K|}$ ${\displaystyle |K|=q^{3}}$
• Type :   with ${\displaystyle B_{2},F_{4}}$ ${\displaystyle |K|=2^{2m+1}}$ ${\displaystyle m\in \mathbb {N} _{0}}$
• Type :   with ${\displaystyle G_{2}}$ ${\displaystyle |K|=3^{2m+1}}$ ${\displaystyle m\in \mathbb {N} _{0}}$

Construction of the twisted Chevalley groups

For finite fields with elements, a prime power, there is a corresponding group automorphism of the same order on the associated Chevalley group, which maps every set to the non-trivial graph automorphism of the Dynkin diagram , under the restrictions mentioned above . With this group automorphism , a subgroup is now formed as follows, whereby it should be noted that the overall construction is still based on a simple, finite-dimensional -Lie algebra and therefore all the terms introduced above are available. One defines ${\displaystyle K}$ ${\displaystyle q^{i}}$ ${\displaystyle q}$ ${\displaystyle \rho }$ ${\displaystyle \sigma }$ ${\displaystyle X_{r},r\in \Phi _{0}}$ ${\displaystyle X_{\rho (r)}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle L}$

${\displaystyle \Phi ^{+}:=\{r\in \Phi \mid {\text{ alle Koeffizienten in der Darstellung bzgl. der Basis }}\Phi _{0}{\text{ sind }}\geq 0\}}$, the positive roots

${\displaystyle \Phi ^{-}:=\Phi \setminus \Phi ^{+}}$, the negative roots

${\displaystyle U:=\langle X_{r}\mid r\in \Phi ^{+}\rangle }$, the subset of . ${\displaystyle \textstyle \bigcup _{r\in \Phi ^{+}}X_{r}}$ ${\displaystyle L(q^{i})}$

${\displaystyle V:=\langle X_{r}\mid r\in \Phi ^{-}\rangle }$

${\displaystyle M_{\sigma }:=\{x\in M\mid \sigma (x)=x\}}$, the set of fixed points of a subset . ${\displaystyle \sigma }$ ${\displaystyle M\subset L(q^{i})}$

${\displaystyle {}^{\mathrm {ord} \,\sigma }\!L(q^{i}):=\langle U_{\sigma },V_{\sigma }\rangle }$, the subset of . ${\displaystyle U_{\sigma }\cup V_{\sigma }}$ ${\displaystyle L(q^{i})}$

Since, by definition , is generated by the, is and natural and and therefore . In general, there is no equality here, hence the somewhat complicated definition. ${\displaystyle L(q^{i})}$ ${\displaystyle X_{r},r\in \Phi }$ ${\displaystyle L(q^{i})=\langle U,V\rangle }$ ${\displaystyle U_{\sigma }\subset L(q^{i})_{\sigma }}$ ${\displaystyle V_{\sigma }\subset L(q^{i})_{\sigma }}$ ${\displaystyle {}^{\mathrm {ord} \,\sigma }\!L(q^{i}):=\langle U_{\sigma },V_{\sigma }\rangle \subset L(q^{i})_{\sigma }}$

The groups are called twisted Chevalley groups . Since only the values ​​2 and 3 can be assumed and can only be of certain types with the restrictions mentioned above, you get the remaining groups of the above table overview, because the following sentence applies: ${\displaystyle {}^{\mathrm {ord} \,\sigma }\!L(q^{i})}$ ${\displaystyle \mathrm {ord} \,\sigma }$ ${\displaystyle L}$ ${\displaystyle {}^{2}\!A_{n}(q^{i}),{}^{2}\!B_{2}(2^{2m+1}),\ldots }$

The twisted Chevalley groups are simple with the exception of

${\displaystyle {}^{2}\!A_{2}(2^{2})}$, a resolvable group of order 72

${\displaystyle {}^{2}\!B_{2}(2)}$, a resolvable group of order 20

${\displaystyle {}^{2}\!G_{2}(3)}$, a 1,512-element group with an isomorphic commutator group of index 3 ${\displaystyle A_{1}(8)}$

${\displaystyle {}^{2}\!F_{4}(2)}$, a 35,942,400-element group with a commutator group of index 2.

The Tits Group

The twisted Chevalley groups are all simple except for the group with simple but whose commutator group has the 17,971,200 elements and is not isomorphic to any of the other groups listed so far. They are called the Tits Group after Jacques Tits . It belongs to the family of -groups of commutator groups of the first family, the members of which agree with their commutator groups for being simple non-Abelian groups. The second family consists exclusively of simple groups, all of which are of the Lie type except for the group . By definition, a finite simple group is called sporadic if it cannot be assigned to an infinite family of finite simple groups. Thus, the Tits group is not a sporadic group - even if it is not a Lie-type group. ${\displaystyle {}^{2}\!F_{4}(2^{2m+1})}$ ${\displaystyle {}^{2}\!F_{4}(2)}$ ${\displaystyle m=0.}$ ${\displaystyle {}^{2}\!F_{4}(2)^{'},}$ ${\displaystyle {}^{2}\!F_{4}(2^{2m+1})^{'}}$ ${\displaystyle m>0}$ ${\displaystyle {}^{2}\!F_{4}(2)^{'}}$

Individual evidence

1. ^ Michael Aschbacher: Finite Group Theory. Cambridge studies in advanced mathematics (2000), ISBN 0-521-78145-0 , table 16.1.
2. ^ Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9 , Chapter 13: The Twisted Simple Groups .
3. ↑ James E. Humphreys: Introduction to Lie Algebras and Representation Theory . Springer, Berlin / New York 1972, ISBN 0-387-90053-5 for a complete presentation of this theory.
4. ^ Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9 , Theorem 4.2.1.
5. ^ Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9 , chapter 4.3.
6. ^ Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9 , set 4.4.3.
7. ^ Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9 , Theorem 11.1.2.
8. ^ Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9 , sentences 12.2.3, 12.3.3 and 12.4.1.
9. ^ Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9 , Theorem 14.4.1.
10. ^ Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9 , comment on Theorem 14.4.1.