This article treats the term in a mathematical sense. For the biological meaning see
root (plant)
Root systems are used in mathematics as an aid to classifying the finite reflection groups and the finite dimensional, semi-simple complex Lie algebras .
Definitions
A subset of a vector space over a field of characteristic 0 is called a root system if it fulfills the following conditions:



-
 is finite.
is finite.
-
 is a linear generating system of .
is a linear generating system of .
- For each from there is a linear form with the following properties:



- For is .



- The linear mapping with maps on .




The elements of a root system are called roots.
A reduced root system is present if this also applies
- 4. If two roots are linearly dependent, then we have


One can show that the linear form from 3. is unique for each . It is called the co-root too ; the name is justified by the fact that the kowroots form a root system in the dual space . The image is a reflection and of course also clearly defined.





If and are two roots with , then one can show that also applies, and one calls and orthogonal to each other. If the root system can be written as a union of two non-empty subsets in such a way that every root in is orthogonal to every root in , then the root system is called reducible . In this case it can also be decomposed into a direct sum , so that and are root systems. If, on the other hand, a non-empty root system is not reducible, it is called irreducible .













The dimension of the vector space is called the rank of the root system. A subset of a root system is called a base if is a base of and every element of can be represented as an integral linear combination of elements of with exclusively positive or exclusively negative coefficients.







Two root systems and are accurate then another isomorphic if there is a Vektorraumisomorphismus with there.




Scalar product
One can define a scalar product with respect to which the images are reflections. In the reducible case, this can be put together from scalar products on the components. If, however, is irreducible, then this scalar product is unique up to one factor. You can normalize this so that the shortest roots have the length 1.



In principle, one can therefore assume that a root system “lives” in one (mostly ) with its standard scalar product. The integer of and then means a considerable restriction on the possible angles between two roots and . Because it results from







that must be an integer. Again, this is only the case for the angles 0 °, 30 °, 45 °, 60 °, 90 °, 120 °, 135 °, 150 °, 180 °. Only the angles 90 °, 120 °, 135 °, 150 ° are possible between two different roots of a base. All these angles actually occur, cf. the examples of rank 2. It also emerges that only a few values are possible for the length ratio of two roots in the same irreducible component.

Weyl group
The subgroup of the automorphism group of , which is generated by the amount of reflections , is called the Weyl group (after Hermann Weyl ) and is generally referred to as. With regard to the defined scalar product, all elements of the Weyl group are orthogonal, they are reflections .




The group operates faithful to and therefore is always finite. Furthermore, operates transitively on the set of bases of .




In the case , the levels of reflection divide the space into half-spaces, a total of several open convex subsets, the so-called Weyl chambers . This also operates transitively.



Positive roots, simple roots
After choosing a Weyl chamber , the set of positive roots can be defined by

-
 .
.
This defines an arrangement on through

-
 .
.
The positive and negative roots are those with and . (Note that this definition depends on the choice of the Weyl chamber. An arrangement is given for each Weyl chamber.)


A simple root is a positive root that cannot be broken down as the sum of several positive roots.
The simple roots form a base of . Every positive (negative) root can be decomposed as a linear combination of simple roots with non-negative ( non-positive ) coefficients.

Examples
The empty set is the only root system of rank 0 and is also the only root system that is neither reducible nor irreducible.
Except for isomorphism, there is only one reduced root system of rank 1. It consists of two roots that differ from 0 and is denoted by. If one also considers non-reduced root systems, the only other example is of rank 1.



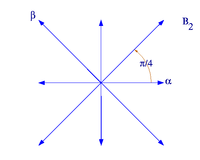
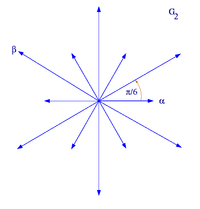
With the exception of isomorphism, all reduced root systems of rank 2 have one of the following forms. is a basis of the root system.


|

|
| Root system A 1 × A 1
|
Root system A 2
|
|
|
| Root system B 2
|
Root system G 2
|
reduced root systems of rank 2
In the first example ,, the ratio of the lengths of and is arbitrary, in the other cases, however, it is uniquely determined by the geometric conditions.



classification
Except for isomorphism , all information about a reduced root system is in its Cartan matrix

contain. This can also be shown in the form of a Dynkin diagram . To do this, one sets a point for each element of a base and connects the points α and β with lines, the number of which through

is determined. If there are more than one, a relation symbol> or <is also placed between the two points, i.e. H. an 'arrow' in the direction of the shorter root. The connected components of the Dynkin diagram correspond exactly to the irreducible components of the root system. As a diagram of an irreducible root system can only appear:
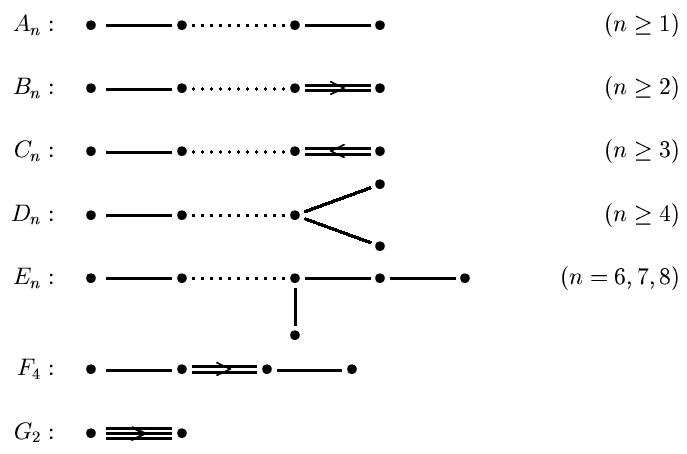
The index indicates the rank and thus the number of points in the diagram. Several identities for cases of lower order can be read from the Dynkin diagrams, namely:




That is why, for example, it only shows and only forms a separate class. The root systems belonging to series to are also referred to as classic root systems, the remaining five as exceptional or exceptional root systems . All the root systems mentioned also occur, for example, as the root system of semi-simple complex Lie algebras.






Not reduced root systems
For irreducible, unreduced root systems there are only a few possibilities that can be thought of as the union of one with one (with ) or as one in which for every short root its double has been added.




Other uses
Lie algebras
Let it be a finite-dimensional semi-simple Lie algebra and a Cartan subalgebra . Then a root is called if



![{\ mathfrak {g}} _ {\ alpha}: = \ left \ {Y \ in {\ mathfrak {g}}: \ left [X, Y \ right] = \ alpha ^ {\ vee} (X) Y \ \ forall X \ in {\ mathfrak {a}} \ right \} \ not = \ left \ {0 \ right \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfb6622af0b864644c8a171cada335c43ab8ed5d)
is. Here, the means of -killing form by



defined linear mapping.
Let be the set of roots, then it can be shown that


is a root system.
properties
This root system has the following properties:
-
 is a real form of .
is a real form of .
- For true if and only if .



- For everyone is .


- For all is , in particular .

![{\ mathfrak {g}} _ {{\ alpha + \ beta}} = \ left [{\ mathfrak {g}} _ {\ alpha}, {\ mathfrak {g}} _ {\ beta} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/122a1403ea30029443ca3a9940bfe5c24e40a822)
![{\ displaystyle \ left [{\ mathfrak {g}} _ {\ alpha}, {\ mathfrak {g}} _ {- \ alpha} \ right] \ subset {\ mathfrak {a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f17a26d24f09e537d0e84c290e37b44830aff87)
-
![{\ mathfrak {g}} _ {\ alpha}, {\ mathfrak {g}} _ {{- \ alpha}}, \ left [{\ mathfrak {g}} _ {\ alpha}, {\ mathfrak {g }} _ {{- \ alpha}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c853349c5cdee3222d5cdebe8ee5dd676d9e367) span a Lie algebra that is isomorphic to the Lie algebra sl (2, C) .
span a Lie algebra that is isomorphic to the Lie algebra sl (2, C) .
- For is , d. H. the root spaces are orthogonal with respect to the killing form . The restriction of the killing form to and is not degenerate. The restriction of the killing form to is real and positively definite.





Finite-dimensional semi-simple complex Lie algebras are classified by their root systems, i.e. by their Dynkin diagrams.
example
Be it . The Killing form is a Cartan subalgebra is the algebra of diagonal matrices with trace 0, ie . We denote the diagonal matrix with -th diagonal entry and the other diagonal entries equal 0.







The root system of is . Which is
too dual form



-
 .
.
As a positive Weyl Chamber you can

choose. The positive roots are then
-
 .
.
The simple roots are
-
 .
.
Reflection groups
A Coxeter group is abstractly defined as a group with a presentation

with and for , as well as the convention if has infinite order , d. H. there is no relation of form .






Coxeter groups are an abstraction of the concept of the mirror group .
Each Coxeter group corresponds to an undirected Dynkin diagram. The points in the diagram correspond to the producers . The and corresponding points are connected by edges.




Singularities
According to Wladimir Arnold , elementary catastrophes can be classified using Dynkin diagrams of the ADE type:
-
 - a non-singular point .
- a non-singular point .
-
 - a local extremum, either a stable minimum or an unstable maximum .
- a local extremum, either a stable minimum or an unstable maximum .
-
 - the fold, fold
- the fold, fold
-
 - the tip, cusp
- the tip, cusp
-
 - the swallowtail, swallowtail
- the swallowtail, swallowtail
-
 - the butterfly, butterfly
- the butterfly, butterfly
-
 - an infinite sequence of shapes in one variable
- an infinite sequence of shapes in one variable 
-
 - the elliptical umbilical catastrophe
- the elliptical umbilical catastrophe
-
 - the hyperbolic umbilical catastrophe
- the hyperbolic umbilical catastrophe
-
 - the parabolic umbilical catastrophe
- the parabolic umbilical catastrophe
-
 - an endless series of further umbilical disasters
- an endless series of further umbilical disasters
-
 - the Umbilical catastrophe
- the Umbilical catastrophe 


Web links
literature
- Jean-Pierre Serre: Complex Semisimple Lie Algebras , Springer, Berlin, 2001.








































































![{\ mathfrak {g}} _ {\ alpha}: = \ left \ {Y \ in {\ mathfrak {g}}: \ left [X, Y \ right] = \ alpha ^ {\ vee} (X) Y \ \ forall X \ in {\ mathfrak {a}} \ right \} \ not = \ left \ {0 \ right \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfb6622af0b864644c8a171cada335c43ab8ed5d)










![{\ mathfrak {g}} _ {{\ alpha + \ beta}} = \ left [{\ mathfrak {g}} _ {\ alpha}, {\ mathfrak {g}} _ {\ beta} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/122a1403ea30029443ca3a9940bfe5c24e40a822)
![{\ displaystyle \ left [{\ mathfrak {g}} _ {\ alpha}, {\ mathfrak {g}} _ {- \ alpha} \ right] \ subset {\ mathfrak {a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f17a26d24f09e537d0e84c290e37b44830aff87)
![{\ mathfrak {g}} _ {\ alpha}, {\ mathfrak {g}} _ {{- \ alpha}}, \ left [{\ mathfrak {g}} _ {\ alpha}, {\ mathfrak {g }} _ {{- \ alpha}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c853349c5cdee3222d5cdebe8ee5dd676d9e367)











































