Reflection (geometry)
In geometry , reflections are certain congruence images of the plane of the drawing or of ( Euclidean ) space. A sliding reflection is the combination of a reflection and a translation . In addition, there are oblique reflections that are not congruence images.
Point mirroring
It is an image that is given by a point Z (mirror point, center). The reflection at point Z assigns an image point P 'to each point P of the plane of the drawing or of space, which is determined by the fact that the connecting line [PP'] from point Z is bisected.
Sometimes the point reflection is also referred to as spatial reflection or inversion ; Note, however, that the term inversion is often used for another mapping, the reflection on a circle .
A point reflection has exactly one fixed point (that is, one point that the mapping leaves unchanged), namely the center Z. Fixed lines (i.e. the straight lines that the mapping transforms into itself) are exactly the straight lines through Z. Any straight line g becomes mapped onto a straight line (image line) g ′ parallel to g .
In the plane , the point reflection at the center Z is equivalent to a rotation by 180 ° around the center of rotation Z.
Point reflections are straight, length and angle true, i.e. congruence images .
Every plane point reflection can be replaced by two axis reflections executed one behind the other, the axes of these reflections going through the center Z and being perpendicular to one another. The order of these reflections is therefore arbitrary.
Every spatial point reflection can be replaced by three plane reflections executed one behind the other, the three mirror planes going through the center Z and being perpendicular to one another. The order of these reflections is therefore arbitrary.
In crystallography , a point reflection is called inversion or the point of inversion center and the axes are also called rotational inversion axes and are identified with the Hermann Mauguin symbol 1 .
Synthetic geometry
In synthetic geometry , point reflection can be defined in any affine translation plane that satisfies the (affine) Fano axiom . For this purpose, the center of the point reflection is firmly selected as the origin and the translation as a position "vector" is assigned to each point on the plane in a reversible manner . The point reflection is defined by and the following applies:
- For every point there is exactly one point reflection at this point,
- every point reflection is a partially true to ratio collineation , i.e. an affinity ,
- every point reflection is involutor ,
- the point reflection on is induced by the true-track endomorphism −1 of the translation group and therefore a centric stretching (→ see dilation ) with the stretching factor −1,
- in a pre-Euclidean level , the point reflections count among the congruence maps .
→ For the generalized terms used, see the article “ Affine translation plane ”, for a definition of point reflections in any affine planes that generalizes the definition given here, the article “ Fano's axiom ”.
Axis mirroring
An axis reflection (also straight line reflection) is given by a straight line a ( mirror axis or axis for short ). It assigns to each point P an image point P ', which is determined by the fact that the connecting line [PP'] is bisected at right angles by the axis a.
The fixed points of an axis reflection are exactly the points of a. One speaks therefore of the fixed point line a. The fixed lines of the axis reflection are exactly the axis a itself and all perpendicular lines to the axis. In the spatial case there are also fixed planes , namely the planes orthogonal to the axis a.
The axis mirroring is also a congruence mapping .
If there are two congruent objects in the plane, they can in any case be converted into one another by composition (chaining, sequential execution) of a maximum of three axis reflections. The axis mirroring can therefore be used as a basic concept of the metric geometry of the plane.
In the plane, it should be noted that an axis mirroring changes the orientation ( the direction of rotation) of a triangle. So here it is not an actual “movement”, that is, it cannot be realized by a physical movement without the object leaving the plane.
In three-dimensional space, the axis mirroring corresponds to a rotation of 180 ° around the mirror axis. An object that lies in one plane with the mirror axis is "flipped over" into the same plane; this is the movement that was not possible when constrained to one plane.
Synthetic geometry
In synthetic geometry , a (perpendicular) axis reflection is defined somewhat more generally for more general affine planes , the pre-Euclidean planes . Here we mean by the reflection on the straight line (the axis ) that mapping of the plane on to which each point that point assigns that on the perpendicular straight line to by is, and is determined by the fact that the intersection of these perpendicular straight line with the center of is . Compare the figure on the right: The angle is a right-hand angle , the marked vectors and are inverse to each other, that is, is the center of the line . As a result, the image is clearly defined from below the axis reflection .
The following applies to these vertical axis reflections:
- There is exactly one axis reflection for every straight line ,
- every axis reflection is a partially true to ratio collineation , i.e. an affinity ,
- Fixed points of the axis reflection are exactly the points of their axis,
- the fixed lines of an axis reflection are exactly the mirror axis and all straight lines perpendicular to it.
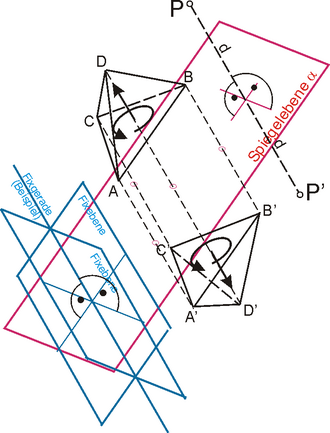
Plane mirroring
This further type of reflection only occurs in spatial geometry . It is given by a plane α, the mirror plane . The image point of P is determined by the fact that the connecting path between it and its image point P 'is bisected at right angles by the mirror plane.
Fixed points are exactly the points of the mirror plane. Fixed straight lines are the straight lines of the mirror plane and the straight lines that run orthogonally to it. Fixed planes are the mirror plane and the planes orthogonal to it.
The plane mirroring changes the orientation of a simplex ′ . So it is not an “actual” movement either: a tetrahedron cannot be physically converted into its mirror image.
In crystallography , the reflection is denoted by the Hermann Mauguin symbol m.
Reflections in rooms of any dimension
In an n-dimensional Euclidean space there are n types of reflections, namely reflections on 0, 1, ... (n-1) -dimensional subspaces ( mirror elements ).
Fixed points are always the points of the mirror element. Higher-dimensional fixed elements are its subspaces and the subspaces that are orthogonal to it.
The reflection at an (n-1) -dimensional subspace cannot be understood as an “actual movement” in the n-dimensional space. When embedded in an (n + 1) -dimensional space, it becomes synonymous with an involutorial rotation around the mirror element.
This means, among other things, that in the one-dimensional case (i.e. on a straight line) the point reflection is the only possible reflection, and that this, since it reverses the order of the points, cannot be understood as a movement without leaving the straight line.
See also
- Reflection Matrix (Linear Algebra)
- Reflection (descriptive geometry)
literature
- H. Schupp: Elementary Geometry . UTB Schöningh, 1977, ISBN 3-506-99189-2
-
Friedrich Bachmann : Structure of geometry from the concept of reflection. 2nd edition, Berlin; Göttingen; Heidelberg 1973
Summary: On the justification of geometry from the concept of reflection . In: Mathematische Annalen , Volume 123, 1951, pp. 341 ff. - Wendelin Degen, Lothar Profke: Fundamentals of affine and Euclidean geometry. Teubner, Stuttgart 1976, ISBN 3-519-02751-8 .
Web links
- Eric W. Weisstein : Mirroring . In: MathWorld (English).
Individual evidence
- ↑ W. Borchardt-Ott: Kristallographie: An introduction for natural scientists . Springer-Verlag, 2013, ISBN 978-3-662-08227-0 , pp. 39 ( books.google.de ).