Straight

Representation of straight lines in the Cartesian coordinate system

A straight line or short straight is an element of geometry . It is a straight, infinitely long, infinitely thin line that is unlimited in both directions. The shortest connection between two points , on the other hand, is called a line . However, modern axiomatic theories of geometry make no reference to it ( synthetic geometry ). For them, a straight line is an object with no internal properties, only the relationships to other straight lines, points and planes are important. In analytical geometry , a straight line is realized as a set of points. More precisely: In an affine space , a straight line is a one-dimensional affine subspace .

Synthetic geometry

In his elements , Euclid gave an explicit definition of a straight line that corresponds to the graphic image. However , this definition does not matter for sentences and their proofs . Modern axiom systems therefore dispense with such a definition.

In this case, a straight line is a term to which the individual axioms refer. An example is the first axiom from Hilbert's system of axioms :

Two different points and always define a straight line ${\ displaystyle P}$ ${\ displaystyle Q}$ ${\ displaystyle g}$ .

The meaning of the term straight line results from the totality of the axioms. An interpretation as an infinitely long, infinitely thin line is not mandatory, but only a suggestion of what one could clearly imagine by it.

In the projective level , the terms point and straight line are even completely interchangeable (duality) . This makes it possible to imagine a straight line as infinitely small and a point as infinitely long and infinitely thin.

Analytical geometry

Illustration of the support and direction vector

In analytic geometry , the geometric space is represented as a -dimensional vector space over the real numbers . A straight line is defined as a one-dimensional affine subspace of this vector space, i.e. H. as a secondary class of a one-dimensional linear subspace. ${\ displaystyle n}$

In three dimensions, the concept of straight lines in analytic geometry fulfills all the conditions that Hilbert presupposes in his system of axioms of geometry. In this case, a straight line is therefore also a straight line in the Hilbert sense.

You only need the position of two points to describe a straight line. One of the points serves as a “support” for the straight line, it “rests” on it, so to speak - this point is therefore called the starting point or support point of the straight line. The second point gives the direction of the straight line. The direction is indicated by the vector from the reference point to the "direction point".

The straight line through the points and contains exactly those points whose position vector is a representation ${\ displaystyle g}$ ${\ displaystyle P}$ ${\ displaystyle Q}$ ${\ displaystyle X}$ ${\ displaystyle {\ vec {x}}}$

{\ displaystyle {\ vec {x}} = {\ overrightarrow {OP}} + t \, {\ overrightarrow {PQ}}}

With

{\ displaystyle t \ in \ mathbb {R}}

owns, so

{\ displaystyle g = \ {X \ mid {\ overrightarrow {OX}} = {\ overrightarrow {OP}} + t \, {\ overrightarrow {PQ}}; t \ in \ mathbb {R} \}.}

Here is the support vector, that is, the position vector of the support point and the direction vector . ${\ displaystyle {\ overrightarrow {OP}}}$ ${\ displaystyle P}$ ${\ displaystyle {\ overrightarrow {PQ}}}$

The affine hull of two different vectors and ${\ displaystyle {\ vec {v}}}$ ${\ displaystyle {\ vec {w}}}$

{\ displaystyle \ {\ lambda {\ vec {v}} + \ mu {\ vec {w}} \ mid \ lambda, \ mu \ in \ mathbb {R}, \ lambda + \ mu = 1 \}}

is also a straight line.

The solution space of an (inhomogeneous) linear system of equations with linearly independent equations is also an affine subspace of dimension one and thus a straight line. In two dimensions, a straight line can be represented by a straight line equation ${\ displaystyle n-1}$

{\ displaystyle \ alpha x + \ beta y = \ gamma}

specified, where and or must be non-zero. If it is not equal to 0, one speaks of a linear function . ${\ displaystyle \ alpha, \ beta, \ gamma \ in \ mathbb {R}}$ ${\ displaystyle \ alpha}$ ${\ displaystyle \ beta}$ ${\ displaystyle \ beta}$ ${\ displaystyle y = f (x)}$

Shortest way

In real Euclidean space the shortest path between two points is on a straight line. If one generalizes this property of the straight line on curved spaces ( manifolds ), one arrives at the concept of the geodesic line, in short geodesic .

Equation of a straight line in the plane

The equation of a straight line in the plane can be determined in three different ways:

Point-direction equation:

A point and the angle of inclination (angle of rise) are given .

{\ displaystyle P_ {0} (x_ {0} | y_ {0})}

{\ displaystyle \ alpha}

{\ displaystyle y = y_ {0} + \ tan (\ alpha) \ cdot (x-x_ {0})}

Given a point and the slope (the slope) . ${\ displaystyle P_ {0} (x_ {0} | y_ {0})}$ ${\ displaystyle m}$
${\ displaystyle y = y_ {0} + m \ cdot (x-x_ {0})}$

Two point equation:

There are two points and with . ${\ displaystyle P_ {1} (x_ {1} | y_ {1})}$ ${\ displaystyle P_ {2} (x_ {2} | y_ {2})}$ ${\ displaystyle x_ {1} \ neq x_ {2}}$
${\ displaystyle y = y_ {1} + {\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}} \ cdot (x-x_ {1})}$

or

{\ displaystyle y = y_ {1} {\ frac {x-x_ {2}} {x_ {1} -x_ {2}}} + y_ {2} {\ frac {x-x_ {1}} {x_ {2} -x_ {1}}}}

Equation of a straight line in space ℝⁿ

Point-direction equation

For each pair of a position vector (i.e. point) and a direction vector, there is a straight line which contains and runs in the direction , namely ${\ displaystyle (\ mathbf {p}, \ mathbf {r})}$ ${\ displaystyle \ mathbf {p} \ in \ mathbb {R} ^ {n}}$ ${\ displaystyle \ mathbf {r} \ in \ mathbb {R} ^ {n} \ setminus \ {0 \}}$ ${\ displaystyle g}$ ${\ displaystyle \ mathbf {p}}$ ${\ displaystyle \ mathbf {r}}$

{\ displaystyle g = \ {\ mathbf {p} + \ lambda \ mathbf {r} \ mid \ lambda \ in \ mathbb {R} \}}

.

Two point equation

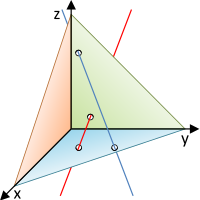
Let two position vectors (i.e. points) be given with . Then there is a uniquely determined straight line that contains and , namely ${\ displaystyle \ mathbf {p} _ {1}, \ mathbf {p} _ {2} \ in \ mathbb {R} ^ {n}}$ ${\ displaystyle \ mathbf {p} _ {1} \ neq \ mathbf {p} _ {2}}$ ${\ displaystyle g}$ ${\ displaystyle \ mathbf {p} _ {1}}$ ${\ displaystyle \ mathbf {p} _ {2}}$

{\ displaystyle g = \ {\ mathbf {p} _ {1} + \ lambda (\ mathbf {p} _ {2} - \ mathbf {p} _ {1}) \ mid \ lambda \ in \ mathbb {R } \} = \ {(1- \ lambda) \ mathbf {p} _ {1} + \ lambda \ mathbf {p} _ {2} \ mid \ lambda \ in \ mathbb {R} \}}

.

Position of two straight lines to one another

Positional relationships of two straight lines (red and dark blue) in space
true parallel (left) and equal (right)
cutting (in the black point)
crooked

Two straight lines can have the following positional relationships to one another. You can:

Be the same: Both lines have all points in common.
Have an intersection: Both straight lines have exactly one point in common (especially: perpendicular to each other).
Really parallel to each other: Both straight lines have no point in common and can be converted into each other by shifting.
Being skewed to one another: Both straight lines have no point in common, but cannot be converted into one another by a shift alone (from at least three dimensions ).

In the sense of the theory of relations , one speaks of parallelism when both lines are identical; in particular, each line is parallel to itself. To be more precise, a distinction is then made between genuinely parallel and identical .

The straight line in technology and surveying

In technical fields, the straight line is the most important element for constructions , for routing , for location determination and for measuring coordinates :

in the form of two legs when measuring angles ,
for measuring directions (north or relative)
for distance measurement
for alignments and for staking out lines.

During measurements it is represented by the sighting axis of a measuring telescope or a laser , in construction it is represented by a batter board .

Web links

Commons : Straight - collection of pictures, videos and audio files

Wiktionary: Straight - explanations of meanings, word origins, synonyms, translations

Eric W. Weisstein : Line . In: MathWorld (English).