Affine subspace

This article deals with an affine subspace of a vector space. To affine subspaces of an affine point space see Affiner room .

A plane in three-dimensional space (blue) is an affine subspace that results from shifting an original plane by a vector (red).

In linear algebra , an affine subspace of a vector space is a subset that arises from a subspace by shifting . Such an affine subspace is also an affine space in the sense of analytic geometry.

definition

A subset of a vector space is called an affine subspace if there is a vector from and a subspace of such that ${\displaystyle A}$ ${\displaystyle V}$ ${\displaystyle v}$ ${\displaystyle V}$ ${\displaystyle U_{A}}$ ${\displaystyle V}$

${\displaystyle A=v+U_{A}=\left\{v+u\mid u\in U_{A}\right\}}$

applies. In this case, the support vector of and is also called the associated linear subspace (the connection vectors ). is clearly determined by; all with are support vectors of . The dimension of is the dimension of . ${\displaystyle v}$ ${\displaystyle A}$ ${\displaystyle U_{A}}$ ${\displaystyle A}$ ${\displaystyle U_{A}}$ ${\displaystyle A}$ ${\displaystyle w\in V}$ ${\displaystyle v-w\in U_{A}}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle U_{A}}$

A one-dimensional affine subspace is called an affine line . A two-dimensional affine subspace is called an affine plane .

If the linear subspace belonging to an affine subspace has the codimension , it is called an affine hyperplane . ${\displaystyle A}$ ${\displaystyle U_{A}}$ ${\displaystyle 1}$ ${\displaystyle A}$

In analytic geometry the empty set is sometimes referred to as an affine subspace. It then has the dimension as an affine space and no linear subspace is assigned to it. ${\displaystyle \dim \emptyset =-1}$

Clear viewing

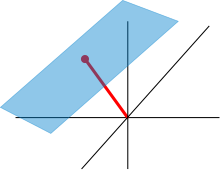
As subspace a'll origin line in three-dimensional vector space chosen for which: ${\displaystyle U}$ ${\displaystyle \mathbb {R} ^{3}}$

${\displaystyle g:\ {\vec {x}}=\lambda \ {\begin{pmatrix}0\\0\\1\end{pmatrix}}}$ With ${\displaystyle \lambda \in \mathbb {R} }$

As a vector becomes ${\displaystyle {\vec {v}}\in V}$

${\displaystyle {\vec {v}}={\begin{pmatrix}1\\0\\0\end{pmatrix}}}$

elected. Then the affine subspace is a straight line that is shifted by (i.e. by one unit in the -direction) from the origin, with the equation: ${\displaystyle A=v+U}$ ${\displaystyle (1|0|0)}$ ${\displaystyle x}$

${\displaystyle h:\ {\vec {x}}={\begin{pmatrix}1\\0\\0\end{pmatrix}}+\mu \ {\begin{pmatrix}0\\0\\1\end{pmatrix}}}$ With ${\displaystyle \mu \in \mathbb {R} }$

The displaced straight line that results in this way is an affine subspace, but not a subspace of V, since it does not contain the zero vector .

Dimension formula for affine subspaces

Let be a finite-dimensional vector space over a field and let two affine subspaces of . ${\displaystyle V}$ ${\displaystyle K}$ ${\displaystyle A,B}$ ${\displaystyle V}$

In the event that and are not disjoint or one of the two spaces is empty, the dimensional formula applies: ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle \dim(A)+\dim(B)=\dim(A\vee B)+\dim(A\cap B)}$

However, if and are disjoint and not empty, the dimension formula is ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle \dim(A)+\dim(B)=\dim(A\vee B)+\dim(U_{A}\cap U_{B})-1,}$

where is obtained from the representation (with a fixed and the associated linear subspace of ). Analogously one obtains . ${\displaystyle U_{A}}$ ${\displaystyle A=v+U_{A}}$ ${\displaystyle v\in A}$ ${\displaystyle U_{A}}$ ${\displaystyle V}$ ${\displaystyle U_{B}}$

In both cases stands for the connecting space of and . ${\displaystyle A\vee B}$ ${\displaystyle A}$ ${\displaystyle B}$

properties

Since one can also choose in the definition of an affine subspace , every subspace is at the same time an affine subspace. An affine subspace is a subspace if and only if it contains the zero vector. ${\displaystyle v=0}$

The solution space of an inhomogeneous system of linear equations in variables over the body is an affine subspace of if the solution set is not empty. Every affine subspace can be described by such a system of equations. Alternatively, an affine subspace can also be specified as an affine envelope of vectors or, as follows directly from the definition, with the help of a support vector and a basis of the subspace. ${\displaystyle n}$ ${\displaystyle K}$ ${\displaystyle K^{n}}$

literature

• Gerd Fischer : Linear Algebra. ISBN 3-528-03217-0 , p. 166 ff. ( Excerpt (Google) }).
• Siegfried Bosch : Linear Algebra. ISBN 978-3-540-76437-3 , p. 65 ff.