
Representation of two skewed straight lines

Spatial image of two skewed straight lines with a common perpendicular
In geometry two straight lines are called skewed if they neither intersect nor are parallel to each other. This is not possible in two-dimensional space , since here all conceivable straight lines lie in the same plane and intersect or are parallel. Crooked lines therefore only exist in at least three-dimensional spaces.
To demonstrate that two straight lines and are skewed, it suffices to show that a direction vector of a direction vector of and a displacement vector of a point on a point on linearly independent are. Equivalently, one can show that there is no plane that contains both straight lines.






Calculation of the distance between two skewed straight lines
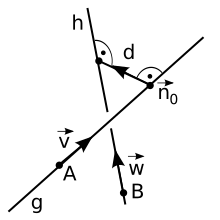
Distance d between two skewed straight lines
The uniquely determined distance of the smallest length that connects two crooked straight lines and is called the common perpendicular of the two straight lines. The straight line on which the common perpendicular lies is called the minimum transversal of the two straight lines. This is the uniquely determined straight line which is at right angles to the two straight lines. The length of the common perpendicular of and is the distance between the two straight lines.





Given are the skewed straight lines and with the support points and or the support vectors and the direction vectors and . Then the parameter forms are the straight line equations








-
 ,
,
where applies and the three vectors must be linearly independent.


The normal vector , which is perpendicular to the two direction vectors and , can be calculated using the cross product :



-
 and bring to the length 1: .
and bring to the length 1: .
The calculation of the distance is possible through the orthogonal projection of the connection vector of the support points onto the normal vector. For this purpose, the normal vector is brought to length 1. The distance between the two crooked straight lines is then
-
 .
.
Notation with determinants
The two straight line equations are written out
![{\ displaystyle g \ colon {\ vec {x}} = \ left ({\ begin {smallmatrix} a_ {1} \\ [0.7ex] a_ {2} \\ [0.7ex] a_ {3} \ end { smallmatrix}} \ right) + r \ left ({\ begin {smallmatrix} v_ {1} \\ [0.7ex] v_ {2} \\ [0.7ex] v_ {3} \ end {smallmatrix}} \ right) }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3160bfc87366a2eac81e4665f233f44189958a4)
-
![{\ displaystyle h \ colon {\ vec {x}} = \ left ({\ begin {smallmatrix} b_ {1} \\ [0.7ex] b_ {2} \\ [0.7ex] b_ {3} \ end { smallmatrix}} \ right) + s \ left ({\ begin {smallmatrix} w_ {1} \\ [0.7ex] w_ {2} \\ [0.7ex] w_ {3} \ end {smallmatrix}} \ right) \ \ \, r, s \ in \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e993c87603d44aa990413dee0130fdc4c25de39e) .
.
The distance between the two skewed straight lines using the determinant det is then
-
 .
.
Determination of the plumb points

Drawing for determining the plumb points
The plumb point is obtained by setting up an auxiliary plane . The point lies on the auxiliary plane and spans the auxiliary plane.





-
 ,
,
where the normal vector is determined by
-
 .
.
The intersection of and results in the plumb line :



-
 With
With 
Similarly, with the plane and its intersection with :



-
 With
With 
With this method, the distance does not have to be calculated.

The plumb bob points can also be determined in such a way that the two (initially unknown) points are attached:
-
 and
and 
and then slide one along and make it coincide with the other:

-
 .
.
A line by line resolution results in a system with three variables: , and . The base points are then:



-
 and .
and .
The distance results from

comment
literature
- M. Jeger, B. Eckmann : Introduction to vector geometry and linear algebra for engineers and natural scientists . Birkhäuser Verlag, Basel / Stuttgart 1967.
- Joachim Köhler et al .: Analytical geometry and imaging geometry in vector representation . Diesterweg-Verlag, Frankfurt am Main 1971, ISBN 3-425-05302-7
- Joachim Köhler et al .: Analytical geometry and imaging geometry in vector representation . Diesterweg-Verlag, Frankfurt am Main 1971, ISBN 3-425-05302-7
- Wilmut Kohlmann et al .: Linear Algebra and Analytical Geometry . Vieweg-Verlag, Braunschweig 1977, ISBN 3-594-10826-0
- Elisabeth and Friedrich Barth, Gert Krumbacher: Descriptive analytical geometry . Oldenbourg-Verlag, Munich 1997, ISBN 3-486-03500-2
Web links
Individual evidence
-
↑ Meyers computing Duden , Bibliographical Institute, Mannheim, 1960, p 807
-
↑ Section 3.3.1.1 Two straight lines in the Google books search for the paperback of mathematics



















![{\ displaystyle g \ colon {\ vec {x}} = \ left ({\ begin {smallmatrix} a_ {1} \\ [0.7ex] a_ {2} \\ [0.7ex] a_ {3} \ end { smallmatrix}} \ right) + r \ left ({\ begin {smallmatrix} v_ {1} \\ [0.7ex] v_ {2} \\ [0.7ex] v_ {3} \ end {smallmatrix}} \ right) }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3160bfc87366a2eac81e4665f233f44189958a4)
![{\ displaystyle h \ colon {\ vec {x}} = \ left ({\ begin {smallmatrix} b_ {1} \\ [0.7ex] b_ {2} \\ [0.7ex] b_ {3} \ end { smallmatrix}} \ right) + s \ left ({\ begin {smallmatrix} w_ {1} \\ [0.7ex] w_ {2} \\ [0.7ex] w_ {3} \ end {smallmatrix}} \ right) \ \ \, r, s \ in \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e993c87603d44aa990413dee0130fdc4c25de39e)




















