Intersection

This article applies to intersections in mathematics. For points of intersection in the descriptive geometry, see Intersection (Descriptive Geometry) .

In mathematics, an intersection point is a common point between two curves in a plane or in space. In general usage, the point of intersection is that of two straight lines , which is, however, contained in the mathematical term “curve”. In space there is also the intersection of a curve with a surface . In the simplest case, a straight line intersects a plane.

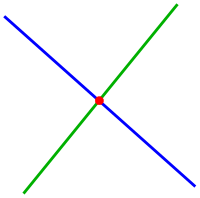
Intersection of two straight lines

The determination of a point of intersection is easy in both cases of straight line and straight line (see below). In general, the determination of points of intersection leads to non-linear equations that can be solved in practice using a Newton method . Intersections of a straight line with a conic section (circle, hyperbola, ellipse, parabola) or a quadric (sphere, ellipsoid, hyperboloid, ...) lead to quadratic equations and are relatively easy to solve. For the intersection of a straight line with a plane / sphere / cylinder / cone, the representational geometry offers methods to determine points of intersection graphically .

Intersection in the plane

Intersection of two straight lines

For the intersection of two non-parallel

• Straight lines (given in coordinate form ) ${\displaystyle a_{1}x+b_{1}y=c_{1},\ a_{2}x+b_{2}y=c_{2}}$

results from Cramer's rule for the coordinates of the point of intersection ${\displaystyle (x_{s},y_{s})}$

${\displaystyle x_{s}={\frac {c_{1}b_{2}-c_{2}b_{1}}{a_{1}b_{2}-a_{2}b_{1}}},\quad y_{s}={\frac {a_{1}c_{2}-a_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}}.\ }$

If is, the two straight lines are parallel. ${\displaystyle a_{1}b_{2}-a_{2}b_{1}=0}$

• For a straight line through the points

${\displaystyle P_{1}={\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}}}$ and ${\displaystyle P_{2}={\begin{pmatrix}x_{2}\\y_{2}\end{pmatrix}}}$

and a straight line through the points

${\displaystyle P_{3}={\begin{pmatrix}x_{3}\\y_{3}\end{pmatrix}}}$ and ${\displaystyle P_{4}={\begin{pmatrix}x_{4}\\y_{4}\end{pmatrix}}}$

The point of intersection is calculated by converting the two-point forms into coordinate forms beforehand.

The intersection results in ${\displaystyle S={\begin{pmatrix}x_{s}\\y_{s}\end{pmatrix}}}$

${\displaystyle x_{s}={\frac {(x_{4}-x_{3})(x_{2}y_{1}-x_{1}y_{2})-(x_{2}-x_{1})(x_{4}y_{3}-x_{3}y_{4})}{(y_{4}-y_{3})(x_{2}-x_{1})-(y_{2}-y_{1})(x_{4}-x_{3})}}}$

and

${\displaystyle y_{s}={\frac {(y_{1}-y_{2})(x_{4}y_{3}-x_{3}y_{4})-(y_{3}-y_{4})(x_{2}y_{1}-x_{1}y_{2})}{(y_{4}-y_{3})(x_{2}-x_{1})-(y_{2}-y_{1})(x_{4}-x_{3})}}}$

Intersection of two lines

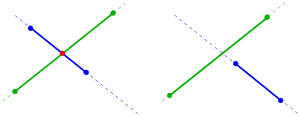
Intersection of two lines

If two non-parallel lines and are given, they do not have to intersect. Because the intersection of the associated straight line does not have to be included in both segments. To clarify the latter, both routes are represented parameterized: ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2})}$ ${\displaystyle (x_{3},y_{3}),(x_{4},y_{4})}$ ${\displaystyle (x_{0},y_{0})}$

${\displaystyle (x(s),y(s))=(x_{1}+s(x_{2}-x_{1}),y_{1}+s(y_{2}-y_{1}))}$,

${\displaystyle (x(t),y(t))=(x_{3}+t(x_{4}-x_{3}),y_{3}+t(y_{4}-y_{3}))\ .}$

If the lines intersect, the common point of the associated straight line must have parameters with the property . The cutting parameters are the solution of the linear system of equations ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle s_{0},t_{0}}$ ${\displaystyle 0\leq s_{0},t_{0}\leq 1}$ ${\displaystyle s_{0},t_{0}}$

${\displaystyle s(x_{2}-x_{1})-t(x_{4}-x_{3})=x_{3}-x_{1},}$

${\displaystyle s(y_{2}-y_{1})-t(y_{4}-y_{3})=y_{3}-y_{1}\ .}$

This is solved (as above) with Cramer's rule, the intersection condition is checked and or is inserted into the associated parameter representation in order to finally obtain the intersection point . ${\displaystyle 0\leq s_{0}\leq 1,\ 0\leq t_{0}\leq 1}$ ${\displaystyle s_{0}}$ ${\displaystyle t_{0}}$ ${\displaystyle (x_{0},y_{0})}$

Example: For the distances and the system of equations is obtained ${\displaystyle (1,1),(3,2)}$ ${\displaystyle (1,4),(2,-1)}$

${\displaystyle 2s-t=0}$

${\displaystyle s+5t=3}$

and . I.e. the lines intersect and the intersection is . ${\displaystyle s_{0}={\tfrac {3}{11}},t_{0}={\tfrac {6}{11}}}$ ${\displaystyle ({\tfrac {17}{11}},{\tfrac {14}{11}})}$

Note: If you consider straight lines through two pairs of points (not segments!), You can ignore the condition and obtain the intersection of the two straight lines with this method (see previous section). ${\displaystyle 0\leq s_{0},t_{0}\leq 1}$

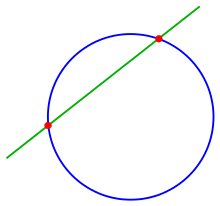
Section of a straight line

Intersections of a straight line with a circle

To cut the

• Straight with the circle ${\displaystyle ax+by=c}$ ${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}=r^{2}}$

the system is first shifted by setting and so that the center of the circle is at the zero point. This results in a new circular equation ${\displaystyle {\bar {x}}=x-x_{0}}$ ${\displaystyle {\bar {y}}=y-y_{0}}$

${\displaystyle {\bar {x}}^{2}+{\bar {y}}^{2}=r^{2}}$

and as a new straight line equation

${\displaystyle a{\bar {x}}+b{\bar {y}}=d}$with . ${\displaystyle d=c-ax_{0}-by_{0}}$

By solving the straight line equation according to or , inserting it into the circular equation, applying the solution formula for quadratic equations and then undoing the shift, the intersection points are obtained with ${\displaystyle {\bar {x}}}$ ${\displaystyle {\bar {y}}}$ ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2})}$

${\displaystyle x_{1/2}=x_{0}+{\frac {ad\pm b{\sqrt {r^{2}(a^{2}+b^{2})-d^{2}}}}{a^{2}+b^{2}}},\quad y_{1/2}=y_{0}+{\frac {bd\mp a{\sqrt {r^{2}(a^{2}+b^{2})-d^{2}}}}{a^{2}+b^{2}}}\ ,}$

if applicable. In the case of equality, there is only one point of intersection and the straight line is a tangent to the circle. ${\displaystyle r^{2}(a^{2}+b^{2})\geq d^{2}}$

Note: The intersection points of a straight line with a parabola or a hyperbola can be determined analogously by solving a quadratic equation.

Intersection of two circles

Determining the intersection of two circles

• ${\displaystyle (x-x_{1})^{2}+(y-y_{1})^{2}=r_{1}^{2},\ \quad (x-x_{2})^{2}+(y-y_{2})^{2}=r_{2}^{2}}$

the problem of intersections of the straight line ( power line ) can be solved by subtracting the two equations

${\displaystyle 2(x_{2}-x_{1})x+2(y_{2}-y_{1})y=r_{1}^{2}-x_{1}^{2}-y_{1}^{2}-r_{2}^{2}+x_{2}^{2}+y_{2}^{2}}$

lead back with one of the two circles (see above).

Intersection of two circles, centers on the x-axis, power line dark red

Special case  : ${\displaystyle \;x_{1}=y_{1}=y_{2}=0}$
In this case the first circle has the zero point as the center and the second center is on the x-axis. This simplifies the equation of the power line and results for the intersection points ${\displaystyle \;2x_{2}x=r_{1}^{2}-r_{2}^{2}+x_{2}^{2}\;}$ ${\displaystyle (x_{0},\pm y_{0})}$

${\displaystyle x_{0}={\frac {r_{1}^{2}-r_{2}^{2}+x_{2}^{2}}{2x_{2}}},\quad y_{0}={\sqrt {r_{1}^{2}-x_{0}^{2}}}\ .}$

If there is, the circles do not intersect. In the case , the circles touch. ${\displaystyle r_{1}^{2}<x_{0}^{2}}$ ${\displaystyle r_{1}^{2}=x_{0}^{2}}$

The general case can always be reduced to this special case by a suitable shift and rotation.

Alternative calculation method

Analogous to the circle equations above , the center points of the circles can be described as follows:

Intersection of two circles

${\displaystyle {\boldsymbol {M}}_{1}={\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}}\quad \quad {\boldsymbol {M}}_{2}={\begin{pmatrix}x_{2}\\y_{2}\end{pmatrix}}}$

The designations can be found in the adjacent graphic. Furthermore, the vector and can be described as follows: ${\displaystyle {\boldsymbol {D}}_{1}}$ ${\displaystyle {\boldsymbol {D}}_{2}}$

${\displaystyle {\boldsymbol {D}}_{1}={\begin{pmatrix}D_{1x}\\D_{1y}\end{pmatrix}}={\frac {1}{2}}\cdot \left({\frac {r_{1}^{2}-r_{2}^{2}}{\left\|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\right\|^{2}}}+1\right)\cdot \left({\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\right)}$

${\displaystyle {\boldsymbol {D}}_{2}={\begin{pmatrix}D_{2x}\\D_{2y}\end{pmatrix}}={\frac {1}{2}}\cdot \left({\frac {r_{2}^{2}-r_{1}^{2}}{\left\|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\right\|^{2}}}+1\right)\cdot \left({\boldsymbol {M}}_{1}-{\boldsymbol {M}}_{2}\right)}$

(Note: represents the vector norm or the length of the vector) ${\displaystyle \|\cdot \|}$

Where represent the radii of the circles. So this vector connects the points and . This formula is arrived at through geometrical considerations. With the triangles in the graphic, the following equation must be fulfilled according to the Pythagorean Theorem . ${\displaystyle r_{1},r_{2}}$ ${\displaystyle {\boldsymbol {M}}_{1}}$ ${\displaystyle {\boldsymbol {M}}_{12}}$

${\displaystyle l={\sqrt {r_{1}^{2}-\|{\boldsymbol {D}}_{1}\|^{2}}}={\sqrt {r_{2}^{2}-\|{\boldsymbol {D}}_{2}\|^{2}}}\quad \quad (1)}$

Furthermore, the sum of the lengths of and the distance between the centers of the circles corresponds to: ${\displaystyle {\boldsymbol {D}}_{1}}$ ${\displaystyle {\boldsymbol {D}}_{2}}$

${\displaystyle \|{\boldsymbol {D}}_{1}\|+\|{\boldsymbol {D}}_{2}\|=\|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\|}$

As a result, the center-to-center distance can be divided into the lengths of and as a percentage with the parameter : ${\displaystyle x}$ ${\displaystyle {\boldsymbol {D}}_{1}}$ ${\displaystyle {\boldsymbol {D}}_{2}}$

${\displaystyle \|{\boldsymbol {D}}_{1}\|=x\cdot \|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\|\quad ,\quad \|{\boldsymbol {D}}_{2}\|=(1-x)\cdot \|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\|\quad \quad (2)}$

With the equations (1) and (2) the parameter can be determined: ${\displaystyle x}$

${\displaystyle r_{1}^{2}-x^{2}\cdot \|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\|^{2}=r_{2}^{2}-(1-x)^{2}\cdot \left\|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\right\|^{2}\quad \rightarrow \quad x={\frac {1}{2}}\cdot \left({\frac {r_{1}^{2}-r_{2}^{2}}{\left\|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\right\|^{2}}}+1\right)}$

Now we need a unit vector orthogonal to the direction vector between and . This can then be represented as follows: ${\displaystyle {\boldsymbol {M}}_{1}}$ ${\displaystyle {\boldsymbol {M}}_{2}}$

${\displaystyle {\boldsymbol {e}}_{2}={\begin{pmatrix}-e_{1y}\\e_{1x}\end{pmatrix}}\quad {\text{mit}}\quad {\boldsymbol {e}}_{1}={\begin{pmatrix}e_{1x}\\e_{1y}\end{pmatrix}}={\frac {{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}}{\|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\|}}}$

The intersections can now be described as follows: ${\displaystyle {\boldsymbol {x_{s}}}}$

${\displaystyle {\boldsymbol {x}}_{s}={\boldsymbol {M}}_{1}+{\boldsymbol {D}}_{1}\pm l\cdot {\boldsymbol {e}}_{2}={\boldsymbol {M}}_{2}+{\boldsymbol {D}}_{2}\pm l\cdot {\boldsymbol {e}}_{2}\quad {\text{unter der Bedingung}}\quad \left\|{\boldsymbol {M}}_{2}-{\boldsymbol {M}}_{1}\right\|\leq r_{1}+r_{2}}$

Section circle-ellipse

Intersections of two conic sections

The task of determining the points of intersection of an ellipse / hyperbola / parabola with an ellipse / hyperbola / parabola generally leads to an equation of the fourth degree when a coordinate is eliminated , which can only be easily solved in special cases. The intersection points can, however, also be determined iteratively with the help of the 1- or 2-dimensional Newton method , depending on whether a) both conic sections are implicitly represented (→ 2-dimensional Newton) or b) one is implicitly represented and the other is parameterized (→ 1-dim. Newton). See the next section.

Intersection of two curves

Intersection of two curves: transversal cutting

Intersection of two curves: touching cutting or contact

Two continuously differentiable curves lying in the plane (ie curves without a “kink”) have an intersection point if they have a point in the plane in common and the two curves either at this point ${\displaystyle \mathbb {R} ^{2}}$

a) have different tangents ( transverse cutting ), or

b) have common tangents and intersect at the point ( touching cutting , see picture).

If the two curves have a common point and a common tangent there, but do not cross, they touch at . ${\displaystyle S}$ ${\displaystyle S}$

Since contact cutting rarely occurs and is mathematically very complex to deal with, transversal cutting is always assumed in the following . In order not to have to mention it again and again, the respective necessary differentiability conditions are also assumed. The determination of intersection points repeatedly leads to the problem of having to solve an equation with one or two equations with two unknowns. The equations are generally not linear and can then be solved numerically, for example using the 1- or 2-dimensional Newton method . The individual cases and the equations to be solved are described below:

Intersection: parameterized curve / implicit curve

Intersection: implicit curve / implicit curve

• If both curves are explicitly present: equating gives the equation ${\displaystyle y=f_{1}(x),\ y=f_{2}(x)}$

${\displaystyle f_{1}(x)=f_{2}(x)\ .}$

• If both curves parameterized available: . ${\displaystyle K_{1}:(x_{1}(t),y_{1}(t)),\ K_{2}:(x_{2}(s),y_{2}(s))}$

Equating gives two equations for two unknowns:

${\displaystyle x_{1}(t)=x_{2}(s),\ y_{1}(t)=y_{2}(s)\ .}$

• If a curve parameterized and the other implicitly exist: . ${\displaystyle K_{1}:(x_{1}(t),y_{1}(t)),\ K_{2}:f(x,y)=0}$

This is the simplest case after the explicit one. Because you only have to insert the parametric representation of into the equation of and you get the equation ${\displaystyle K_{1}}$ ${\displaystyle f(x,y)=0}$ ${\displaystyle K_{2}}$

${\displaystyle f(x_{1}(t),y_{1}(t))=0\ .}$

• If both curves implicitly exist: . ${\displaystyle K_{1}:f_{1}(x,y)=0,\ K_{2}:f_{2}(x,y)=0}$

An intersection here is the solution of the generally non-linear system of equations

${\displaystyle f_{1}(x,y)=0,\ f_{2}(x,y)=0\ .}$

The starting values ​​required for the respective Newton method can be obtained from a visualization of the two curves. A parameterized or explicitly given curve can be easily visualized because a point can be calculated for a given parameter or directly. For curves given implicitly this is not so easy. Here one generally has to calculate curve points with the help of starting points and an iteration process. ${\displaystyle t}$ ${\displaystyle x}$

Examples:

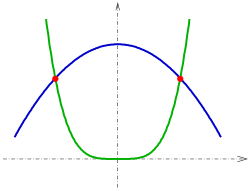
1: and circle (see picture). ${\displaystyle K_{1}:(t,t^{3})}$ ${\displaystyle K_{2}:(x-1)^{2}+(y-1)^{2}-10=0}$

It's the Newton iteration for ${\displaystyle t_{n+1}:=t_{n}-{\frac {f(t_{n})}{f'(t_{n})}}}$

${\displaystyle f(t)=(t-1)^{2}+(t^{3}-1)^{2}-10}$ perform. You can choose −1 and 1.5 as starting values.

The intersections are: (−1.1073; −1.3578) and (1.6011; 4.1046)

2: ${\displaystyle K_{1}:f_{1}(x,y)=x^{4}+y^{4}-1=0,}$

${\displaystyle K_{2}:f_{2}(x,y)=(x-0.5)^{2}+(y-0.5)^{2}-1=0}$ (see picture).

It's the Newton iteration

${\displaystyle {x_{n+1} \choose y_{n+1}}={x_{n}+\delta _{x} \choose y_{n}+\delta _{y}}}$perform, solving the linear system of equations ${\displaystyle {\delta _{x} \choose \delta _{y}}}$

${\displaystyle {\begin{pmatrix}{\frac {\partial f_{1}}{\partial x}}&{\frac {\partial f_{1}}{\partial y}}\\{\frac {\partial f_{2}}{\partial x}}&{\frac {\partial f_{2}}{\partial y}}\end{pmatrix}}{\delta _{x} \choose \delta _{y}}={-f_{1} \choose -f_{2}}}$is in place . You can choose (−0.5; 1) and (1; −0.5) as starting points. ${\displaystyle (x_{n},y_{n})}$

The easiest way to solve the linear system of equations is with Cramer's rule .

The intersection points are (−0.3686; 0.9953) and (0.9953; −0.3686).

Intersection of two polygons

Intersection of two polygons: window test

If you are looking for points of intersection of two polygons, you can examine each section of one polygon with each section of the other polygon for intersections (see above: intersection of two sections). This simple method is very time-consuming for polygons with many sections. So-called window tests can significantly reduce the computing time. Several sections are combined to form a sub-polygon and the associated window is calculated, which is the minimum axis-parallel rectangle that contains the sub-polygon. Before an intersection point of two partial polygons is laboriously calculated, the associated windows are tested for overlap.

Intersections in space

In 3-dimensional space one speaks of an intersection (common point) of a curve with a surface. In the following considerations (as above) only the transversal sections of a curve with a surface should be treated.

Intersection of a straight line with a plane

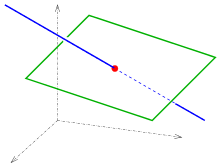
Intersection: straight line - plane

A straight line in space is usually described by a parametric representation and a plane by an equation . Inserting the parametric representation of the straight line into the plane equation results in the linear equation ${\displaystyle (x(t),y(t),z(t))}$ ${\displaystyle ax+by+cz=d}$

${\displaystyle ax(t)+by(t)+cz(t)=d\ ,}$

for the parameter of the intersection . (If the linear equation has no solution, the straight line is parallel to the plane. If the equation is true for all , the straight line is contained in the plane.) ${\displaystyle t_{0}}$ ${\displaystyle (x(t_{0}),y(t_{0}),z(t_{0}))}$ ${\displaystyle t\in \mathbb {R} }$

Intersection of three planes

If a straight line is the intersection of two non-parallel planes and is to be intersected with a third plane , the common point of the 3 planes must be determined. ${\displaystyle \varepsilon _{i}:\ {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\ i=1,2}$ ${\displaystyle \varepsilon _{3}:\ {\vec {n}}_{3}\cdot {\vec {x}}=d_{3}}$

Three planes with linearly independent normal vectors have the point of intersection ${\displaystyle \varepsilon _{i}:\ {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\ i=1,2,3}$ ${\displaystyle {\vec {n}}_{1},{\vec {n}}_{2},{\vec {n}}_{3}}$

${\displaystyle {\vec {p}}_{0}={\frac {d_{1}({\vec {n}}_{2}\times {\vec {n}}_{3})+d_{2}({\vec {n}}_{3}\times {\vec {n}}_{1})+d_{3}({\vec {n}}_{1}\times {\vec {n}}_{2})}{{\vec {n}}_{1}\cdot ({\vec {n}}_{2}\times {\vec {n}}_{3})}}\ .}$

To prove this, convince yourself of observing the rules for a late product . ${\displaystyle {\vec {n}}_{i}\cdot {\vec {p}}_{0}=d_{i},\ i=1,2,3,}$

Intersections of a curve and a surface

Intersection: curve , surface ${\displaystyle (t,t^{2},t^{3})}$ ${\displaystyle x^{4}+y^{4}+z^{4}=1}$

As in the flat case, the following cases lead to generally non-linear systems of equations that can be solved with a 1 or 3-dimensional Newton method:

• parameterized curve and ${\displaystyle K:(x(t),y(t),z(t))}$

parameterized area ${\displaystyle F:(x(u,v),y(u,v),z(u,v))\ ,}$

• parameterized curve and ${\displaystyle K:(x(t),y(t),z(t))}$

implicit area ${\displaystyle F:f(x,y,z)=0\ .}$

Example:

parameterized curve and ${\displaystyle K:(t,t^{2},t^{3})}$

implicit area (see picture) ${\displaystyle F:x^{4}+y^{4}+z^{4}-1=0}$

Equation to solve: ${\displaystyle t^{4}+t^{8}+t^{12}-1=0}$

The intersection points are: (−0.8587; 0.7374; −0.6332), (0.8587; 0.7374; 0.6332).

Note: A straight line can also be contained in a plane. Then there are an infinite number of points in common. A curve can also be partially or completely contained in a surface (see curves on the surface ). In these cases, however, one no longer speaks of an intersection . ${\displaystyle x^{4}+y^{4}+z^{4}-1=0}$

See also

• Intersection (Descriptive Geometry)
• At the intersection
• Positional relationship
• Intersection curve

Individual evidence

1. ↑ Descriptive Geometry for Architects (PDF; 1.5 MB). Script (Uni Darmstadt), pp. 35,73,74
2. ↑ CDKG: Computer-assisted Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 69
3. ↑ CDKG: Computer-assisted Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 79
4. ↑ CDKG: Computer-assisted Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 147.

Web links

Wiktionary: Intersection  - explanations of meanings, word origins, synonyms, translations