Positional relationship

Positional relationship is a term from school mathematics that refers to the relationship between pairs of the geometric objects point, straight line and plane . A typical task in this area is: What is the relationship between a specific straight line and a plane (in 3-dimensional space)? Possible answers are: The straight line intersects the plane at a point or the straight line avoids the plane or the straight line is contained in the plane . The way to the answer depends very much on the description of the straight lines or planes involved (see below). When solving the individual positional problems, linear systems of equations have to be solved again and again . The linear systems of equations are mostly created by equating linear combinations of vectors ("1st component left = 1st component right, ...").

Positional relationships in the (real) plane

Positional relationship straight-straight line: intersect, parallel, identical, skewed

In the plane will

a point described by its coordinates: , ${\ displaystyle (x_ {0}, y_ {0})}$
a straight line is described by a coordinate equation or a parameter representation (see straight line equation ). ${\ displaystyle y = mx + b}$ ${\ displaystyle {\ vec {x}} = {\ vec {p}} + t {\ vec {r}}}$

Point and line

A point is on the line if ${\ displaystyle (x_ {0}, y_ {0})}$ ${\ displaystyle y = mx + b}$

{\ displaystyle y_ {0} = mx_ {0} + b}

applies. Otherwise, the point is not on the straight line.

A point lies on the straight line if the overdetermined system of linear equations ${\ displaystyle (x_ {0}, y_ {0})}$ ${\ displaystyle {\ binom {x} {y}} = {\ binom {p_ {1}} {p_ {2}}} + t {\ binom {r_ {1}} {r_ {2}}}}$

{\ displaystyle x_ {0} = p_ {1} + tr_ {1}}

,

{\ displaystyle y_ {0} = p_ {2} + tr_ {2}}

for a solution. Otherwise, the point is not on the straight line.

{\ displaystyle t}

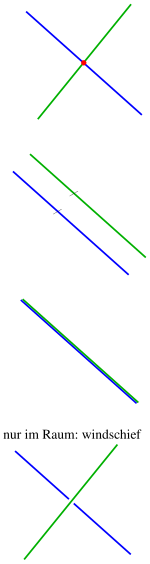
Straight and straight

Two straight lines have an intersection (solution of the linear system of equations) if is. ${\ displaystyle y = m_ {1} x + d_ {1}, \ y = m_ {2} x + d_ {2}}$ ${\ displaystyle m_ {1} \ neq m_ {2}}$

If true, the lines are identical and

{\ displaystyle m_ {1} = m_ {2}, \ d_ {1} = d_ {2}}

if true, the lines are different and parallel .

{\ displaystyle m_ {1} = m_ {2}, \ d_ {1} \ neq d_ {2}}

Two straight lines have an intersection if the equation ${\ displaystyle y = mx + d, \ {\ binom {x} {y}} = {\ binom {p_ {1}} {p_ {2}}} + t {\ binom {r_ {1}} {r_ {2}}}}$

{\ displaystyle p_ {2} + tr_ {2} = m (p_ {1} + tr_ {1}) + d}

for exactly one solution . The intersection has the coordinates .

{\ displaystyle t}

{\ displaystyle t_ {0}}

{\ displaystyle (p_ {1} + t_ {0} r_ {1}, p_ {2} + t_ {0} r_ {2})}

If the equation has no solution, the lines are different and parallel .

If the equation is true for all , the lines are identical .

{\ displaystyle t \ in \ mathbb {R}}

Two straight lines have an intersection, if the system of linear equations ${\ displaystyle {\ binom {x} {y}} = {\ binom {p_ {1}} {p_ {2}}} + t {\ binom {a_ {1}} {a_ {2}}}, \ {\ binom {x} {y}} = {\ binom {q_ {1}} {q_ {2}}} + t {\ binom {b_ {1}} {b_ {2}}}}$

{\ displaystyle p_ {1} + ta_ {1} = q_ {1} + sb_ {1}}

{\ displaystyle p_ {2} + ta_ {2} = q_ {2} + sb_ {2}}

for exactly one solution . The intersection is .

{\ displaystyle s, t}

{\ displaystyle s_ {0}, t_ {0}}

{\ displaystyle (p_ {1} + t_ {0} a_ {1}, p_ {2} + t_ {0} a_ {2})}

If the system of equations has no solution, the lines are different and parallel .

If the system of equations has infinitely many solutions, the two straight lines are identical .

Positional relationships in space

In 3-dimensional space becomes

a point through its coordinates , ${\ displaystyle (x_ {0}, y_ {0}, z_ {0})}$
a straight line through a parametric representation and ${\ displaystyle {\ vec {x}} = {\ vec {p}} + t {\ vec {r}}}$
a plane by a coordinate equation or by a parametric representation ${\ displaystyle ax + by + cz = d}$ ${\ displaystyle {\ vec {x}} = {\ vec {p}} + u {\ vec {e}} + v {\ vec {f}}}$

described (see plane equation ).

For the following studies of positional relationships with layers, it is worth a parameterized given plane by the vector product first coordinate equation set up: . ${\ displaystyle {\ vec {x}} = {\ vec {p}} + u {\ vec {e}} + v {\ vec {f}}}$ ${\ displaystyle ({\ vec {e}} \ times {\ vec {f}}) \ cdot ({\ vec {x}} - {\ vec {p}}) = 0}$

Point and line / plane

Whether a point lies on a straight line or on a plane given by a coordinate equation is checked like the flat cases point - straight line. If the plane is given by a parametric representation, a coordinate equation is first set up for it (see above). ${\ displaystyle (x_ {0}, y_ {0}, z_ {0})}$

Two straight lines

Two straight lines have an intersection point if the overdetermined system of linear equations ${\ displaystyle {\ vec {x}} = {\ vec {p}} + s {\ vec {a}}, \ {\ vec {x}} = {\ vec {q}} + t {\ vec { b}}}$

{\ displaystyle {\ vec {p}} + s {\ vec {a}} = {\ vec {q}} + t {\ vec {b}}}

for exactly one solution . The intersection is then .

{\ displaystyle s, t}

{\ displaystyle s_ {0}, t_ {0}}

{\ displaystyle {\ vec {p}} + s_ {0} {\ vec {a}}}

If no solution exists, the two lines are different and parallel ( are linearly dependent ) or skewed .

{\ displaystyle {\ vec {a}}, {\ vec {b}}}

If there are infinitely many solutions, the lines are identical .

The parallelism of the straight lines can be seen from the fact that the two direction vectors are multiples of each other. ${\ displaystyle {\ vec {a}}, {\ vec {b}}}$

One recognizes skewed direction from the fact that the determinant is. ${\ displaystyle \ det ({\ vec {p}} - {\ vec {q}}, {\ vec {a}}, {\ vec {b}}) \ neq 0}$

Positional relationship straight-plane: intersect, parallel, included

Relationship plane-plane: intersect, parallel, identical

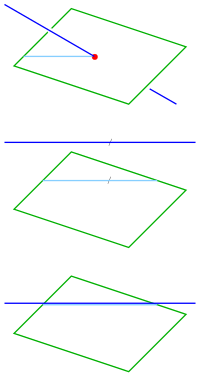
Straight and flat

If the plane is given parameterized, a coordinate equation is first determined.

A straight line intersects the plane if the equation ${\ displaystyle {\ vec {x}} = {\ vec {p}} + t {\ vec {r}}}$ ${\ displaystyle ax + by + cz = d}$

{\ displaystyle a (p_ {1} + tr_ {1}) + b (p_ {2} + tr_ {2}) + c (p_ {3} + tr_ {3}) = d}

for exactly one solution . The intersection is then .

{\ displaystyle t}

{\ displaystyle t_ {0}}

{\ displaystyle {\ vec {p}} + t_ {0} {\ vec {r}}}

If the equation has no or infinitely many solution (s), the straight line is parallel to the plane . (This case can be recognized by the fact that the direction vector of the straight line is perpendicular to the normal vector of the plane, that is, its scalar product is 0.)

{\ displaystyle (a, b, c) ^ {T}}

Two levels

Two planes have exactly one straight line in common ( intersection line ) if the two normal vectors are not multiples of one another (i.e. linearly independent). The straight line of intersection results from the solution of the linear system of equations. ${\ displaystyle a_ {1} x + b_ {1} y + c_ {1} z = d_ {1}, \ a_ {2} x + b_ {2} y + c_ {2} z = d_ {2}}$ ${\ displaystyle (a_ {1}, b_ {1}, c_ {1}), \ (a_ {2}, b_ {2}, c_ {2})}$

If the normal vectors are linearly dependent, the planes are parallel and identical if the two equations are multiples of each other.

Two planes have exactly one straight line in common ( intersection line ), if the linear equation ${\ displaystyle ax + by + cz = d _ {,} \ {\ vec {x}} = {\ vec {p}} + u {\ vec {e}} + v {\ vec {f}}}$

{\ displaystyle a (p_ {1} + ue_ {1} + vf_ {1}) + b (p_ {2} + ue_ {2} + vf_ {2}) + c (p_ {3} + ue_ {3} + vf_ {3}) = d}

is resolvable in after or . If the equation is solvable for and , then a parametric representation of the intersection line is freely selectable .

{\ displaystyle u, v}

{\ displaystyle u}

{\ displaystyle v}

{\ displaystyle u}

{\ displaystyle u = u (v)}

{\ displaystyle v}

{\ displaystyle {\ vec {x}} = {\ vec {p}} + u (v) {\ vec {e}} + v {\ vec {f}}}

If the equation is neither solvable for nor for , both parameters are not included in the equation. In this case the planes are parallel and different if the equation contains a contradiction. (This case can be recognized by the fact that the normal vector of the first plane is perpendicular to both direction vectors of the second plane, i.e. the corresponding scalar products are 0.)

{\ displaystyle u}

{\ displaystyle v}

{\ displaystyle (a, b, c) ^ {T}}

{\ displaystyle {\ vec {e}}, {\ vec {f}}}

If both planes are parameterized, a coordinate equation is calculated for one of the two planes and the above procedure is used.

Generalizations

Since the position investigations only involve multiplication and addition, the above considerations can also be transferred to levels / spaces using any number fields (rational numbers, complex numbers, ...).
In some books, circles and spheres are added to the objects (point, straight line, plane). In this case one also has to solve quadratic equations.
One can also examine positional relationships in higher dimensional spaces for points, lines, planes, ..., subspaces.

literature

Mathematics 2.2 (Upper School Hesse), Cornelsen-Verlag, 2010, ISBN 978-3-464-57455-3 , p. 118

Web links