In mathematics, a quadric (from the Latin quadra square) is the set of solutions to a quadratic equation of several unknowns. In two dimensions, a quadric usually forms a curve in the plane , which is then a conic section . In three dimensions, a quadric generally describes an area in space , which is also called a second-order area or a square area . In general, a quadric is an algebraic variety , i.e. a special hypersurface in a finite-dimensional real coordinate space . Each quadric can be transformed to one of three possible normal forms by means of a major axis transformation. In this way, quadrics can be classified into several basic types.
Quadrics are particularly studied in analytical and projective geometry . Applications for quadrics in technology and the natural sciences can be found in geodesy ( reference ellipsoid ), architecture ( supporting structure ) or optics ( parabolic mirrors ).
definition
A quadric is a set of points in the -dimensional real coordinate space of the form


-
 ,
,
in which

is a quadratic polynomial in variables . At least one of the polynomial coefficients must be non-zero. In addition, it can be assumed without restriction that applies to all . A quadric is the set of zeros of a quadratic polynomial of several variables or the set of solutions of a quadratic equation with several unknowns.




Examples
For example, describes the set of points

an ellipse in the plane. The amount of points

describes a single-shell hyperboloid in three-dimensional space.
properties
Matrix display
In compact matrix notation , a quadric can be used as a set of vectors

are described, where a symmetrical matrix and and column vectors are of corresponding length. With the help of the extended display matrix




and a correspondingly expanded vector can also make a quadric compact by the set


are represented in homogeneous coordinates .
Types
There are three basic types of quadrics. The decision of what type a given quadric is can be made based on the ranks of the matrices , and :



-
Conical type :

-
Center square :

-
Parabolic type :

A quadric is called degenerate , if

applies. While non-degenerate quadrics form curved hypersurfaces in all directions, degenerate quadrics have linear structures in some directions or are otherwise degenerate.
Transformations
Quadrics can be transformed through similarity maps without changing their type. If it is a regular matrix , the linear transformation gives a new quadric in the coordinates , that of the equation




enough. A parallel shift by a vector also gives a new quadric, which is the equation



met with the identity matrix . In particular, the rank of the matrices and such affinities do not change.



If so, both methods can be combined using and :





Since the matrix is symmetric, it is orthogonally diagonalizable, that is, there is an orthogonal matrix such that is a diagonal matrix. With this the quadric can through the condition




be expressed. So there are no longer any mixed-quadratic or linear terms. The center of the quadric is thus included .

Normal forms
Each quadric can be transformed to one of the following normal forms using a major axis transformation. For this purpose, an orthogonal matrix , for example a rotation or reflection matrix , is first selected in such a way that a diagonal matrix results which contains the eigenvalues of in descending order. In the second step, the transformed quadric is shifted by a vector in such a way that the linear terms and the constant term also largely disappear. Finally, the quadric is normalized in such a way that the constant term, if it is not zero, becomes one. This results in the following three normal forms:




- Conical type: with


- Center square: with


- Parabolic type: with


In addition, there is the special case
- Empty set: with


In all cases the coefficients are . The key figures and result from the signature of the matrix .




classification
Quadrics in one dimension
In one dimension, a quadric is the set of solutions to a quadratic equation with an unknown, i.e. a set of points of the form
-
 .
.
The following two cases can be distinguished by shifting ( square addition ) and normalization:
| Non-degenerate quadrics
|
Degenerate quadrics
|
Two solutions

|

|
A solution

|

|
In the remaining case , the solution set is the empty set. In all cases it is .


Quadrics in the plane
In the plane, a quadric is the set of solutions to a quadratic equation with two unknowns, i.e. a set of points of the form
-
 .
.
Except for degenerate cases, these are conic sections , with degenerate conic sections, in which the cone tip is contained in the cutting plane, and non-degenerate conic sections are distinguished. The general equation of a quadric can be transformed to one of the following normal forms using principal axis transformation:
| Non-degenerate quadrics
|
Degenerate quadrics
|
ellipse

|

|
Two intersecting straight lines

|

|
hyperbole

|

|
Two parallel straight lines

|
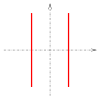
|
parabola

|

|
A straight

|

|
|
|
|
One point

|

|
In the two remaining cases and , the solution set is the empty set. In all cases are .



Quadrics in space
In three-dimensional space, a quadric is the solution set of a quadratic equation with three unknowns, i.e. a point set of the form
-
 .
.
In space, the variety of quadrics is significantly greater than in the plane. There are degenerate and non-degenerate quadrics here as well. The degenerate quadrics also include simply curved surfaces such as cylinders and cones. Similar to two dimensions, the general equation of a quadric can be transformed to one of the following normal forms:
| Non-degenerate quadrics
|
Degenerate quadrics (curved surfaces)
|
Degenerate quadrics (levels, etc.)
|
Ellipsoid

|

|
Elliptical cone

|
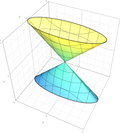
|
Two intersecting planes

|
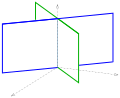
|
Single-shell hyperboloid

|

|
Elliptical cylinder

|

|
Two parallel planes

|
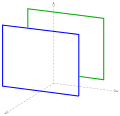
|
Double-shell hyperboloid

|

|
Hyperbolic cylinder

|

|
A level

|

|
Elliptical paraboloid

|

|
Parabolic cylinder

|

|
A straight

|

|
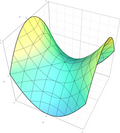
Hyperbolic paraboloid

|
|
|
|
One point

|

|
In the three remaining cases , and the empty set is the result of the solution set. In all cases are .




For (or is obtained in the case of the two-sheeted hyperboloid) in the following cases, surfaces of revolution , also called rotational quadric be referred to: ellipsoid , single- and double-shelled hyperboloid of revolution , paraboloid of revolution , a circular cone , and a circular cylinder . Ruled surfaces , i.e. surfaces that are generated by a single -parameter family of straight lines , are cones, elliptical and parabolic cylinders, planes, single-shell hyperboloid and hyperbolic paraboloid. The latter three surfaces are even generated by two sets of straight lines and are the only possible double-curved ruled surfaces in space.


Projective Quadrics
The diversity of the quadrics is considerably reduced if both the affine space in which a quadric is defined and the quadric itself are projectively closed . The projective extensions of ellipses, hyperbolas and parabolas are all projectively equivalent to one another, that is, there is a projective collineation that maps one curve onto the other (see projective conic section ).
In three-dimensional space, the following quadrics are equivalent:
- Ellipsoid, double-shell hyperboloid and elliptical paraboloid,
- single-shell hyperboloid and hyperbolic paraboloid,
- elliptical, hyperbolic, parabolic cylinder and cone.
Generalizations
More generally, quadrics can also be viewed in vector spaces over any body , i.e. also over the body of complex numbers or even over finite bodies .
Individual evidence
-
^ A b Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth Stachel : Mathematics . 2nd Edition. Spektrum Akademischer Verlag, 2011, ISBN 3-8274-2347-3 , pp. 719 .
-
^ Kurt Meyberg, Peter Vachenauer: Higher Mathematics 1 . 6th edition. Springer, 2003, ISBN 978-3-540-41850-4 , pp. 345 .
-
↑ Hanfried Lenz : Lectures on projective geometry. Academic publishing company Geest & Portig, Leipzig 1965, p. 155.
literature
- Ilja Nikolajewitsch Bronstein, Konstantin A. Semendjajew: Pocket book of mathematics. Teubner-Verlag, Leipzig 1983, ISBN 3-87144-492-8 , p. 283.
- Klemens Burg, Herbert Haf, Friedrich Wille: Higher Mathematics for Engineers. Volume II, Teubner-Verlag, Stuttgart, ISBN 3-519-22956-0 , p. 341.
-
dtv atlas on mathematics. Volume 1, Deutscher Taschenbuch-Verlag, ISBN 3-423-03007-0 , pp. 200-203.
- Kurt Meyberg, Peter Vachenauer: Höhere Mathematik 1. Springer-Verlag, Berlin 1995, ISBN 3-540-59188-5 , p. 343.
Web links








































































































