Homogeneous coordinates
In projective geometry , homogeneous coordinates are used to represent points in a projective space using numerical values and thus to make geometrical problems accessible for computational processing. Compared to the (inhomogeneous) coordinates normally used , which uniquely identify each point, homogeneous coordinates have the property that they are not clearly determined for a given point. The advantage of homogeneous coordinates lies in the uniform representation of the elements of a projective space, in which remote elements no longer play a special role. In addition, by using homogeneous coordinates, all collineations , and thus also parallel displacements , can be uniformly described by linear images and thus by matrices . For this reason, homogeneous coordinates in three-dimensional space play an important role in computer graphics .
Projective coordinate systems
Homogeneous coordinates
Homogeneous coordinates can best be understood using the example of the real projective plane . The projective straight line and higher-dimensional projective spaces are provided with coordinates analogously. In the homogeneous model corresponds to the real projective plane
- a point of the projective plane of a straight line through the origin in three-dimensional space and
- a straight line of the projective plane of an original plane in three-dimensional space.
A point then lies on a straight line if the straight line through the origin belonging to the point lies in the plane of the origin belonging to the straight line (see figure). A point of the projective plane can thus be described by any point on the associated straight line through the origin. Then you write
and calls homogeneous coordinates of the point . Obviously,
for each number . A straight line of the projective plane is then described by a (homogeneous) plane equation . In this model, it is easy to convince oneself of the basic incidence properties of a projective plane:
- For every two different points there is exactly one connecting line that contains both points.
- Every two different straight lines have exactly one point of intersection.
Inhomogeneous coordinates
In the inhomogeneous model of the real projective plane, one starts from the visual plane and supplements the point set with far points in such a way that every two straight lines, i.e. also parallel straight lines, intersect at exactly one point.
After the introduction of Cartesian coordinates, the far point is usually added to every straight line with the slope . The straight lines (parallels to the y-axis) receive the far point (see picture). Since two far points must be connected by a straight line, all far points are combined to form a far straight line . It is easy to check that the new incidence structure (expanded view level) fulfills the essential properties of a projective level:
- Every two points have exactly one connecting line.
- Every two straight lines have exactly one point of intersection.
Isomorphism
In order to show that the homogeneous and inhomogeneous model of the real projective plane are isomorphous, the inhomogeneous model is so embedded in the three-dimensional space, that the points of view plane of the equation satisfy: . The point of the homogeneous model is thus assigned to the point of the inhomogeneous model . A point is mapped to the point whose homogeneous coordinates satisfy the equation . So one can assign the straight line through origin common to all planes of origin to the far point common to all inhomogeneous straight lines (see picture).
The great advantage of homogeneous coordinates compared to the clearer inhomogeneous coordinates lies in the homogeneous representation of the points and straight lines. Far points and long distance lines no longer play a special role and all collineations, including translations, can be uniformly described by linear images (matrices). The latter plays a particularly important role in computer graphics .
Summary:
Reversal:
- if
- if
Assignment of the straight lines:
The embedding is not presented uniformly in the literature. The homogeneous coordinates can also be designated with or the line in the distance can satisfy the equation .
general definition
Every point in a -dimensional projective space can be described by coordinates. The projective space above the body is defined as the factor space
of the coordinate space without the zero vector with respect to the equivalence relation
- .
The homogeneous coordinates of a point in projective space are then , where any element is of the corresponding equivalence class . Homogeneous coordinates are often due to
- or
noted, whereby the colons should indicate that the representation is only unique up to multiplication with a constant.
Projective transformations
In two-dimensional space
In the following, examples and finally all affine mappings are initially continued in the inhomogeneous model for projectivities and then described in the homogeneous model by matrices. However, it must be ensured that the respective matrices (in the homogeneous model) are not clearly determined. Because not only the identity matrix , but every multiple (scaling matrix im ) leaves every straight line through the origin (projective point) invariant. The matrix of a projectivity can therefore be multiplied by any scaling matrix without the associated projectivity changing.
| a): | |
| b): | |
| c): |
The continuations of the affinities only provide those collineations that leave the distance line fixed as a whole. The associated matrices in the homogeneous model are characterized by the fact that they have a 0 in the third position in the first two columns. So not all matrices appear yet. But the following applies:
- Every regular 3 × 3 matrix (determinant not 0) induces a collineation of the projective plane, which is called projectivity . The set of projectivities form the group ( projective linear group ).
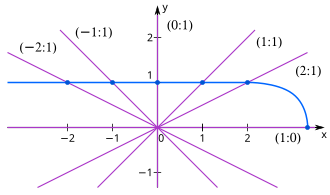
E.g .: The matrix induces a projectivity which, in the inhomogeneous model, swaps the distance line with the y-axis and the point with the point . (The points are fixed points.) So it is not a continuation of an affinity.
If one wants to represent any projectivity in the inhomogeneous model, this is only possible with broken linear expressions. This shows the strength of the homogeneous model. It gets by with linear expressions.
In three-dimensional space
Similar to the plane case, homogeneous coordinates can also be introduced in 3-dimensional projective space. There are then 4 homogeneous coordinates and the mapping matrices of the projectivities are 4 × 4 matrices. In computer graphics, not only transformations of space in homogeneous coordinates are represented by 4 × 4 matrices, but also projections of space onto a plane (see graphics pipeline ). Since the dimension is reduced in such projections (from 3 to 2), the associated matrices have the determinant 0. Here are two examples of projection matrices:
The first matrix describes the central projection from the eye point onto the xy plane. The second matrix effects an orthogonal projection onto the xy plane.
| Central projection : | = | |||
| Orthogonal projection : | = |
Applications
Homogeneous coordinates are used within geometry
- Examine conic sections (see projective conic sections ),
- To investigate collineations of projective lines, planes and spaces ( projective linear group ).
In computer graphics , homogeneous coordinates are used to
- Perform transformations of objects,
- introduce and investigate rational Bezier and B-spline curves and surfaces.
In robotics , consecutive axes can be described by linking their associated homogeneous matrices. The Denavit-Hartenberg transformation is used as the standard procedure for this .
literature
- Albrecht Beutelspacher , Ute Rosenbaum: Projective geometry. 2nd Edition. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X , p. 63.
- G. Farin: Curves and Surfaces for CAGD , Academic Press, 1990, ISBN 0-12-249051-7 , p. 217
- CE Springer: Geometry and Analysis of Projective Spaces . San Francisco and London, 1964.
- Frank Klawonn: Basic course computer graphics with Java. Understand the basics and easily implement them with Java 3D. 3. Edition. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1223-0 .
Web links
- W. Globke: Coordinates, Transformations and Robots , University of Karlsruhe, p. 20.
- S. Krömker: Computergraphik I , University of Heidelberg, p. 29.
- M. Pester: Mathematical Foundations of Computer Geometry, Chemnitz University, p. 7.
Individual evidence
- ↑ Ina Kersten: Analytical Geometry and Linear Algebra . tape 2 . Universitätsverlag Göttingen, 2006, ISBN 978-3-938616-44-4 , p. 85 .
- ↑ Hoschek, Lasser: Fundamentals of geometrical data processing , Teubner 1989, ISBN 3-519-02962-6 , p. 143.
- ^ G. Farin: Curves and Surfaces for CAGD , Academic Press, 1990, ISBN 0-12-249051-7 , p. 231.


















































![P = \ left [x_ {0} \ colon x_ {1} \ colon \ ldots \ colon x_ {n} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3539335a1f49a342d3045b9ddfee0d1859b43333)




















