Graphics pipeline
A computer graphics pipeline , also called rendering pipeline or simply graphics pipeline , is a model concept in computer graphics that describes the steps a graphics system has to carry out to render , i.e. to display a 3D scene on a screen. Since these steps depend on the software and hardware as well as on the desired display properties, there is no generally valid graphics pipeline. Graphics APIs such as Direct3D or OpenGL are usually used to control graphics pipelines , which abstract the underlying hardware and relieve the programmer of many tasks.
The representation of three-dimensional worlds on the computer is widespread today and is part of very many computer games. The so-called rendering creates graphics from abstract data.
The graphics pipeline model is typically used in real-time rendering. Here, most of the steps in the pipeline are often implemented in hardware , which enables special optimizations. The term “pipeline” is used in a similar sense to the pipeline for processors : The individual steps of the pipeline run in parallel, but are blocked until the slowest step has been completed.
construction
A graphics pipeline can be broken down into three major steps: application, geometry, and rasterization.
application
The application step is carried out by the software, so it cannot be broken down into pipelined individual steps. However, it is possible to parallelize it on multi-core processors or multi-processor systems . In the application step, changes are made to the scene, such as are necessary due to user interaction using input devices or during an animation . The new scene with all of its primitives - mostly triangles, lines and points - is then passed on to the next step in the pipeline.
Examples of tasks that are typically taken over by the application step are collision detection , animation, morphing and data management. The latter include, for example, acceleration techniques using spatial subdivision schemes ( quadtree , octree ) with which the data currently held in the memory are optimized. The “world” and its textures of today's computer game are much larger than could be loaded into the available RAM or graphics memory all at once.
geometry
The geometry step that for the majority of operations with polygons and their vertices ( vertices is responsible), can be divided into the following five tasks. How these tasks are organized as actual pipeline steps running in parallel depends on the specific implementation.
Definitions
A vertex (plural: vertices ) is a point in the world. These points are used to connect the surfaces. In special cases point clouds are drawn directly , but this is still the exception.
A triangle (English: Triangle ) is the most common geometric primitive in computer graphics. It is defined by its three corners and a normal vector - the latter is used to indicate the front of the triangle and is a vector that is perpendicular to the surface. Such a triangle can be given a color or a texture .
The world coordinate system
The world coordinate system is the coordinate system in which the virtual world is created. This should meet some conditions so that the following mathematics can be easily applied: It must be a right-angled Cartesian coordinate system in which all axes are scaled equally. How the unit of the coordinate system is determined, however, is left to the developer. So whether the unit vector of the system should actually correspond to a meter or an Angstrom depends on the application. The graphics library to be used can specify whether a right-handed or left-handed coordinate system is to be used.
- Example: If we want to develop a flight simulator, we can choose the world coordinate system so that the origin is in the center of the earth and set the unit to be one meter. In addition, we define - so that the relation to reality is easier - that the X-axis should intersect the equator on the prime meridian and the Z-axis runs through the poles. In a right system, the Y-axis runs through the 90 ° east meridian (somewhere in the Indian Ocean). Now we have a coordinate system that describes every point on earth in Cartesian coordinates. In this coordinate system we are now modeling the main features of our world, i.e. mountains, valleys and waters.
- Note: Outside of computer geometry, geographic coordinates are used for the earth, i.e. degrees of longitude and latitude , as well as heights above sea level. The approximate conversion - if one disregards the fact that the earth is not an exact sphere - is simple:
- with R = earth radius [6.378.137m], lat = latitude, long = longitude, hasl = height above sea level.
- All of the following examples apply in a legal system. For a left system, signs may have to be swapped.
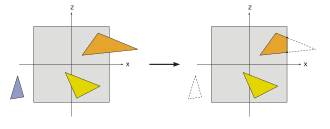
The objects specified in the scene (houses, trees, cars) are often specified in their own object coordinate system (also model coordinate system or local coordinate system ) for reasons of simpler modeling . In order to assign these objects coordinates in the world coordinate system or global coordinate system of the entire scene, the object coordinates are transformed by means of translation, rotation or scaling. This is done by multiplying the corresponding transformation matrices . In addition, several differently transformed copies can be formed from an object, for example a forest from a tree; this technique is called instancing .
- To place a model of an airplane in the world, we first determine four matrices. Since we are working in three-dimensional space, the homogeneous matrices that we need for our calculation are four-dimensional. First we need three rotation matrices, namely one for each of the three aircraft axes (vertical axis, transverse axis, longitudinal axis).
- Around the X axis (usually defined as the longitudinal axis in the object coordinate system)
- Around the Y-axis (usually defined as the transverse axis in the object coordinate system)
- Around the Z axis (usually defined as the vertical axis in the object coordinate system)
- We also apply a translation matrix, which shifts the plane to the desired point in our world: .
- Note: The above matrices are transposed to those in the article Rotary matrix . The explanation is in the following section.
Now we could calculate the position of the aircraft's vertices in world coordinates by multiplying each point in turn by these four matrices. Since the multiplication of a matrix by a vector is quite complex, one usually takes a different approach and first multiplies the four matrices together. The multiplication of two matrices is even more expensive, but only has to be carried out once for the entire object. The multiplications and are equivalent. Then the resulting matrix could be applied to the points. In practice, however, the multiplication by the points is still not used, but the camera matrices - see below - are determined first.
- For our example from above, however, the translation has to be determined a little differently, since the meaning of "above" - except at the North Pole - does not match the positive Z-axis and therefore the model must also be rotated around the center of the earth. The first step moves the origin of the model to the correct height above the surface of the earth, then it is rotated by length and width.
The order in which the matrices are applied is important because matrix multiplication is not commutative . This also applies to the three rotations, as you can see with an example: The point (1, 0, 0) lies on the X-axis if you first move it by 90 ° around the X- and then around If the Y-axis rotates, it ends up on the Z-axis (the rotation around the X-axis has no effect on a point on the axis). If you rotate first around the Y and then around the X axis, the resulting point is on the Y axis. The order itself is arbitrary, as long as it is always the same. The order with x, then y, then z (roll, pitch, heading) is often the most intuitive, because the rotation causes u. a. that the compass direction coincides with the direction of the "nose".
There are also two conventions for defining these matrices, depending on whether you want to work with column vectors or row vectors. Different graphics libraries have different preferences here. For example, OpenGL prefers column vectors, DirectX row vectors. From the decision it follows from which side the point vectors are multiplied to the transformation matrices. For column vectors multiplication from right, so , where v out and v in representing × 1 column vectors. 4 The matrices are also concatenated from right to left, for example when rotating first and then shifting. The opposite is true for row vectors. The multiplication now takes place from the left as with 1 × 4 vectors and the concatenation reads if it is also rotated first and then shifted. The matrices shown above apply to the second case, those for column vectors result as transpose of them. The rule applies , which means for multiplication with vectors that the order of multiplication can be exchanged by transposing.
The interesting thing about this matrix chaining is that a new coordinate system is defined by each such transformation. That can be continued at will. For example, the propeller of the aircraft can be available as a separate model, which is then placed on the aircraft nose by a translation. This translation only needs to describe the shift from the model coordinate system to the propeller coordinate system. To draw the entire aircraft, the transformation matrix for the aircraft is first determined, the points are transformed and then the translation to the propeller model is then multiplied onto the matrix of the aircraft and then the propeller points are transformed.
The matrix calculated in this way is also called the world matrix (English: world transformation ). It must be determined for every object in the world before it is displayed. The application can influence changes here, e.g. change the position of our aircraft according to the speed.
Camera transformation
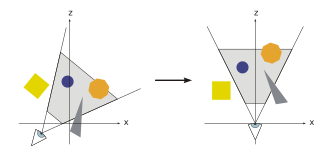
In addition to the objects, the scene also defines a virtual camera or a viewer who indicates the position and viewing direction from which the scene is to be rendered. In order to simplify later projection and clipping , the scene is transformed so that the camera is at the origin, looking along the Z axis. The resulting coordinate system is called the camera coordinate system and the transformation is called the camera transformation (English view transformation ).
- The view matrix is usually determined from the camera position, the target point (where the camera is looking) and an up vector (“up” from the viewer's point of view). First three auxiliary vectors are needed:
- zaxis = normal (cameraPosition - cameraTarget)
- xaxis = normal (cross (cameraUpVector, zaxis))
- yaxis = cross (zaxis, xaxis)
- With normal (v) = normalization of the vector v; cross (v1, v2) = cross product of v1 and v2.
- Finally the matrix:
- With dot (v1, v2) = scalar product of v1 and v2.
projection
The projection step transforms the visual volume into a cube with the corner point coordinates (-1, -1, -1) and (1, 1, 1); other target volumes are occasionally used. This step is called projection, although it transforms one volume into another volume, since the resulting Z coordinates are not stored in the image, but are only used for Z buffering in the later rasterization step . In a perspective illustration one is central projection used. To limit the number of objects shown, two additional clipping planes are used; the visual volume is thus a truncated pyramid ( frustum ). The parallel or orthogonal projection is used, for example, for technical representations, because it has the advantage that all parallels in the object space are also parallel in the image space and areas and volumes are of the same size regardless of the distance to the viewer. Maps, for example, also use an orthogonal projection (so-called orthophoto ), but oblique images of a landscape are not to be used because - although technically naturally representable - they appear so distorted to us that we cannot do anything with them.
- The formula for calculating a perspective mapping matrix is:
- With h = cot (fieldOfView / 2.0) (opening angle of the camera); w = h / aspectRatio (aspect ratio of the target image); near = smallest distance that should be visible; far = furthest distance that should be visible.
The reasons why the smallest and the largest distance have to be specified here are, on the one hand, that this distance is divided in order to achieve the size scaling (objects further away are smaller than near objects in a perspective illustration) and, on the other hand, that so that the Z values are scaled to the range 0..1, with which the Z buffer is then filled. This often only has a resolution of 16 bits, which is why the near and far values should be chosen carefully. Too great a difference between the near and far value leads to so-called Z-fighting because of the low resolution of the Z-buffer . The formula also shows that the near value cannot be 0 because this point is the focal point of the projection. There is no picture at this point.
- For the sake of completeness, the formula for the parallel projection (orthogonal projection):
- With w = width of the target cube (dimension in units of the world coordinate system); h = w / aspectRatio (aspect ratio of the target image); near = smallest distance that should be visible; far = furthest distance that should be visible.
For reasons of efficiency, the camera matrix and the projection matrix are usually combined in a transformation matrix so that the camera coordinate system is ignored. The resulting matrix is usually the same for a single image, while the world matrix looks different for each object. In practice, view and projection are therefore precalculated so that only the world matrix has to be adjusted during the display. However, other, more complex transformations such as vertex blending are possible. Freely programmable geometry shaders that change the geometry can also be executed. In the actual rendering step, the world matrix * camera matrix * projection matrix is calculated and this is then finally applied to each individual point. This transfers the points of all objects directly to the screen coordinate system (at least almost, the value ranges of the axes are still −1..1 for the visible area, see section "Window-Viewport-Transformation").
lighting
Often a scene contains light sources placed in different positions to make the lighting of the objects appear more realistic. In this case, a gain factor for the texture is calculated for each vertex based on the light sources and the material properties belonging to the corresponding triangle . In the later rasterization step, the corner point values of a triangle are interpolated over its area . General lighting ( ambient light ) is applied to all surfaces. It is the diffuse and therefore direction-independent brightness of the scene. The sun is a directed light source that can be assumed to be infinitely far away. The lighting that the sun causes on a surface is determined by forming the scalar product of the directional vector of the sun and the normal vector of the surface. If the value is negative, the surface is facing the sun.
Clipping
Only the primitives that are within the visual volume actually have to be rasterized. Primitives that are completely outside of the visual volume are discarded; this is called frustum culling . Further culling methods such as backface culling , which reduce the number of primitives to be considered, can theoretically be carried out in any step of the graphics pipeline. Primitives that are only partially inside the cube must be clipped against the cube. The advantage of the previous projection step is that the clipping always takes place against the same cube. Only the primitives - possibly clipped - that are located within the visual volume are passed on to the next step.
Window viewport transformation
In order to output the image to any target area (viewport) on the screen, another transformation, the window viewport transformation , must be applied. This is a shift followed by a scaling. The resulting coordinates are the device coordinates of the output device. The viewport contains 6 values: height and width of the window in pixels, the upper left corner of the window in window coordinates (mostly 0, 0) and the minimum and maximum values for Z (mostly 0 and 1).
- So is
- With vp = viewport; v = point after projection
On modern hardware, most of the geometry calculation steps are performed in the vertex shader . In principle, this is freely programmable, but generally takes on at least the transformation of the points and the lighting calculation. For the DirectX programming interface , from version 10, the use of a user-defined vertex shader is inevitable, while older versions still provided a standard shader.
Rasterization
In the rasterization step, all primitives are rasterized , i.e. discrete fragments are created from continuous surfaces .
In this stage of the graphics pipeline, the raster points are also called fragments to make them easier to distinguish. H. each fragment corresponds to a pixel in the frame buffer and this corresponds to a pixel of the screen.
These can then be colored (if necessary illuminated). Furthermore, in the case of overlapping polygons, it is necessary to determine the visible one, i.e. the one closer to the viewer. A Z-buffer is usually used for this so-called masking calculation . The color of a fragment depends on the lighting, texture and other material properties of the visible primitive and is often interpolated using the triangle vertex points. Where available, a fragment shader is run through in the rasterization step for each fragment of the object. If a fragment is visible, it can now be mixed with existing color values in the image, if transparencies are simulated or multi-sampling is used. In this step, one or more fragments become a pixel.
Double buffering takes place so that the user does not see the gradual rasterization of the primitives . The rasterization takes place in a special memory area. As soon as the image has been completely rasterized, it is copied all at once into the visible area of the image memory .
Inverse
All matrices used are regular and can therefore be inverted. Since the multiplication of two regular matrices creates a regular matrix again, the entire transformation matrix can also be inverted. The inverse is required in order to calculate world coordinates from screen coordinates - for example to infer the clicked object from the mouse pointer position. But since the screen and the mouse only have two dimensions, the third is unknown. A ray is therefore projected into the world at the cursor position and then the intersection of this ray with the polygons in the world is determined.
Shader
Classic graphics cards were still relatively closely based on the graphics pipeline in terms of their internal structure. With increasing demands on the GPU , restrictions were gradually lifted in order to create more flexibility. Modern graphics cards use a freely programmable shader-controlled pipeline , which allows direct intervention in individual processing steps. In order to relieve the main processor, additional processing steps were introduced within the pipeline, which previously only ran on the CPU .
The most important shader units are pixel shaders , vertex shaders and geometry shaders . The unified shader was introduced in order to make optimal use of all units . This means that there is only one large, uniform pool of shader units. Depending on requirements, the pool is divided into different groups of shaders. A strict separation between the shader types is therefore no longer useful. In the meantime, it is also possible to use a so-called compute shader to perform any calculations on the GPU apart from the display of a graphic. The advantage is that they run in parallel, but there are limitations. These universal calculations are also called GPGPU .
literature
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. AK Peters, Natick MA 2002, ISBN 1-56881-182-9 .
- Michael Bender, Manfred Brill: Computer graphics: an application-oriented textbook. Hanser, Munich 2006, ISBN 3-446-40434-1 .
- Martin Fischer: Pixel Factory. How graphics chips conjure up game worlds on the screen . In: c't magazine for computer technology . Heise Zeitschriften Verlag, July 4, 2011, p. 180 .
Individual evidence
- ↑ Tomas Akenine-Möller, Eric Haines: Real-Time Rendering . P. 11.
- ↑ K. Nipp, D. Stoffer; Linear algebra ; v / d / f university publisher of the ETH Zurich; Zurich 1998, ISBN 3-7281-2649-7 .