Symmetrical matrix

Symmetry pattern of a symmetric (5 × 5) matrix

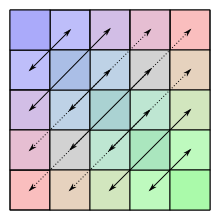
In mathematics, a symmetrical matrix is a square matrix whose entries are mirror-symmetrical with respect to the main diagonal . A symmetrical matrix therefore corresponds to its transposed matrix .

The sum of two symmetric matrices and every scalar multiple of a symmetric matrix is ​​again symmetric. The set of symmetrical matrices of fixed size therefore forms a subspace of the associated matrix space . Every square matrix can be clearly written as the sum of a symmetrical and a skew-symmetrical matrix . The product of two symmetric matrices is symmetric if and only if the two matrices commute . The product of any matrix with its transpose results in a symmetrical matrix.

Symmetric matrices with real entries have a number of other special properties. A real symmetric matrix is ​​always self-adjoint , it has only real eigenvalues and it is always orthogonally diagonalizable . In general, these properties do not apply to complex symmetric matrices; the corresponding counterparts there are Hermitian matrices . An important class of real symmetric matrices are positive definite matrices in which all eigenvalues ​​are positive.

In linear algebra , symmetric matrices are used to describe symmetric bilinear forms . The representation matrix of a self-adjoint mapping with respect to an orthonormal basis is also always symmetrical. Linear systems of equations with a symmetrical coefficient matrix can be solved efficiently and numerically stable . Furthermore, symmetrical matrices are used in orthogonal projections and in the polar decomposition of matrices.

Symmetric matrices have applications in geometry , analysis , graph theory and stochastics, among others .

definition

A square matrix over a body is called symmetric if for its entries ${\displaystyle A=(a_{ij})\in K^{n\times n}}$ ${\displaystyle K}$

${\displaystyle a_{ij}=a_{ji}}$

for applies. A symmetrical matrix is ​​therefore mirror-symmetrical with respect to its main diagonal , that is, it applies ${\displaystyle i,j=1,\ldots ,n}$

${\displaystyle A=A^{T}}$,

where denotes the transposed matrix . ${\displaystyle A^{T}}$

Examples

Examples of symmetric matrices with real entries are

${\displaystyle {\begin{pmatrix}2\end{pmatrix}},\quad {\begin{pmatrix}1&5\\5&7\end{pmatrix}},\quad {\begin{pmatrix}1&1\\1&0\end{pmatrix}},\quad {\begin{pmatrix}1&3&0\\3&2&6\\0&6&5\end{pmatrix}}}$.

Generally symmetrical matrices have the size , and structure ${\displaystyle 2\times 2}$ ${\displaystyle 3\times 3}$ ${\displaystyle 4\times 4}$

${\displaystyle {\begin{pmatrix}a&b\\b&c\end{pmatrix}},\quad {\begin{pmatrix}a&b&c\\b&d&e\\c&e&f\end{pmatrix}},\quad {\begin{pmatrix}a&b&c&d\\b&e&f&g\\c&f&h&i\\d&g&i&j\end{pmatrix}}}$.

Classes of symmetric matrices of any size are among others

• Diagonal matrices , especially standard matrices ,
• constant square matrices, for example square zero matrices and single matrices ,
• Hankel matrices in which all opposing diagonals have constant entries, e.g. Hilbert matrices ,
• bisymmetrical matrices that are symmetrical with respect to both the main diagonal and the opposite diagonal.

properties

Entries

With a symmetrical matrix, only the entries on and below the diagonal need to be saved

Due to the symmetry, a symmetrical matrix is clearly characterized by its diagonal entries and the entries below (or above) the diagonals. A symmetric matrix therefore has at most ${\displaystyle A\in K^{n\times n}}$ ${\displaystyle n}$ ${\displaystyle {\tfrac {n(n-1)}{2}}}$

${\displaystyle n+{\frac {n(n-1)}{2}}={\frac {n(n+1)}{2}}}$

different entries. In comparison, a non-symmetrical matrix can have up to different entries, i.e. almost twice as many for large matrices. There are therefore special storage formats for storing symmetrical matrices in the computer that take advantage of this symmetry. ${\displaystyle (n\times n)}$ ${\displaystyle n^{2}}$

total

The sum of two symmetrical matrices is always symmetrical again, because ${\displaystyle A+B}$ ${\displaystyle A,B\in K^{n\times n}}$

${\displaystyle (A+B)^{T}=A^{T}+B^{T}=A+B}$.

Likewise, the product of a symmetrical matrix with a scalar is again symmetrical. Since the zero matrix is ​​also symmetric, the set of symmetric matrices forms a subspace ${\displaystyle cA}$ ${\displaystyle c\in K}$ ${\displaystyle n\times n}$

${\displaystyle \operatorname {Symm} _{n}=\{A\in K^{n\times n}\mid A^{T}=A\}}$

of the die space . This subspace has the dimension , wherein the standard dies , and , in a base form. ${\displaystyle K^{n\times n}}$ ${\displaystyle {\tfrac {n^{2}+n}{2}}}$ ${\displaystyle E_{ii}}$ ${\displaystyle 1\leq i\leq n}$ ${\displaystyle E_{ij}+E_{ji}}$ ${\displaystyle 1\leq i<j\leq n}$

Disassembly

If the characteristic of the body is not equal to 2, any square matrix can be written uniquely as the sum of a symmetric matrix and a skew-symmetric matrix by ${\displaystyle K}$ ${\displaystyle M\in K^{n\times n}}$ ${\displaystyle M=A+B}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle A={\frac {1}{2}}(M+M^{T})}$   and   ${\displaystyle B={\frac {1}{2}}(M-M^{T})}$

to get voted. The skew-symmetrical matrices then also form a sub-vector space of the matrix space with dimension . The entire -dimensional space can consequently be expressed as a direct sum ${\displaystyle \operatorname {Skew} _{n}}$ ${\displaystyle {\tfrac {n^{2}-n}{2}}}$ ${\displaystyle n^{2}}$ ${\displaystyle K^{n\times n}}$

${\displaystyle K^{n\times n}=\operatorname {Symm} _{n}\oplus \operatorname {Skew} _{n}}$

of the spaces of symmetric and skew-symmetric matrices.

product

The product of two symmetric matrices is in general not symmetric again. The product of symmetrical matrices is symmetrical if and only if and commutate , i.e. if holds, because then it results ${\displaystyle AB}$ ${\displaystyle A,B\in K^{n\times n}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle AB=BA}$

${\displaystyle (AB)^{T}=B^{T}A^{T}=BA=AB}$.

In particular, for a symmetrical matrix , all of its powers with and therefore also its matrix exponential are again symmetrical. For any matrix , both the matrix and the matrix are always symmetric. ${\displaystyle A}$ ${\displaystyle A^{k}}$ ${\displaystyle k\in \mathbb {N} }$ ${\displaystyle e^{A}}$ ${\displaystyle M\in K^{m\times n}}$ ${\displaystyle m\times m}$ ${\displaystyle MM^{T}}$ ${\displaystyle n\times n}$ ${\displaystyle M^{T}M}$

congruence

Any matrix that is congruent to a symmetric matrix is also symmetric because it holds ${\displaystyle B\in K^{n\times n}}$ ${\displaystyle A\in K^{n\times n}}$

${\displaystyle B^{T}=(S^{T}AS)^{T}=S^{T}A^{T}S=S^{T}AS=B}$,

where is the associated transformation matrix. However, matrices that are similar to a symmetric matrix do not necessarily have to be symmetric as well. ${\displaystyle S\in K^{n\times n}}$

Inverse

If a symmetric matrix is invertible , then its inverse is also symmetric again, because it holds ${\displaystyle A\in K^{n\times n}}$ ${\displaystyle A^{-1}}$

${\displaystyle (A^{-1})^{T}=(A^{T})^{-1}=A^{-1}}$.

For a regular symmetric matrix therefore all powers are with symmetrical again. ${\displaystyle A}$ ${\displaystyle A^{-k}}$ ${\displaystyle k\in \mathbb {N} }$

Real symmetric matrices

Symmetric matrices with real entries have a number of other special properties.

normality

A real symmetric matrix is always normal because it holds ${\displaystyle A\in \mathbb {R} ^{n\times n}}$

${\displaystyle A^{T}A=AA=AA^{T}}$.

Every real symmetrical matrix commutes with its transpose. However, there are also normal matrices that are not symmetrical, for example skew-symmetrical matrices.

Self adjointness

A real symmetric matrix is always self-adjoint , because it holds with the real standard scalar product ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ${\displaystyle \langle \cdot ,\cdot \rangle }$

${\displaystyle \langle Ax,y\rangle =(Ax)^{T}y=x^{T}A^{T}y=x^{T}Ay=\langle x,Ay\rangle }$

for all vectors . The converse is also true, and every real self-adjoint matrix is ​​symmetric. Regarded as a complex matrix, a real symmetric matrix is ​​always Hermitian because it holds ${\displaystyle x,y\in \mathbb {R} ^{n}}$

${\displaystyle A^{H}={\bar {A}}^{T}=A^{T}=A}$,

wherein the adjoint matrix to and the conjugated matrix to be. Thus real symmetric matrices are also self-adjoint with respect to the complex standard scalar product . ${\displaystyle A^{H}}$ ${\displaystyle A}$ ${\displaystyle {\bar {A}}}$ ${\displaystyle A}$

Eigenvalues

The unit circle (blue) is transformed into an ellipse (green) by a real symmetrical (2 × 2) matrix. The semi-axes of the ellipse (red) correspond to the amounts of the eigenvalues ​​of the matrix.

The eigenvalues ​​of a real symmetric matrix , that is, the solutions of the eigenvalue equation , are always real. Namely , a complex eigenvalue of with the corresponding eigenvector , then applies the complex self-adjointness of ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ${\displaystyle Ax=\lambda x}$ ${\displaystyle \lambda \in \mathbb {C} }$ ${\displaystyle A}$ ${\displaystyle x\in \mathbb {C} ^{n}}$ ${\displaystyle x\neq 0}$ ${\displaystyle A}$

${\displaystyle \lambda \langle x,x\rangle =\langle \lambda x,x\rangle =\langle Ax,x\rangle =\langle x,Ax\rangle =\langle x,\lambda x\rangle ={\bar {\lambda }}\langle x,x\rangle }$.

After for is, it must hold and the eigenvalue must therefore be real. It then also follows from this that the associated eigenvector can be chosen to be real. ${\displaystyle \langle x,x\rangle \neq 0}$ ${\displaystyle x\neq 0}$ ${\displaystyle \lambda ={\bar {\lambda }}}$ ${\displaystyle \lambda }$ ${\displaystyle x}$

Multiplicities

In every real symmetric matrix, the algebraic and geometric multiples of all eigenvalues ​​match. If namely is an eigenvalue of with geometric multiplicity , then there is an orthonormal basis of the eigenspace of , which can be supplemented by to an orthonormal basis of the total space . With the orthogonal basic transformation matrix, the transformed matrix is ​​obtained ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ${\displaystyle \lambda }$ ${\displaystyle A}$ ${\displaystyle k}$ ${\displaystyle \{x_{1},\ldots ,x_{k}\}}$ ${\displaystyle \lambda }$ ${\displaystyle \{x_{k+1},\ldots ,x_{n}\}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle S=(x_{1}\mid \cdots \mid x_{n})}$

${\displaystyle C=S^{-1}AS=S^{T}AS=\left({\begin{array}{c|c}\lambda I&0\\\hline 0&X\end{array}}\right)}$

as a block diagonal matrix with the blocks and . For the entries of with , namely, with the self-adjointness of and the orthonormality of the basis vectors ${\displaystyle \lambda I\in \mathbb {R} ^{k\times k}}$ ${\displaystyle X\in \mathbb {R} ^{(n-k)\times (n-k)}}$ ${\displaystyle c_{ij}}$ ${\displaystyle C}$ ${\displaystyle \min\{i,j\}\leq k}$ ${\displaystyle A}$ ${\displaystyle x_{1},\ldots ,x_{n}}$

${\displaystyle c_{ij}=\langle x_{i},Ax_{j}\rangle =\langle Ax_{i},x_{j}\rangle =\lambda \langle x_{i},x_{j}\rangle =\lambda \delta _{ij}}$,

where represents the Kronecker delta . Since, by assumption, there are no eigenvectors for the eigenvalue of , there can not be an eigenvalue of . According to the determinant formula for block matrices, the matrix therefore has the eigenvalue exactly with algebraic multiplicity and, due to the similarity of the two matrices, with it . ${\displaystyle \delta _{ij}}$ ${\displaystyle x_{k+1},\ldots ,x_{n}}$ ${\displaystyle \lambda }$ ${\displaystyle A}$ ${\displaystyle \lambda }$ ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle \lambda }$ ${\displaystyle k}$ ${\displaystyle A}$

Diagonalisability

Since algebraic and geometric multiples of all eigenvalues ​​match in a real symmetrical matrix and since eigenvectors are always linearly independent of different eigenvalues , a basis of can be formed from eigenvectors of . Therefore a real symmetric matrix is ​​always diagonalizable , that is, there is a regular matrix and a diagonal matrix such that ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ${\displaystyle A}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle S\in \mathbb {R} ^{n\times n}}$ ${\displaystyle D\in \mathbb {R} ^{n\times n}}$

${\displaystyle S^{-1}AS=D}$

applies. The matrix has the eigenvectors as columns and the matrix has the eigenvalues ​​associated with these eigenvectors on the diagonal . By permutating the eigenvectors, the order of the diagonal entries can be chosen as desired. Therefore two real symmetric matrices are similar to each other if and only if they have the same eigenvalues. Furthermore, two real symmetric matrices can be diagonalized simultaneously if and only if they commute. ${\displaystyle S=(x_{1}\mid \cdots \mid x_{n})}$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle D=\operatorname {diag} (\lambda _{1},\ldots ,\lambda _{n})}$ ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$ ${\displaystyle D}$

Orthogonal diagonalizability

In a symmetrical matrix, the eigenvectors (blue and violet) with different eigenvalues ​​(here 3 and 1) are perpendicular to each other. Applying the matrix, blue vectors are stretched by a factor of three, while purple vectors keep their length.

The eigenvectors for two different eigenvalues ​​of a real symmetric matrix are always orthogonal . It is again true with the self adjointness of ${\displaystyle x_{i},x_{j}}$ ${\displaystyle \lambda _{i}\neq \lambda _{j}}$ ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ${\displaystyle A}$

${\displaystyle \lambda _{i}\langle x_{i},x_{j}\rangle =\langle \lambda _{i}x_{i},x_{j}\rangle =\langle Ax_{i},x_{j}\rangle =\langle x_{i},Ax_{j}\rangle =\langle x_{i},\lambda _{j}x_{j}\rangle =\lambda _{j}\langle x_{i},x_{j}\rangle }$.

Since and were assumed to be different, it then follows . Therefore, an orthonormal basis des can be formed from eigenvectors of . This means that a real symmetric matrix can even be diagonalized orthogonally, that is, there is an orthogonal matrix with which ${\displaystyle \lambda _{i}}$ ${\displaystyle \lambda _{j}}$ ${\displaystyle \langle x_{i},x_{j}\rangle =0}$ ${\displaystyle A}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle S}$

${\displaystyle S^{T}AS=D}$

applies. This representation forms the basis for the principal axis transformation and is the simplest version of the spectral theorem .

Parameters

Due to the diagonalizability of a real symmetric matrix, the following applies to its track ${\displaystyle A\in \mathbb {R} ^{n\times n}}$

${\displaystyle \operatorname {spur} (A)=\lambda _{1}+\ldots +\lambda _{n}}$

and for their determinant accordingly

${\displaystyle \det(A)=\lambda _{1}\cdot \ldots \cdot \lambda _{n}}$.

The rank of a real symmetric matrix is ​​equal to the number of eigenvalues ​​not equal to zero, i.e. with the Kronecker delta

${\displaystyle \operatorname {rang} (A)=n-\left(\delta _{\lambda _{1},0}+\ldots +\delta _{\lambda _{n},0}\right)}$.

A real symmetric matrix is ​​invertible if and only if none of its eigenvalues ​​is zero. The spectral norm of a real symmetric matrix is

${\displaystyle \|A\|_{2}=\max\{|\lambda _{1}|,\ldots ,|\lambda _{n}|\}}$

and thus equal to the spectral radius of the matrix. The Frobenius norm results from normality accordingly to

${\displaystyle \|A\|_{F}={\sqrt {\lambda _{1}^{2}+\ldots +\lambda _{n}^{2}}}}$.

Definiteness

→ Main article : Definiteness

If is a real symmetric matrix, then the expression becomes ${\displaystyle A\in \mathbb {R} ^{n\times n}}$

${\displaystyle Q_{A}(x)=x^{T}Ax=\langle x,Ax\rangle }$

called with square shape of . Depending on whether is greater than, greater than or equal to, less than or less than or equal to zero for all , the matrix is ​​called positive definite, positive semidefinite, negative definite or negative semidefinite. Can have both positive and negative signs, it is called indefinite. The definiteness of a real symmetric matrix can be determined from the signs of its eigenvalues. If all eigenvalues ​​are positive, the matrix is ​​positive definite, if they are all negative, the matrix is ​​negative definite, and so on. The triple consisting of the numbers of positive, negative and zero eigenvalues ​​of a real symmetric matrix is ​​called the signature of the matrix. According to Sylvester's theorem of inertia , the signature of a real symmetric matrix is preserved under congruence transformations . ${\displaystyle x\in \mathbb {R} ^{n}}$ ${\displaystyle A}$ ${\displaystyle Q_{A}(x)}$ ${\displaystyle x\neq 0}$ ${\displaystyle A}$ ${\displaystyle Q_{A}(x)}$ ${\displaystyle A}$

Estimates

According to Courant-Fischer's theorem , the Rayleigh quotient provides estimates for the smallest and the largest eigenvalue of a real symmetric matrix of the form ${\displaystyle A\in \mathbb {R} ^{n\times n}}$

${\displaystyle \min\{\lambda _{1},\ldots ,\lambda _{n}\}\leq {\frac {\langle x,Ax\rangle }{\langle x,x\rangle }}\leq \max\{\lambda _{1},\ldots ,\lambda _{n}\}}$

for everyone with . Equality applies precisely when an eigenvector is the respective eigenvalue. The smallest and the largest eigenvalue of a real symmetrical matrix can accordingly be determined by minimizing or maximizing the Rayleigh quotient. The Gerschgorin circles , which have the form of intervals for real symmetric matrices, offer another possibility for estimating eigenvalues . ${\displaystyle x\in \mathbb {R} ^{n}}$ ${\displaystyle x\neq 0}$ ${\displaystyle x}$

Are two real symmetric matrices with descending sorted eigenvalues and then gives Fan inequality estimate ${\displaystyle A,B\in \mathbb {R} ^{n\times n}}$ ${\displaystyle \lambda _{1}\geq \ldots \geq \lambda _{n}}$ ${\displaystyle \mu _{1}\geq \ldots \geq \mu _{n}}$

${\displaystyle \operatorname {spur} (AB)\leq \lambda _{1}\mu _{1}+\ldots +\lambda _{n}\mu _{n}}$.

Equality is fulfilled if the matrices and can be diagonalized simultaneously in an ordered manner, that is, if an orthogonal matrix exists such that and hold. The Fan inequality represents a tightening of the Cauchy-Schwarz inequality for the Frobenius scalar product and a generalization of the rearrangement inequality for vectors. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle S\in \mathbb {R} ^{n\times n}}$ ${\displaystyle A=S\operatorname {diag} (\lambda _{1},\ldots ,\lambda _{n})S^{T}}$ ${\displaystyle B=S\operatorname {diag} (\mu _{1},\ldots ,\mu _{n})S^{T}}$

Complex symmetric matrices

Disassembly

The decomposition of the complex matrix space as the direct sum of the spaces of symmetrical and skew-symmetrical matrices ${\displaystyle {\mathbb {C} }^{n\times n}}$

${\displaystyle {\mathbb {C} }^{n\times n}=\operatorname {Symm} _{n}\oplus \operatorname {Skew} _{n}}$

represents an orthogonal sum with respect to the Frobenius scalar product. Namely, it holds

${\displaystyle \langle A,B\rangle _{F}=\operatorname {spur} (A^{H}B)=\operatorname {spur} ({\bar {A}}B)=\operatorname {spur} (B{\bar {A}})=\operatorname {spur} ((B{\bar {A}})^{T})=-\operatorname {spur} (A^{H}B)=-\langle A,B\rangle _{F}}$

for all matrices and , from which it follows. The orthogonality of the decomposition also applies to the real matrix space . ${\displaystyle A\in \operatorname {Symm} _{n}}$ ${\displaystyle B\in \operatorname {Skew} _{n}}$ ${\displaystyle \langle A,B\rangle _{F}=0}$ ${\displaystyle {\mathbb {R} }^{n\times n}}$

spectrum

In the case of complex matrices , the symmetry has no particular effect on the spectrum . A complex symmetric matrix can also have non-real eigenvalues. For example, the complex symmetric matrix has ${\displaystyle A\in \mathbb {C} ^{n\times n}}$

${\displaystyle A={\begin{pmatrix}1&i\\i&1\end{pmatrix}}\in \mathbb {C} ^{2\times 2}}$

the two eigenvalues . There are also complex symmetric matrices that cannot be diagonalized. For example, the matrix possesses ${\displaystyle \lambda _{1,2}=1\pm i}$

${\displaystyle A={\begin{pmatrix}1&i\\i&-1\end{pmatrix}}\in \mathbb {C} ^{2\times 2}}$

the only eigenvalue with algebraic multiplicity two and geometric multiplicity one. In general, even any complex square matrix is similar to a complex symmetric matrix. Therefore, the spectrum of a complex symmetrical matrix does not have any special features. The complex counterpart of real symmetric matrices are, in terms of mathematical properties, Hermitian matrices . ${\displaystyle \lambda =0}$

Factorization

Any complex symmetric matrix can be broken down by the Autonne-Takagi factorization ${\displaystyle A\in \mathbb {C} ^{n\times n}}$

${\displaystyle U^{T}AU=D}$

decompose into a unitary matrix , a real diagonal matrix and the transpose of . The entries in the diagonal matrix are the singular values of , i.e. the square roots of the eigenvalues ​​of . ${\displaystyle U\in \mathbb {C} ^{n\times n}}$ ${\displaystyle D=\operatorname {diag} (\sigma _{1},\ldots ,\sigma _{n})\in \mathbb {R} ^{n\times n}}$ ${\displaystyle U}$ ${\displaystyle A}$ ${\displaystyle A^{H}A}$

use

Symmetrical bilinear shapes

If there is a -dimensional vector space over the body , then every bilinear form can be determined by choosing a basis for through the representation matrix ${\displaystyle V}$ ${\displaystyle n}$ ${\displaystyle K}$ ${\displaystyle b\colon V\times V\to K}$ ${\displaystyle \{v_{1},\ldots ,v_{n}\}}$ ${\displaystyle V}$

${\displaystyle A_{b}=(b(v_{i},v_{j}))\in K^{n\times n}}$

describe. If the bilinear form is symmetrical , i.e. if it applies to all , then the representation matrix is also symmetrical. Conversely, every symmetric matrix defines by means of ${\displaystyle b(v,w)=b(w,v)}$ ${\displaystyle v,w\in V}$ ${\displaystyle A_{b}}$ ${\displaystyle A\in K^{n\times n}}$

${\displaystyle b_{A}(x,y)=x^{T}Ay}$

a symmetrical bilinear shape . If a real symmetric matrix is also positive definite, then it represents a scalar product in Euclidean space . ${\displaystyle b_{A}\colon K^{n}\times K^{n}\to K}$ ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ${\displaystyle b_{A}}$ ${\displaystyle \mathbb {R} ^{n}}$

Self-adjoint mappings

If a -dimensional real scalar product space , then every linear mapping can be based on the choice of an orthonormal basis for through the mapping matrix ${\displaystyle (V,\langle \cdot ,\cdot \rangle )}$ ${\displaystyle n}$ ${\displaystyle f\colon V\to V}$ ${\displaystyle \{e_{1},\ldots ,e_{n}\}}$ ${\displaystyle V}$

${\displaystyle A_{f}=(a_{ij})\in \mathbb {R} ^{n\times n}}$

represent, where for is. The mapping matrix is now symmetrical if and only if the mapping is self-adjoint . This follows from ${\displaystyle f(e_{j})=a_{1j}e_{1}+\ldots +a_{nj}e_{n}}$ ${\displaystyle j=1,\ldots ,n}$ ${\displaystyle A_{f}}$ ${\displaystyle f}$

${\displaystyle \langle f(v),w\rangle =(A_{f}x)^{T}y=x^{T}A_{f}^{T}y=x^{T}A_{f}y=x^{T}(A_{f}y)=\langle v,f(w)\rangle }$,

where and are. ${\displaystyle v=x_{1}e_{1}+\ldots +x_{n}e_{n}}$ ${\displaystyle w=y_{1}e_{1}+\ldots +y_{n}e_{n}}$

Projections and reflections

Orthogonal decompositions are described by symmetric matrices

Is again a -dimensional real scalar product space and is a -dimensional subspace of , where the coordinate vectors are an orthonormal basis for , then the orthogonal projection matrix is on this subspace ${\displaystyle (V,\langle \cdot ,\cdot \rangle )}$ ${\displaystyle n}$ ${\displaystyle U}$ ${\displaystyle k}$ ${\displaystyle V}$ ${\displaystyle x_{1},\ldots ,x_{k}}$ ${\displaystyle U}$

${\displaystyle A_{U}=x_{1}x_{1}^{T}+\ldots +x_{k}x_{k}^{T}\in \mathbb {R} ^{n\times n}}$

as the sum of symmetric rank-one matrices also symmetric. The orthogonal projection matrix onto the complementary space is also always symmetrical due to the representation . Using the projection and each vector can be in mutually orthogonal vectors and disassemble. The reflection matrix on a subspace is also always symmetrical. ${\displaystyle U^{\bot }}$ ${\displaystyle A_{U^{\bot }}=I-A_{U}}$ ${\displaystyle A_{U}}$ ${\displaystyle A_{U^{\perp }}}$ ${\displaystyle v\in V}$ ${\displaystyle u\in U}$ ${\displaystyle u^{\perp }\in U^{\perp }}$ ${\displaystyle I-2A_{U}}$ ${\displaystyle U}$

Systems of linear equations

Finding the solution to a linear system of equations with a symmetrical coefficient matrix is simplified if the symmetry of the coefficient matrix is ​​used. Due to the symmetry, the coefficient matrix can be expressed as a product ${\displaystyle Ax=b}$ ${\displaystyle A}$ ${\displaystyle A}$

${\displaystyle A=LDL^{T}}$

write with a lower triangular matrix with all ones on the diagonal and a diagonal matrix . This decomposition is used, for example, in the Cholesky decomposition of positively definite symmetric matrices to calculate the solution of the system of equations. Examples of modern methods for the numerical solution of large linear equation systems with sparse symmetrical coefficient matrices are the CG method and the MINRES method . ${\displaystyle L}$ ${\displaystyle D}$

Polar decomposition

Every square matrix can also be used as a product by means of the polar decomposition ${\displaystyle A\in \mathbb {R} ^{n\times n}}$

${\displaystyle A=QP}$

an orthogonal matrix and a positive semidefinite symmetric matrix . The matrix is the square root of . If regular, then positive is definite and the polar decomposition is clearly with . ${\displaystyle Q\in \mathbb {R} ^{n\times n}}$ ${\displaystyle P\in \mathbb {R} ^{n\times n}}$ ${\displaystyle P}$ ${\displaystyle A^{T}A}$ ${\displaystyle A}$ ${\displaystyle P}$ ${\displaystyle Q=AP^{-1}}$

Applications

geometry

Quadrics can be described by symmetric matrices

A quadric in -dimensional Euclidean space is the set of zeros of a quadratic polynomial in variables. Each quadric can thus be used as a point set of the form ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle Q=\left\{x\in \mathbb {R} ^{n}\mid x^{T}Ax+2b^{T}x+c=0\right\}}$

are described, where with a symmetric matrix, and are. ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ${\displaystyle A\neq 0}$ ${\displaystyle b\in \mathbb {R} ^{n}}$ ${\displaystyle c\in \mathbb {R} }$

Analysis

The characterization of the critical points of a twice continuously differentiable function can be done with the help of the Hesse matrix ${\displaystyle f\colon D\subset \mathbb {R} ^{n}\to \mathbb {R} }$

${\displaystyle H_{f}(x)=\left({\frac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}(x)\right)\in \mathbb {R} ^{n\times n}}$

be made. According to Schwarz's theorem , the Hessian matrix is ​​always symmetrical. Depending on whether it is positive definite, negative definite or indefinite, there is a local minimum , a local maximum or a saddle point at the critical point . ${\displaystyle H_{f}(x)}$ ${\displaystyle x}$

Graph theory

An undirected edge-weighted graph always has a symmetric adjacency matrix

The adjacency matrix of an undirected edge - weighted graph with the node set is through ${\displaystyle A_{G}}$ ${\displaystyle G=(V,E,d)}$ ${\displaystyle V=\{v_{1},\ldots ,v_{n}\}}$

${\displaystyle A_{G}=(a_{ij})\in {\bar {\mathbb {R} }}^{n\times n}}$   With   ${\displaystyle a_{ij}={\begin{cases}d(e)&{\text{falls}}~e=\{v_{i},v_{j}\}\in E\\\infty &{\text{sonst}}\end{cases}}}$

given and thus also always symmetrical. Matrices derived from the adjacency matrix by summation or exponentiation, such as the Laplace matrix , the reachability matrix or the distance matrix , are then symmetrical. The analysis of such matrices is the subject of spectral graph theory .

Stochastics

If a random vector consists of real random variables with finite variance , then is the associated covariance matrix ${\displaystyle X=(X_{1},\ldots ,X_{n})}$ ${\displaystyle n}$ ${\displaystyle X_{1},\ldots ,X_{n}}$

${\displaystyle \Sigma _{X}=\left(\operatorname {Cov} (X_{i},X_{j})\right)\in \mathbb {R} ^{n\times n}}$

the matrix of all pairwise covariances of these random variables. Since for holds, a covariance matrix is ​​always symmetric. ${\displaystyle \operatorname {Cov} (X_{i},X_{j})=\operatorname {Cov} (X_{j},X_{i})}$ ${\displaystyle i,j=1,\ldots ,n}$

Symmetric tensors

Tensors are an important mathematical aid in the natural and engineering sciences, especially in continuum mechanics , because in addition to the numerical value and the unit, they also contain information about orientations in space. The components of the tensor refer to tuples of basis vectors that are linked by the dyadic product “⊗”. Everything that is written above about real symmetric matrices as a whole can be transferred to symmetric tensors of the second order. In particular, they too have real eigenvalues ​​and pairwise orthogonal or orthogonalizable eigenvectors. For symmetric positive definite tensors of the second order, a function value analogous to the square root of a matrix or the matrix exponential is also defined.

The statements about the entries in the matrices cannot simply be transferred to tensors, because with the latter they depend on the basic system used. Only with respect to the standard basis - or more generally an orthonormal basis - can second order tensors be identified with a matrix. In particular, for a symmetric second- order tensor T with respect to an orthonormal basis, the same applies to the entries in its coefficient matrix

${\displaystyle T_{ik}=T_{ki}}$

for all possible combinations of i and k . In general, however, this is not the case.

For the sake of clarity, the general representation is limited to the real three-dimensional vector space, not least because of its particular relevance in the natural and engineering sciences. Every second order tensor can be with respect to two vector space bases and as a sum ${\displaystyle {\vec {a}}^{1,2,3}}$ ${\displaystyle {\vec {b}}^{1,2,3}}$

${\displaystyle \mathbf {T} =\sum _{i,j=1}^{3}T^{ij}{\vec {a}}^{i}\otimes {\vec {b}}^{j}}$

to be written. During the transposition , the vectors are swapped in the dyadic product . The transposed tensor is thus

${\displaystyle \mathbf {T} ^{\top }=\sum _{i,j=1}^{3}T^{ij}{\vec {b}}^{j}\otimes {\vec {a}}^{i}=\sum _{i,j=1}^{3}T^{ji}{\vec {b}}^{i}\otimes {\vec {a}}^{j}}$

A possible symmetry is not so easily recognizable here, in any case the condition is not sufficient for the verification. ${\displaystyle T^{ij}=T^{ji}}$

Even with tensors of higher order, the basis vectors in the tuples are swapped during transposition . However, there are several possibilities to permute the basis vectors and accordingly there are various symmetries for higher level tensors. In a tensor fourth stage is represented by the notation te i-vector with the k-th vector of the reversed, for example, ${\displaystyle {\stackrel {4}{\mathbf {A} }}}$ ${\displaystyle {\stackrel {4}{\mathbf {A} }}{}^{\stackrel {ik}{\top }}}$

${\displaystyle {\stackrel {4}{\mathbf {A} }}=\sum _{i,j,k,l=1}^{3}A_{ijkl}{\hat {e}}_{i}\otimes {\hat {e}}_{j}\otimes {\hat {e}}_{k}\otimes {\hat {e}}_{l}\quad \rightarrow \quad {\stackrel {4}{\mathbf {A} }}{}^{\stackrel {13}{\top }}=\sum _{i,j,k,l=1}^{3}A_{ijkl}{\hat {e}}_{k}\otimes {\hat {e}}_{j}\otimes {\hat {e}}_{i}\otimes {\hat {e}}_{l}}$

When transposing " ^┬ " without specifying the positions, the first two vectors are exchanged for the last two vectors:

${\displaystyle {\stackrel {4}{\mathbf {A} }}{}^{\top }=\sum _{i,j,k,l=1}^{3}A_{ijkl}{\hat {e}}_{k}\otimes {\hat {e}}_{l}\otimes {\hat {e}}_{i}\otimes {\hat {e}}_{j}}$

Symmetries exist when the tensor agrees with its somehow transposed form.

Remarks:

1. ^ H. Altenbach: Continuum Mechanics . Springer, 2012, ISBN 978-3-642-24118-5 , pp. 22 .
2. ^ W. Ehlers: Supplement to the lectures, Technical Mechanics and Higher Mechanics . 2014, p. 25 ( uni-stuttgart.de [PDF; accessed on January 17, 2018]).

See also

• Persymmetric matrix , a matrix that is symmetric about its counter-diagonal
• Centrally symmetric matrix , a matrix that is point-symmetric with respect to its center
• Symmetric operator , a generalization of symmetric matrices to infinite-dimensional spaces
• Symmetric orthogonalization , an orthogonalization method for solving generalized eigenvalue problems

literature

• Gerd Fischer : Linear Algebra. (An introduction for first-year students). 13th revised edition. Vieweg, Braunschweig et al. 2002, ISBN 3-528-97217-3 .
• Roger A. Horn, Charles R. Johnson: Matrix Analysis . Cambridge University Press, 2012, ISBN 0-521-46713-6 .
• Hans-Rudolf Schwarz, Norbert Köckler: Numerical Mathematics. 5th revised edition. Teubner, Stuttgart et al. 2004, ISBN 3-519-42960-8 .

Individual evidence

1. ↑ Christoph W. Überhuber: Computer Numerik . tape 2 . Springer, 1995, p. 401 f .
2. ↑ Howard Anton, Chris Rorres: Elementary Linear Algebra: Applications Version . John Wiley & Sons, 2010, pp. 404-405 .
3. ↑ Jonathan M. Borwein, Adrian S. Lewis: Convex Analysis and Nonlinear Optimization: Theory and Examples . Springer, 2010, ISBN 978-0-387-31256-9 , pp. 10 .
4. ^ Roger A. Horn, Charles R. Johnson: Matrix Analysis . Cambridge University Press, 2012, pp. 271 .
5. ^ Roger A. Horn, Charles R. Johnson: Matrix Analysis . Cambridge University Press, 2012, pp. 153 .

Web links

• TS Pigolkina: Symmetric matrix . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Eric W. Weisstein : Symmetric matrix . In: MathWorld (English).
• Thumb: Symmetric matrix . In: PlanetMath . (English)