CG procedure
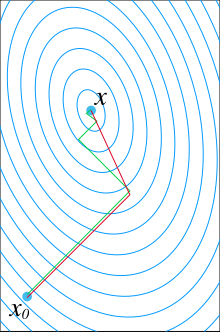
The CG method (of English. C onjugate g radients or conjugate gradient method ) is an efficient numerical method to solve large systems of linear equations of the form with symmetric , positive definite system matrix .
The method delivers, in exact arithmetic, the exact solution after no more than steps, whereby the size of the square matrix is. However, it is particularly interesting as an iterative method , since the error falls monotonically. The CG method can be classified in the class of the Krylow subspace methods .
It was first proposed in 1952 by Eduard Stiefel and Magnus Hestenes . A method that is equivalent for certain systems of equations was also proposed by Cornelius Lanczos in the early 1950s with the Lanczos method .
Idea of the CG process
The idea of the CG method is that for symmetric and positive definites the minimization of the square shape
is equivalent to solving . This is the standard scalar product .
The gradient of at this point is straight and can therefore be calculated quickly for large, sparsely populated matrices . The idea of the CG method is now to minimize the function over a subspace instead of in the direction of the residual as in the gradient method in another direction . The directions are all conjugated , that is, it applies
- .
The iterates of the CG method are then chosen such that they form the minimum of in the affine space that is spanned by the vectors and shifted by:
It can be shown that the following also applies:
The last part shows that the search directions span the Krylow space to A and . The CG method can therefore alternatively be defined directly as a Krylow subspace method.
Since the vectors are all -conjugated, the dimension of is even if the vectors are. You can show that is when is. If there is a matrix, the process terminates after steps at the latest , if the calculation is precise. Numerical errors can be eliminated by further iterations. To do this, consider the gradient that specifies the residual. If the norm of this residual falls below a certain threshold value, the process is terminated.
The process gradually builds an orthogonal basis for the and minimizes it as best as possible in the respective direction.
The problem with the iterative method is finding the optimal step size. In order to determine the quality of a point, a complete matrix multiplication is necessary, which at the same time delivers a new gradient. If the step size along a given gradient is too imprecise, the method corresponds more to a simple mountain climbing algorithm .
CG process without preconditioning
First you choose any and calculate:
For one executes:
- Save matrix-vector-product to calculate it just once
- Find from in the direction of the location of the minimum of the function and update the gradient or the residual
- Correct the search direction using and
until the residual in the norm is less than a tolerance ( ).
variants
There are different variants of the process, in addition to the first one by Roger Fletcher and Colin Reeves z. B. by Hestenes and Stiefel, by Davidon , Fletcher and Powell or by Polak and Ribière. These are identical for quadratic forms (as defined above), since the other terms vanish due to the orthogonality of the residuals. However, if the CG method is used to minimize a function approximated by a square shape, these variants often show better convergence behavior than the original formulation by Fletcher and Reeves.
- (Fletcher-Reeves)
- (Polak-Ribière)
- (Hestenes boots)
CG process with symmetrical preconditioning (PCG process)
The convergence of the CG method is only assured with symmetrical positive definite matrices. A preconditioner must take this into account. In a symmetrical preconditioning, the equation system is by means of a preconditioner matrix to with transformed and then applied the CG process.
The matrix is symmetrical because is symmetrical. It is also positive definite, since according to Sylvester's law of inertia and have the same numbers of positive and negative eigenvalues .
The resulting procedure is the so-called PCG procedure (from English P reconditioned C onjugate G radient):
First you choose any and calculate:
For one sets:
- Save matrix-vector-product to calculate it just once
- Find from towards the minimum and update gradients and preconditioned gradients
- ( Residual )
- Correct the search direction
until the residual in the norm is less than a tolerance ( ).

A common preconditioner associated with CG is the incomplete Cholesky decomposition . This combination is also known as ICCG and was introduced by Meijerink and van der Vorst in the 1970s .
Two further preconditioners permitted for the PCG method are the Jacobi preconditioner , where the main diagonal is from , and the SSOR preconditioner
with , where the main diagonal and the strict lower triangular matrix of is.
Convergence rate of the CG method
It can be shown that the convergence speed of the CG method is through
is described. Here is the condition of the matrix with respect to the spectral norm, i.e. the matrix norm generated by the Euclidean norm, as well as the energy norm of . The expression is not negative, because the condition number (with regard to a matrix norm generated by a vector norm) of a matrix is always greater than or equal to 1. Since symmetric and positive is definite, the following applies
- .
From the minimization property it can also be deduced that
- ,
where any polynomial is of degree with and the solution. With that is spectrum , so the amount of the eigenvalues of matrix meant. It follows that the CG method solves a system into a matrix with only different eigenvalues in steps and that the CG method converges very quickly for systems in which the eigenvalues are concentrated in a few small surroundings. This in turn provides a clue for useful preconditioners: A preconditioner is good if it ensures that the eigenvalues are concentrated.
Extension to asymmetrical matrices
If the system matrix A is asymmetrical but regular , the CG method can be based on the normal equations
can be applied, since for a regular matrix A is symmetric and positive definite. This procedure is also called CGNR, since this procedure minimizes the norm of the residual of . Alternatively, there is the CGNE procedure, which
solves with . The error is minimized here.
Both methods have the disadvantage that, on the one hand , what is not always given must be available and, on the other hand, the condition of A is squared in this approach, which can lead to a slowdown in convergence.
literature
- CT Kelley: Iterative Methods for Linear and Nonlinear Equations. SIAM, ISBN 0-89871-352-8 . PDF (783 kB)
- P. Knabner, L. Angermann: Numerics of partial differential equations. Springer, ISBN 3-540-66231-6 .
- A. Meister: Numerics of linear systems of equations. Vieweg 1999, ISBN 3-528-03135-2 .
- William H., Teukolsky, Saul A .: Numerical Recipes in C ++. Cambridge University Press 2002, ISBN 0-521-75033-4 .
- JR Shewchuck: An Introduction to the Conjugate Gradient Method Without the Agonizing Pain (PDF) (503 kB).
- Eduard Stiefel : About some relaxation calculation methods. ZAMP, 3 (1), 1-33, 1952.
Individual evidence
- ↑ Hestenes, Stiefel: Methods of conjugate gradients for solving linear systems , Journal of Research of the National Bureau of Standards, Vol. 49, 1952, pp. 409-436, doi : 10.6028 / jres.049.044






























![{\ begin {aligned} \ alpha _ {k} \; & = \; {\ frac {r_ {k} ^ {T} r_ {k}} {d_ {k} ^ {T} \, z}}, \\ [. 2em] x_ {k + 1} \; & = \; x_ {k} + \ alpha _ {k} d_ {k}, \\ [. 4em] r_ {k + 1} \; & = \; r_ {k} - \ alpha _ {k} z \ end {aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f2dfa3155ee358d08f8e3c9d56dc22bd44bc670)


![{\ begin {aligned} \ beta _ {k} \; & = \; {\ frac {r_ {k + 1} ^ {T} r_ {k + 1}} {r_ {k} ^ {T} r_ { k}}}, \\ [. 2em] d_ {k + 1} \; & = \; r_ {k + 1} + \ beta _ {k} d_ {k}, \ end {aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9358596176e5349ae1fb5a3feb950d247ea2ed16)





















![C = \ left [{\ tfrac {1} {2- \ omega}} \ left ({\ tfrac {1} {\ omega}} D + L \ right) \ left ({\ tfrac {1} {\ omega }} D \ right) ^ {- 1} \ left ({\ tfrac {1} {\ omega}} D + L \ right) ^ {T} \ right] ^ {- 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc3222086d7cf28ddb44e5f539a5aadbe85bff7)

















