Gradient method

The gradient method is used in numerics to solve general optimization problems. In doing so, one proceeds (using the example of a minimization problem) from a starting point along a direction of descent until no further numerical improvement is achieved. If the negative gradient is selected as the direction of descent, i.e. the direction of the locally steepest descent, the method of the steepest descent is obtained . Sometimes the terms gradient method and steepest descent method are used interchangeably. In general, the gradient method denotes an optimization method in which the direction of descent is obtained from gradient information, that is, it is not necessarily limited to the negative gradient.

The steepest descent procedure often converges very slowly as it approaches the stationary point with a strong zigzag course. Other methods for calculating the direction of descent sometimes achieve significantly better convergence speeds , for example the conjugate gradient method is suitable for solving symmetrically positive definite linear systems of equations . The gradient descent is connected to the hill climbing ( hill climbing ) is used.

The optimization problem

The gradient method can be used to minimize a real-valued, differentiable function : ${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }$

${\displaystyle {\underset {x\in \mathbb {R} ^{n}}{\min }}\ f(x).}$

This is a problem of optimization without constraints, also called an unrestricted optimization problem .

The procedure

Starting from a starting point, the gradient method generates a sequence of points according to the iteration rule ${\displaystyle x^{0}\in \mathbb {R} ^{n}}$ ${\displaystyle x^{k}\in \mathbb {R} ^{n}}$

${\displaystyle x^{k+1}=x^{k}+\alpha ^{k}d^{k},\quad k=0,1,\ldots }$

where is a positive step size and a direction of descent . Both and in each iteration step are determined in such a way that the sequence converges to a stationary point of . ${\displaystyle \alpha ^{k}>0}$ ${\displaystyle d^{k}\in \mathbb {R} ^{n}}$ ${\displaystyle \alpha ^{k}}$ ${\displaystyle d^{k}}$ ${\displaystyle x^{k}}$ ${\displaystyle f}$

Determine the direction of descent

Descent directions have an angle greater than 90 ° with the gradient in the point . The dashed straight line is the tangent to the isoline of the two-dimensional function, it represents the limit case in which the angle with the gradient is 90 °. The direction of descent points in the direction of the negative gradient, i.e. H. towards the steepest descent. ${\displaystyle d_{i}}$ ${\displaystyle x}$ ${\displaystyle d_{2}}$

A direction of descent in the point is a vector that ${\displaystyle x^{k}}$ ${\displaystyle d^{k}}$

${\displaystyle \left(\nabla f(x^{k})\right)^{T}d^{k}<0}$

Fulfills. Intuitively, this means that the angle between and is greater than 90 °. Since the gradient points in the direction of the steepest rise, there is a direction along which the function value decreases. ${\displaystyle \nabla f(x^{k})}$ ${\displaystyle d^{k}}$ ${\displaystyle \nabla f(x^{k})}$ ${\displaystyle d^{k}}$

Many gradient methods use it to calculate the direction of descent

${\displaystyle d^{k}=-D^{k}\nabla f(x^{k}),}$

where is a positive definite matrix. In this case, the condition for the direction of descent is ${\displaystyle D^{k}}$

${\displaystyle \left(\nabla f(x^{k})\right)^{T}\left(-D^{k}\right)\nabla f(x^{k})<0,}$

and is always fulfilled thanks to the positive definiteness . ${\displaystyle D^{k}}$

With the choice of the matrix the following algorithms are obtained: ${\displaystyle D^{k}}$

• ${\displaystyle D^{k}=I}$, where is the identity matrix , gives the steepest descent method . The Absteigsrichtung in this case is just the negative gradient, . ${\displaystyle I}$ ${\displaystyle d^{k}=-\nabla f(x^{k})}$
• ${\displaystyle D^{k}={\begin{bmatrix}a_{1}&0&\cdots &0\\0&a_{2}&\ddots &\vdots \\\vdots &\ddots &\ddots &0\\0&\cdots &0&a_{n}\end{bmatrix}}}$, where so positive is definite, is a diagonally scaled steepest descent . They are often chosen as an approximation of the inverse of the 2nd derivative, that is . ${\displaystyle a_{i}>0,\ i=1,\ldots ,n}$ ${\displaystyle D^{k}}$ ${\displaystyle a_{i}}$ ${\displaystyle a_{i}\approx \left({\frac {\partial ^{2}f(x^{k})}{\left(\partial x_{i}\right)^{2}}}\right)^{-1}}$
• ${\displaystyle D^{k}=\left(\nabla ^{2}f(x^{k})\right)^{-1}}$, the inverse Hesse matrix , gives Newton's method for solving nonlinear minimization problems.
• Since the calculation of the Hessian matrix is ​​often complex, there is a class of algorithms which use an approximation . Such methods are called quasi-Newton methods ; there are different ways in which the approximation is calculated. An important representative from the class of quasi-Newton methods is the BFGS algorithm . ${\displaystyle D^{k}\approx \left(\nabla ^{2}f(x)\right)^{-1}}$
• If the optimization problem is given in the special form , i.e. as the sum of squares of functions, one obtains the Gauss-Newton method with , where the Jacobi matrix of is in the point . ${\displaystyle \min _{x\in \mathbb {R} ^{n}}\left\{\|f(x)\|^{2}=\sum _{i=1}^{m}\left(f_{i}(x)\right)^{2}\right\}}$ ${\displaystyle D^{k}=\left(J^{T}J\right)^{-1}}$ ${\displaystyle J}$ ${\displaystyle f}$ ${\displaystyle x^{k}}$

Determine the step size

The determination of the step size is an important part of the gradient method, which can have a great influence on the convergence. Starting from iteration considering the value of along the line , that is . In this context, one often speaks of a line search . The ideal choice would be to calculate the step size as the value that minimizes the function , i.e. the one-dimensional problem ${\displaystyle \alpha ^{k}}$ ${\displaystyle x^{k+1}=x^{k}+\alpha ^{k}d^{k}}$ ${\displaystyle f}$ ${\displaystyle x^{k}+\alpha d^{k}}$ ${\displaystyle f(\alpha )=f(x^{k}+\alpha d^{k})}$ ${\displaystyle f(\alpha )}$

${\displaystyle \min _{\alpha >0}\left\{f(\alpha )=f(x^{k}+\alpha d^{k})\right\}}$

to solve. This is referred to as an exact line search and is rarely used in this form in practice, since even for simple optimization problems the exact determination of the step size is very computationally expensive.

As an alternative to the exact line search, the requirements are relaxed and the function value is reduced “sufficiently” with each iteration step. This is also known as an inexact line search . The simplest possibility is to reduce the step size starting from a start value (e.g. ) until it is reached. This method often works satisfactorily in practice, but it can be shown that for some pathological functions this line search reduces the function value in each step, but the sequence does not converge to a stationary point. ${\displaystyle \alpha }$ ${\displaystyle \alpha =1}$ ${\displaystyle f(x^{k+1})=f(x^{k}+\alpha d^{k})<f(x^{k})}$ ${\displaystyle x^{k}}$

Armijo condition

The Armijo condition formalizes the concept "sufficient" in the required reduction of the function value. The condition is modified to ${\displaystyle f(x^{k}+\alpha d^{k})<f(x^{k})}$

${\displaystyle f(x^{k}+\alpha d^{k})\leq f(x^{k})+\sigma \alpha \left(\nabla f(x^{k})\right)^{T}d^{k},}$

with . The Armijo condition circumvents the convergence problems from the previous simple condition by requiring that the reduction is at least proportional to the step size and the direction derivative , with a proportionality constant . In practice, very small values ​​are often used, e.g. B. . ${\displaystyle \sigma \in (0,1)}$ ${\displaystyle \left(\nabla f(x^{k})\right)^{T}d^{k}}$ ${\displaystyle \sigma }$ ${\displaystyle \sigma =10^{-4}}$

Backtracking line search

The Armijo condition always applies when the step size is sufficiently small and can thus lead to a standstill of the gradient process - the step is so small that no more significant progress is made. A simple combination of repeated reduction of the step size and the Armijo condition is the backtracking line search. It ensures that the step size is small enough to meet the Armijo condition, but on the other hand not too small. In pseudocode:

Wähle Startwert für  ${\displaystyle \alpha }$, z. B.  ${\displaystyle \alpha =1}$, wähle Konstanten  ${\displaystyle \sigma \in (0,1),\ \rho \in (0,1)}$

while  ${\displaystyle f(x^{k}+\alpha d^{k})>f(x^{k})+\sigma \alpha \left(\nabla f(x^{k})\right)^{T}d^{k}}$
   ${\displaystyle \alpha =\rho \alpha }$
end

Setze  ${\displaystyle \alpha ^{k}=\alpha }$

The backtracking line search repeatedly reduces the step size by the factor until the Armijo condition is met. It is guaranteed to terminate after a finite number of steps and is often used in practice because of its simplicity. ${\displaystyle \rho }$

convergence

In general, the gradient method converges neither to a global nor to a local minimum. Only the convergence to a stationary point , i.e. a point with , can be guaranteed . If one restricts the class of objective functions to convex functions , stronger guarantees are possible, see convex optimization . ${\displaystyle x^{*}}$ ${\displaystyle \nabla f(x^{*})=0}$

Convergence speed

For the general case, a statement can neither be made about the speed of convergence of the sequence nor about the speed of convergence of the sequence . If is a Lipschitz constant of , one can show that the norm of the gradients converges towards 0 with the rate , where is a positive constant. ${\displaystyle \{f(x^{k})\}}$ ${\displaystyle \{x^{k}\}}$ ${\displaystyle L}$ ${\displaystyle \nabla f}$ ${\displaystyle g_{N}^{*}=\min _{0\leq k\leq N}\|\nabla f(x^{k})\|}$ ${\displaystyle {\sqrt {\frac {L\left(f(x^{0})-f(x^{*})\right)}{\omega (N+1)}}}}$ ${\displaystyle \omega >0}$

example

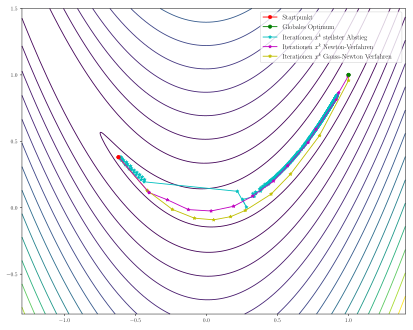
The Rosenbrock function with ${\displaystyle a=1,\ b=100}$

The Rosenbrock function

${\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} :x\mapsto \left(a-x_{1}\right)^{2}+b\left(x_{2}-x_{1}^{2}\right)^{2}}$

is often used as a test for optimization methods because it is challenging because of the narrow and shallow valley in which iterative methods can only take small steps. The constants are usually chosen with , the global optimum in this case is with the function value . ${\displaystyle a=1,\ b=100}$ ${\displaystyle x^{*}=(1,1)}$ ${\displaystyle f(x^{*})=0}$

The gradient and the Hessian matrix result as

${\displaystyle \nabla f={\begin{bmatrix}4bx_{1}^{3}-4bx_{1}x_{2}+2(x_{1}-a)\\2b(-x_{1}^{2}+x_{2})\end{bmatrix}}}$

such as

${\displaystyle \nabla ^{2}f={\begin{bmatrix}12bx_{1}^{2}-4bx_{2}+2&-4bx_{1}\\-4bx_{1}&2b\end{bmatrix}}}$.

This allows the algorithms of the steepest descent and Newton's method to be implemented directly. In order to apply the Gauss-Newton method , the Rosenbrock function must first be brought into the form “sum of squares of functions”. This is explained in detail on the page on the Gauss-Newton method .

Optimization with procedures of the steepest descent, Newton procedure and Gauss-Newton procedure

For line search backtracking is used in all procedures with the following parameters used: start value , , . The starting point is chosen. ${\displaystyle \alpha =1}$ ${\displaystyle \rho =0{,}5}$ ${\displaystyle \sigma =0{,}001}$ ${\displaystyle x^{0}=(-0{,}62;\,0{,}38)}$

Even after 1000 iterations, the process of the steepest descent does not find the global optimum and is stuck in the flat valley, where only very small steps are possible. In contrast, both the Newton method and the Gauss-Newton algorithm find the global optimum in just a few iterations.

See also

• Line search method

literature

• Yurii Nesterov: Introductory Lectures on Convex Optimization: A Basic Course. Springer Science & Business Media, 2003, ISBN 1-4419-8853-X .
• Dimitri P. Bertsekas: Nonlinear Programming. 2nd Edition. Athena Scientific, 1995, ISBN 1-886529-14-0 .
• Jorge Nocedal, Stephen Wright: Numerical Optimization. Springer Science & Business Media, 2000, ISBN 0-387-98793-2 .
• Andreas Meister: Numerics of linear systems of equations. 2nd Edition. Vieweg, Wiesbaden 2005, ISBN 3-528-13135-7 .

Individual evidence

1. ↑ Dimitri P. Bertsekas: Nonlinear programming . 3. Edition. Athena Scientific, 2016, ISBN 978-1-886529-05-2 .