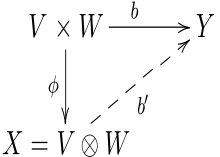Tensor
A tensor is a linear mathematical function that maps a certain number of vectors to a numerical value. It is a mathematical object from linear algebra that is particularly used in the field of differential geometry . The term was originally introduced in physics and only later made more precise mathematically.
In differential geometry and the physical disciplines, tensors in the sense of linear algebra are usually not considered, but rather tensor fields are dealt with, which are often also referred to as tensors for simplicity. A tensor field is a map that assigns a tensor to every point in space. Many physical field theories deal with tensor fields. The most prominent example is general relativity . The mathematical sub-area that deals with the investigation of tensor fields is called tensor analysis and is an important tool in the physical and engineering disciplines.
Concept history
The word tensor (derived from the past participle from Latin tendere ' to span' ) was introduced to mathematics by William Rowan Hamilton in the 1840s ; he used it to denote the absolute value of his quaternions , not a tensor in the modern sense. James Clerk Maxwell does not seem to have called the stress tensor , which he transferred from elasticity theory to electrodynamics , himself.
In its modern meaning, as a generalization of scalar , vector , matrix , the word tensor is first introduced by Woldemar Voigt in his book The fundamental physical properties of crystals in elementary representation (Leipzig, 1898).
Under the title absolute differential geometry , Gregorio Ricci-Curbastro and his student Tullio Levi-Civita developed the tensor calculus on Riemannian manifolds around 1890 ; They made their results accessible to a larger specialist audience in 1900 with the book Calcolo differenziale assoluto , which was soon translated into other languages, and from which Albert Einstein acquired the mathematical foundations he needed to formulate the general theory of relativity . Einstein himself coined the term tensor analysis in 1916 and, with his theory, contributed significantly to popularizing the tensor calculus; In addition, he introduced Einstein's sums convention , according to which double indices are added, omitting the sums symbols.
Types of tensors

Starting from a finite-dimensional vector space, scalars are called type tensors , column vectors are type tensors, and covectors (or row vectors) are type tensors . Higher level tensors are defined as multilinear mappings with lower level tensors as arguments and map values. For example, a tensor of the type can be understood as a linear mapping between vector spaces or as a bilinear mapping with a vector and a covector as arguments.
For example, the mechanical stress tensor in physics is a second order tensor - a number (strength of the stress ) or a vector (a main stress direction ) are not always sufficient to describe the stress state of a body . As a tensor of the type , it is a linear mapping which assigns the force acting on it (as a covector) to a surface element (as a vector), or a bilinear mapping which assigns the work that occurs during the displacement of the surface area to a surface element and a displacement vector the influence of the acting voltage is performed.
With regard to a fixed vector space basis , the following representations of the different types of tensors are obtained:
- A scalar by a single number.
- One vector by one column vector.
- A co-vector by a line vector.
- A second order tensor through a matrix.
The application of the stress tensor to a surface element is then z. B. given by the product of a matrix with a column vector. The coordinates of higher order tensors can be arranged accordingly in a higher dimensional scheme. Unlike those of a column vector or a matrix, these components of a tensor can have more than one or two indices. An example of a third order tensor that has three vectors des as arguments is the determinant of a 3 × 3 matrix as a function of the columns of that matrix. With respect to an orthonormal basis , it is represented by the Levi-Civita symbol .
Co- and contravariance of vectors
The terms co- and contravariant refer to the coordinate representations of vectors, linear forms and are also applied to tensors as described later in the article. They describe how such coordinate representations behave with regard to a base change in the underlying vector space.
If a basis is established in a -dimensional vector space , each vector of this space can be represented by a number tuple - its coordinates - by means of . If you move to a different base from , the vector itself does not change, but the coordinates with respect to the new base will be different. If the new base is determined by in the old base, the new coordinates are obtained by comparing in
so or
- .
For example, if one rotates an orthogonal base in a three-dimensional Euclidean space around the -axis, the coordinate vectors in the coordinate space also rotate around the -axis, but in the opposite direction . This transformation behavior opposite to the basic transformation is called contravariant. Vectors to abbreviate the notation are often identified with their coordinate vectors, so that vectors are generally referred to as contravariant.
A linear form or a covector , on the other hand, is a scalar-valued linear mapping on vector space. You can assign it as coordinates its values on the basis vectors ,,. The coordinate vectors of a linear form transform like the base tuple as
which is why this transformation behavior is called covariant . If one again identifies linear forms with their coordinate vectors, one also generally designates linear forms as covariant. As with vectors, the underlying basis emerges from the context. In this context, one also speaks of dual vectors.
These names are transferred to tensors. This is explained in the next section on the definition of the tensors.
definition
( r , s ) -tensor space
In the following, all vector spaces are finite-dimensional. With denotes the set of all linear forms from the vector space into the body . Are vector spaces over , the vector space of going multi-linear forms with designated.
If a - vector space is called its dual space . Then is isomorphic to the tensor product
- (compare the section on tensor products and multilinear forms ).
Now set for a fixed vector space with dual space
with entries from and entries from . This vector space realizes the tensor product
Elements of this set are called tensors, contravariant of level and covariant of level . In short, one speaks of type tensors . The sum is called the level or rank of the tensor.
There are natural isomorphisms of the following types:
This means that one can also inductively define tensors of the level as multilinear mappings between tensor spaces of lower level. There are several equivalent possibilities for a tensor of a certain type.
In physics, the vector spaces are usually not identical, e.g. B. one cannot add a velocity vector and a force vector. However, one can compare the directions with one another, i. that is, identify the vector spaces with one another except for a scalar factor . Hence the definition of tensors of type can be applied accordingly. It should also be mentioned that (dimensional) scalars in physics are elements of one-dimensional vector spaces and that vector spaces with a scalar product can be identified with their dual space. One works z. B. with force vectors, although forces without the use of the scalar product are to be regarded as covectors.
External tensor product
An (outer) tensor product or tensor multiplication is a link between two tensors. Let be a vector space and be and tensors. The (outer) tensor product of and is the tensor passed through
is defined. Here are those and those .
Examples of ( r , s ) -tensors
In the following, let and be finite-dimensional vector spaces.
- The set of (0,0) -tensors is isomorphic to the underlying field . You do not assign a body element to any linear shape or vector. Hence the designation as (0,0) -tensors.
- (0.1) -tensors organize any linear form and a vector to a number, thus correspond to the linear forms on .
- (1,0) -tensors assign a number to a linear form and not to a vector. They are therefore elements of the bidual vector space . In the case of finite-dimensional ones, they correspond to the initial vector spaces , since the following applies here (see isomorphism ).
- A linear mapping between finite-dimensional vector spaces can be understood as an element of and is then a (1,1) -tensor.
- A bilinear form can be understood as an element of, i.e. as a (0,2) -tensor. In particular, scalar products can be interpreted as a (0.2) -tensor.
- The Kronecker delta is again a (0.2) tensor. It is an element of and therefore a multilinear mapping . Multilinear mappings are uniquely determined by the effect on the basis vectors. The Kronecker Delta is clearly through
- certainly.
- The determinant of matrices, interpreted as the alternating multilinear form of the columns, is a (0, n) -tensor. With regard to an orthonormal basis, it is represented by the Levi-Civita symbol ("epsilon tensor"). Especially in three dimensions, the determinant is a third order tensor and it applies to the elements of an orthonormal basis. Both the Kronecker delta and the Levi-Civita symbol are widely used to study symmetry properties of tensors. The Kronecker delta is symmetric when the indices are swapped, the Levi-Civita symbol is antisymmetric, so that tensors can be broken down into symmetric and antisymmetric parts with their help.
- Another example of a second order covariant tensor is the inertia tensor .
- In elasticity theory , Hooke's equation is generalized about the relationship between forces and associated strains and distortions in an elastic medium, also with the help of tensor calculus by introducing the distortion tensor , which describes distortions, deformations, and the stress tensor , which describes the forces causing the deformations. See also under continuum mechanics .
- Let be a vector space with a scalar product . As mentioned above, the scalar product is linear in both arguments, i.e. a (0.2) -tensor or a two-fold covariant tensor. One also speaks of a metric tensor or a “metric” for short. It should be noted that it is not a metric itself in the sense of a metric space , but creates one. The coordinates of the metric with respect to a basis of the vector space are denoted by; and be the coordinates of the vectors and with respect to the same basis. The following therefore applies to the mapping of two vectors and below the metric
- The transition between co- and contravariant tensors can be passed through by means of the metric
- accomplish.
- In differential geometry on Riemannian manifolds , this metric is also a function of location. A tensor-valued function of the location is called a tensor field , in the case of the metric tensor specifically a Riemannian metric.
- In the theory of pseudo-Riemannian manifolds , the concept of the metric tensor is generalized in such a way that the definition of the scalar product is dispensed with. The most important application is the theory of relativity . In the special theory of relativity , the improper metric of the Minkowski space is used instead of the Euclidean metric . In general relativity , a tensor field with the same signature as the Minkowski metric is used.
Base
Basis and dimension
Let be a vector space as above, then the spaces are also vector spaces. Furthermore, let now be finite dimensional with the base . The dual basis is denoted by. The space of the tensors is then also finite dimensional and
is a basis of this space. That means every element can go through
being represented. The dimension of this vector space is . As in every finite-dimensional vector space, in the space of tensors it is sufficient to say how a function operates on the basis.
Since the above sums display involves a lot of paperwork, Einstein's sums convention is often used. So in this case you write
The coefficients are called components of the tensor with respect to the base . Often one identifies the components of the tensor with the tensor itself. See under tensor representations in physics .
Base change and coordinate transformation
Let and be different bases of the vector spaces . Every vector, including every basis vector, can be represented as a linear combination of the basis vectors . The basis vector is represented by
The sizes thus determine the basis transformation between the bases and . That goes for everyone . This process is called a change of base .
Let the components of the tensor be with respect to the base . The equation then results for the transformation behavior of the tensor components
As a rule, a distinction is made between the coordinate representation of the tensor and the transformation matrix . The transformation matrix is an indexed quantity, but not a tensor. In Euclidean space these are rotation matrices and in special relativity z. B. Lorentz transformations , which can also be understood as "rotations" in a four-dimensional Minkowski space . In this case one also speaks of four-tensors and four-vectors .
example
With the help of the components, a tensor can be represented with respect to a basis. For example, a tensor with rank 2 in a given basis system can be represented as a matrix as follows:
This allows the value to be calculated within the framework of the corresponding basic system with the help of matrix multiplication :
If one now looks specifically at the inertia tensor , it can be used to calculate the rotational energy of a rigid body with the angular velocity with respect to a selected coordinate system as follows:
Operations on tensors
Besides the tensor product there are other important operations for (r, s) -tensors.
Inner product
The inner product of a vector (or a (co-) vector ) with a tensor is the (or ) -tensor that passes through
or through
is defined. This means that the tensor is evaluated on a fixed vector or fixed covector .
Tensor taper
Given are an (r, s) -tensor and and . The tensor taper forms the tensor
on the tensor
from. This process is called tensor tapering or track formation. In the case of (1,1) tensors, the tensor taper corresponds to
identifying the trace of an endomorphism.
With the help of Einstein's summation convention, the tensor taper can be represented very briefly. For example, be the coefficients (or coordinates) of the two-stage tensor with respect to a chosen basis. If one wants to taper this (1,1) -tensor, one often writes instead of just the coefficients . Einstein's summation convention now states that all identical indices are summed up and thus is a scalar that corresponds to the trace of the endomorphism. The expression , on the other hand, is not defined, because the same indices are only added if one is above and one below. On the other hand, it is a first order tensor.
Pull-back (return transport)
Let be a linear mapping between vector spaces that need not be an isomorphism. The return of is a figure that through
is defined. There is and .
Push forward
Let be a vector space isomorphism . Define the push forward from through with
There is , and . With the will return transport of the linear form listed. In concrete terms this means . As with the return transport, the isomorphism of can be dispensed with with push forward and this operation can only be defined for tensors.
Tensor algebra
Let be a vector space over a body . Then it's through
defines the so-called tensor algebra. With the multiplication given by the tensor product on the homogeneous components , it becomes a unitary associative algebra .
Tensor product space
In this section tensor product spaces are defined. These are typically considered in algebra . This definition is more general than that of the (r, s) -tensors, since here the tensor spaces can be constructed from different vector spaces.
The universal quality
Let and vector spaces over the field . If there are additional vector spaces, any bilinear mapping and a linear mapping, then the link is also a bilinear mapping. If a bilinear mapping is given, then any number of other bilinear maps can be constructed from it. The question that arises is whether there is a bilinear map from which, in this way, by combining with linear maps, all bilinear maps can be constructed in a (unambiguous way). Such a universal object, i. H. the bilinear mapping including its image space is called the tensor product of and .
Definition: As the tensor product of the vector spaces and , every vector space is called, for which there is a bilinear map that fulfills the following universal property :
- At any bilinear mapping of in a vector space there exists a linear map such that for all true
If there is such a vector space , it is unique except for isomorphism . One writes and . So the universal property can be written as. For the construction of such product spaces, reference is made to the article Tensor product .
Tensor as an element of the tensor product
In mathematics tensors are elements of tensor products.
Let it be a body and there are vector spaces above the body .
The tensor product of is a vector space whose elements are sums of symbols of the form
are. The following calculation rules apply to these symbols:
The tensors of the form are called elementary. Every tensor can be written as the sum of elementary tensors, but this representation is not unique except in trivial cases, as can be seen from the first of the two calculation rules.
If there is a basis of (for ; ), then is
a basis of The dimension of is therefore the product of the dimensions of the individual vector spaces
Tensor products and multilinear forms
The dual space of can with the space of - multilinear forms
be identified:
- If a linear form is on , the corresponding multilinear form is
- If a -Multilinearform is, then the corresponding linear form is defined by
If all the vector spaces considered are finite dimensional, one can
identify with each other, d. i.e. , elements of corresponding multi-linear forms
Invariants of tensors 1st and 2nd order
The invariants of a one- or two-stage tensor are scalars that do not change under orthogonal coordinate transformations of the tensor. For tensors of the first order, the formation of the norm induced by the scalar product leads to an invariant
- ,
Here and in the following, Einstein's summation convention is used again. For second order tensors in three-dimensional Euclidean space, six irreducible invariants (i.e. invariants that cannot be expressed by other invariants) can generally be found:
In the case of symmetric 2nd order tensors (e.g. the strain tensor ) the invariants and coincide. In addition, the other 3 invariants can be represented (so it is no longer irreducible). The determinant is also an invariant; it can be represented, for example, for matrices over the irreducible invariants , and as
For antisymmetric tensors applies , , and can be again attributed. Thus, in the three-dimensional Euclidean space, symmetric tensors 2nd level have three irreducible invariants and antisymmetric tensors 2nd level have one irreducible invariant.
Tensor products of a vector space and symmetry
One can build the tensor product of a vector space with itself. Without further knowledge of the vector space, an automorphism of the tensor product can be defined, which consists in exchanging the factors in the pure products :
Since the square of this mapping is the identity, it follows that only the values come into question for the eigenvalues .
- One that fulfills is called symmetrical. Examples are the elements
- .
- The set of all symmetric tensors of level 2 is denoted by.
- One that fulfills is called antisymmetric or alternating. Examples are the elements
- .
- The set of all antisymmetric tensors of level 2 is denoted by.
Using tensor powers of any level can be formed. Correspondingly, further exchanges in pairs can be defined. But these are no longer independent of each other. In this way, every swap of the places and to swaps with the first place can be traced back:
Injective and projective tensor product
If the vector spaces that you want to tensor with each other have a topology , then it is desirable that their tensor product also has a topology. There are of course many ways of defining such a topology. However, the injective and the projective tensor product are a natural choice.
Tensor analysis
Originally, the tensor calculus was not studied in the modern algebraic concept presented here. The tensor calculus arose from considerations on differential geometry. In particular, Gregorio Ricci-Curbastro and his student Tullio Levi-Civita who developed it. The tensor calculus is therefore also called the Ricci calculus. Albert Einstein took up this calculation in his theory of relativity , which earned him great fame in the professional world. The tensors of that time are now called tensor fields and still play an important role in differential geometry today. In contrast to tensors, tensor fields are differentiable mappings that assign a tensor to each point of the underlying (often curved) space.
See also
literature
- Theodor Bröcker : Linear Algebra and Analytical Geometry. Birkhäuser, Basel 2004, ISBN 3-7643-2178-4 , chap. VII: Tensor calculus.
- Ralph Abraham , Jerrold E. Marsden , T. Ratiu: Manifolds, tensor analysis, and applications (= Applied mathematical sciences. 75). 2nd Edition. Springer, New York NY a. a. 1998, ISBN 0-387-96790-7 .
- Theodore Frankel : The Geometry of Physics. An Introduction. Cambridge University Press, Cambridge u. a. 1997, ISBN 0-521-38334-X .
- Horst Teichmann : Physical applications of vector and tensor calculations (= BI university pocket books . 39). 3. Edition. Bibliographisches Institut , Mannheim u. a. 1973, ISBN 3-411-00039-2 .
- André Lichnerowicz : Introduction to tensor analysis (= BI university pocket book. 77). Bibliographisches Institut, Mannheim u. a. 1966.
- Horst Lippmann : Applied tensor calculus. Springer 1993.
- Mikhail Itskov: Tensor algebra and tensor analysis for engineers. 3. Edition. Springer, Heidelberg a. a. 2013, ISBN 978-3-642-30878-9 .
- Adalbert Duschk : The concept of tensor and its meaning for physics. Part 1, 2, 3, Physikalische Blätter 1954, 1955, Part 1, Geometric Basics, Part 2, Tensalgebra, Part 3, Tensoranalysis.
- Karin Reich : The development of the tensor calculus. From the absolute differential calculus to the theory of relativity. Birkhäuser 1994 (on the history).
Web links
- Georg Bernhardt: About tensors, matrices and pseudovectors. PDF, German, 340 kB.
- Joseph C. Kolecki: An Introduction to Tensors for Students of Physics and Engineering. Introduction to tensor calculus for students, PDF, English, 328 kB, NASA publication.
- Eigenvalue-Eigenvector Glyphs: Visualizing Zeroth, Second, Fourth and Higher Order Tensors in a Continuum. Website for the visualization of vectors, English.
- Siegfried Petry: Introduction to tensor calculus.
Individual evidence
- ↑ MMG Ricci, T. Levi-Civita: Méthodes de calcul différentiel absolu et leurs applications. In: Mathematical Annals. 54, 1901, ISSN 0025-5831 , pp. 125-201, online.
- ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , pp. 172-179.
- ^ R. Abraham, Jerrold E. Marsden , T. Ratiu: Manifolds, tensor analysis, and applications (= Applied mathematical sciences 75). 2nd Edition. Springer, New York NY et al. 1988, ISBN 0-387-96790-7 pp. 338-339.
- ^ Kerstin Weinberg: Lecture notes. Tensalgebra and Analysis. (PDF; 235 kB) University of Siegen , October 24, 2012, accessed on July 19, 2013 .
- ^ Heinz Schade, Klaus Neemann: Tensoranalysis . 2nd revised edition. de Gruyter, Berlin / New York 2006, ISBN 3-11-018943-7 , pp. 277 ff .