This article describes the stress tensor in continuum mechanics. For Maxwell's stress tensor see
energy-momentum tensor .
A stress tensor is a second order tensor that describes the state of stress at a certain point within matter. It is an essential quantity of continuum mechanics , in which it occurs in the formulation of physical laws . A force is transmitted through a material bond of bodies through a stress tensor field that fills it and represents the flow of force in the body. The performance of the stress tensor at strain velocities contributes to the energy balance .
The stress tensor combines the normal stresses in the normal direction as well as tangentially acting (transversal) shear stresses into a mathematical object. The components of the stress tensor have the dimension ML −1 T −2, i.e. force per area , for which the units megapascal (MPa) and Newton per square millimeter (N / mm²) are common in solid mechanics . The stress tensor was introduced by Augustin-Louis Cauchy .
This tensor is mainly used in physics ( solid state physics , fluid mechanics and classical mechanics , partly geophysics ) and in electrodynamics .
definition
Stress tensors can be divided into two groups:
- Stress tensors that are used in the momentum balance and
- Stress tensors used in material theory.
The Cauchy stress tensor belongs to both groups and is the most widely used measure of stress. It is often simply called a stress tensor without adding a name. The stress tensors can all be converted into one another anytime and anywhere, which is why all stress tensors are physically equally relevant. They are just more or less practical to use in different contexts. The symbols for the stress tensors are not uniform in the literature. In the case of small distortions , there is no need to distinguish between these stress tensors. The stress tensors are objective , reference system-invariant tensors, i. H. two different observers perceive the stress tensors always in the same way.

Stress tensors that are used in the momentum balance
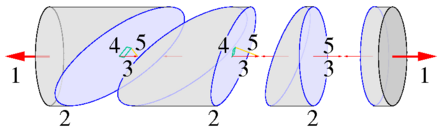
In an imaginary intersection through matter, the material that has been cut away in thought, following the principle of intersection , exerts a tension on the remaining matter, which is a Cauchy stress vector (also called traction vector ) from a normal stress component ( acting at right angles to the intersection) and two shear stress components (in the cut surface), which depend on the orientation of the surface, see pictures.




Components of the stress tensor
σ ij on a cut cube. The first index refers to the normal direction of the surface and the second index to the effective direction of the stress.
At the respective location, three such imaginary intersections intersect with the basic unit vectors of the coordinate system as normals, see the cut-out cube in the picture. The three stress vectors in the three sectional areas completely define the stress state there and are summarized line by line to form the stress tensor:


The dyadic product denotes (tensor product of two vectors). The choice of the coordinate system is irrelevant because as a tensor, the stress tensor is independent of coordinates. With the stress tensor defined in this way, the stress vector at an infinitesimal intersection with the normal vector is calculated according to:



The transposition "(·) T " is due to the meaning of the component indices. In honor of its author, this tensor is also called Cauchy's stress tensor, which is composed of the “true” or “current” stresses. It is symmetrical due to the second Cauchy-Euler law of motion ( angular momentum balance ) and is used in Euler's approach .
When converting the stress vectors from the spatial Euler to the material Lagrange representation , the change in the surface elements must be taken into account. Here F is the deformation gradient , F T − 1 the inverse of its transpose and det ( F ) its determinant . The normal unit vectors and are defined in the same way as the differentials d a and d A in the spatial or material representation. A "surface force element" thus reads:




Therein is N the Nennspannungstensor ( English nominal stress ) which represents the voltages based on the output face, and P is the first Piola-Kirchhoff stress tensor. These two tensors are generally unsymmetrical, but the products F · N and P · F T must be symmetric, see #Therial momentum balance or Cauchy-Euler's second law of motion
Further stress tensors used in material theory
The stress tensor is a tensor field that is defined at every material or spatial point within a body. The first material view corresponds to the Lagrange representation and the latter spatial to the Euler representation . Both approaches define several stress tensors:
- The spatial Cauchy stress tensor

- The spatially weighted Cauchy's or Kirchhoff's stress tensor , which is used in metal plasticity, where the plastic incompressibility J is kept constant,

- The material second Piola - Kirchhoff stress tensor , which is used, for example, for Cauchy elasticity ,

- The material convective stress tensor

-
Viscous stress tensor in flowing media
Here F is the deformation gradient , F −1 its inverse , F T − 1 the inverse of the transpose and J = det ( F ) its determinant . These stress tensors are symmetrical due to the angular momentum balance. The use of these tensors is presented in the section #energy balance .
Conversion of the stress tensors into one another
The table summarizes the conversion of the tensors.
|
 |
 |

|
 |
 |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Here F is the deformation gradient , F −1 its inverse , F T − 1 its transposed inverse, J = det ( F ) its determinant and C = F T · F the right Cauchy-Green tensor .
Spellings
In matrix notation, a stress tensor is given in the following common forms:

Sometimes, as in the left matrix notation, the index of the normal stress component is only simply noted (as in σ x = σ xx ), because it has the same normal and effective direction. However, it must be ensured that it cannot be confused with the principal stresses ( σ 1,2,3 or σ I, II, III ).
The symmetrical stress tensors, especially Cauchy's stress tensor, do not consist of nine independent quantities, but only six and can be written in Voigt's notation as a 6 × 1 vector, which significantly simplifies the notation:

Properties of the symmetric stress tensors
For matrices as well as for stress tensors, eigenvalues σ i and eigenvectors are important that solve the eigenvalue problem

to solve. The eigenvalues are invariant in the reference system, but there are other invariants (which can be derived from the three eigenvalues) that are suitable for assessing the state of stress.
In the symmetrical stress tensors, the eigenvalues are all real and the eigenvectors are perpendicular or orthogonal in pairs.
Principal stresses and maximum cutting stresses
The eigenvalues are called principal stresses and the eigenvectors (normalized to length one and therefore written with a hat) are called principal stress directions, see principal stress and principal stress direction . In the main stress directions there are only normal stresses and no shear stresses.
The eigenvalues result from the characteristic equation

where are the coefficients for the main invariants
![{\ displaystyle {\ begin {aligned} \ operatorname {I} _ {1} ({\ varvec {\ sigma}}) = & \ operatorname {Sp} ({\ varvec {\ sigma}}) = \ sigma _ { xx} + \ sigma _ {yy} + \ sigma _ {zz} \\ [1ex] \ operatorname {I} _ {2} ({\ varvec {\ sigma}}) = & {\ frac {1} {2 }} [\ operatorname {I} _ {1} {({\ varvec {\ sigma}})} ^ {2} - \ operatorname {I} _ {1} ({\ varvec {\ sigma}} ^ {2 })] = \ sigma _ {xx} \ sigma _ {yy} + \ sigma _ {xx} \ sigma _ {zz} + \ sigma _ {yy} \ sigma _ {zz} - \ sigma _ {xy} ^ {2} - \ sigma _ {xz} ^ {2} - \ sigma _ {yz} ^ {2} \\ [1ex] \ operatorname {I} _ {3} ({\ boldsymbol {\ sigma}}) = & \ operatorname {det} ({\ boldsymbol {\ sigma}}) = \ sigma _ {xx} \ sigma _ {yy} \ sigma _ {zz} +2 \ sigma _ {xy} \ sigma _ {yz} \ sigma _ {xz} - \ sigma _ {xx} \ sigma _ {yz} ^ {2} - \ sigma _ {xy} ^ {2} \ sigma _ {zz} - \ sigma _ {xz} ^ {2} \ sigma _ {yy} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55c6b29fac3af1ad1ed1327203494cc9810f7526)
and the components are the stress components in the Cartesian xyz system. The operator “Sp” forms the trace , “det” the determinant and 1 is the unit tensor .

The main stress directions are pairwise perpendicular to one another or orthogonalizable and thus form an orthonormal basis . In this basic system the stress tensor has a diagonal form :


The amounts of the intersection stress vectors

assume extreme values in two of the three main stress directions.

| proof
|
Because the root function grows monotonically with its argument, it is easier to search for the extreme values of the absolute squares:

In this, λ is a Lagrange multiplier for the secondary condition In the extremum is and therefore as desired . Furthermore, the directional derivative disappears  

in all directions which is why the vector in the round brackets is the zero vector and


follows. Hence is eigenvector of and these vectors agree with the eigenvectors of because of
   

|
Usually the principal stresses σ I, II, III are named so that σ I ≥ σ II ≥ σ III applies. Then in the I direction the magnitude largest and in the III direction the absolute smallest intersection stress vector lies.
Maximum shear stresses
The maximum shear stresses occur in a plane e, which is perpendicular to a principal stress direction. Of Mohr's stress circle shows that the maximum shear stress occurs at a 45 ° angle to the principal stress directions in the plane e and of amount equal to half the difference of the corresponding main voltages. This results in the maximum shear stress:

If σ I = σ III , the material point is under hydrostatic tension / pressure and there are no shear stresses in any plane.
If the 1-3-plane is the xy-plane and in it a plane stress state ( σ x , σ y , τ xy ) is given, then the maximum shear stress is

| proof
|
The maximum shear stresses can be derived by extracting the shear stresses from the stress tensor via

The base unit vectors result from rotations from base unit vectors of any orthonormal base , and the rotation is sought which makes it stationary . Rotations are represented with orthogonal tensors Q , which have the properties Q · Q T = 1 with the unit tensor 1 . So be . Then should
   

become stationary under the secondary condition Q · Q T = 1 . The colon “:” forms the Frobenius scalar product of two tensors A and B using the trace A : B : = Sp ( A T · B ). The secondary condition is taken into account in the objective function with a tensorial Lagrange multiplier L :

Stationarity occurs when the directional derivatives vanish in all directions H for both arguments of the objective function. If

H applies in all directions , then the secondary condition is necessarily fulfilled as desired. The variation of the orthogonal tensor is calculated using the properties of the scalar product
![{\ displaystyle {\ begin {aligned} \ mathrm {D} \ Pi (\ mathbf {Q | H}, \ mathbf {L}) = & (\ mathbf {H} ^ {\ top} \ cdot {\ boldsymbol { \ sigma}} \ cdot \ mathbf {Q}): ({\ hat {e}} _ {x} \ otimes {\ hat {e}} _ {y}) + (\ mathbf {Q} ^ {\ top } \ cdot {\ boldsymbol {\ sigma}} \ cdot \ mathbf {H}): ({\ hat {e}} _ {x} \ otimes {\ hat {e}} _ {y}) + \ mathbf { L}: (\ mathbf {H \ cdot Q ^ {\ top} + Q \ cdot H ^ {\ top}}) \\ = & \ {[\ underbrace {{\ boldsymbol {\ sigma}} \ cdot ({ \ hat {e}} _ {2} \ otimes {\ hat {e}} _ {1}) + {\ boldsymbol {\ sigma}} ^ {\ top} \ cdot ({\ hat {e}} _ { 1} \ otimes {\ hat {e}} _ {2})} _ {\ mathbf {A}} + \ underbrace {\ mathbf {L + L ^ {\ top}}} _ {\ mathbf {B}} ] \ cdot \ mathbf {Q} \}: \ mathbf {H} \, {\ stackrel {\ displaystyle!} {=}} \, 0 \,. \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdb7cad6f765a857d6bd3bf6e3f2db8c678fb47a)
Because H is arbitrary and Q has full rank, the tensor in the square brackets vanishes, and because tensor B is symmetric , tensor A is too. In the 123 system shows

So τ 13 = τ 32 = 0, σ 11 = σ 22 and with a symmetric stress tensor it follows:

This is the eigenvector of the stress tensor. Be so that Q about the z-direction rotates. Then with the angle of rotation φ , the angle functions sin and cos and their double angle functions are calculated :
 

The tangent of the double angle of rotation results from the last condition and the double angle functions

from which the maximum shear stress is finally determined with the mutual representations of the angle functions

The last form with the principal stresses σ I, II results from

in the plane stress state.
|
Invariants
If the stress tensor is changed when the basic system is changed as in

is expressed in relation to another basic system , then its components change from to in a characteristic way, just as the components of a geometric vector change when the basic system is changed. However, the amount of the vector does not change and the stress tensor also has so-called invariants that do not change when the base is changed. Such invariant or objective quantities are of interest in material theory, because any material behaves in a system-invariant manner. Are invariant:



- the main invariants

- the main stresses

- the traces of the potencies

- the amount

- the invariants of the stress deviator and
![{\ displaystyle {\ begin {aligned} J_ {2}: = & - \ operatorname {I} _ {2} ({\ boldsymbol {\ sigma}} ^ {\ mathrm {D}}) = {\ frac {1 } {3}} \ operatorname {I} _ {1} ^ {2} ({\ boldsymbol {\ sigma}}) - \ operatorname {I} _ {2} ({\ boldsymbol {\ sigma}}) = { \ frac {1} {6}} {[(\ sigma _ {I} - \ sigma _ {II}) ^ {2} + (\ sigma _ {II} - \ sigma _ {III}) ^ {2} + (\ sigma _ {III} - \ sigma _ {I}) ^ {2}]}, \\ J_ {3}: = & \ operatorname {I} _ {3} ({\ boldsymbol {\ sigma}} ^ {\ mathrm {D}}) = \ operatorname {I} _ {3} ({\ boldsymbol {\ sigma}}) - {\ frac {1} {3}} \ operatorname {I} _ {1} ( {\ boldsymbol {\ sigma}}) \ cdot \ operatorname {I} _ {2} ({\ boldsymbol {\ sigma}}) + {\ frac {2} {27}} \ operatorname {I} _ {1} ^ {3} ({\ boldsymbol {\ sigma}}) = (\ sigma _ {I} - \ sigma _ {m}) (\ sigma _ {II} - \ sigma _ {m}) (\ sigma _ { III} - \ sigma _ {m}), \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad08dfe080206ceaa607caf60291102fc1441b31)
- the Haigh – Westergaard coordinates

see section Eigensystem . This contains the stress deviator , the mean normal stress and the lode angle . The colon “:” forms the Frobenius scalar product of two tensors A and B using the trace A : B : = Sp ( A T · B ). Of these invariants, however, only three are independent of one another and all others can then be derived from them. In particular, according to Vieta's theorem :



![{\ displaystyle {\ begin {array} {l} \ operatorname {I} _ {1} ({\ boldsymbol {\ sigma}}) = \ sigma _ {I} + \ sigma _ {II} + \ sigma _ { III} \\ [1ex] \ operatorname {I} _ {2} ({\ boldsymbol {\ sigma}}) = \ sigma _ {I} \ sigma _ {II} + \ sigma _ {II} \ sigma _ { III} + \ sigma _ {III} \ sigma _ {I} \\ [1ex] \ operatorname {I} _ {3} ({\ boldsymbol {\ sigma}}) = \ sigma _ {I} \ sigma _ { II} \ sigma _ {III} \,. \ End {array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8ad99ce4eb55272ec5583b340fcbe6be0446259)
The von Mises equivalent stress

is a function of the second main invariant of the stress deviator, which is why it does not react to hydrostatic stresses (normal stresses of the same size in all three spatial directions).
Connection with other quantities
The Cauchy stress tensor contains the “true” or “current” stresses in the deformed body (in the current configuration). These tensions are related to the pressure in the body, the force acting on it and its deformations.
Maxwell's stress tensor from electrodynamics is a sub-matrix of the energy-momentum tensor .
pressure
The pressure in a material is the negative mean value of the normal stresses

and because the trace is an invariant, the pressure is frame of reference invariant. The symbols σ m and σ H are still used for the mean normal stress . The spherical part of the stress tensor is called the pressure tensor:

According to the product rule, the following applies to the divergence of the pressure tensor :

Grad forms the gradient in this .
The pressure and the pressure tensor are particularly important with liquids and gases.
In the case of liquids, there is often (to a good approximation) incompressibility . Here the pressure is a “ constrained tension ” that maintains incompressibility as a reaction of the liquid to attempts to compress it. Mathematically, the pressure here is a Lagrangeian multiplier for the secondary condition “incompressibility.” Incompressibility also occurs in solids, where the pressure then plays the same role as in incompressible fluids. With solids, negative pressure can also occur.
force
In reality and in continuum mechanics, forces that act on a body are always introduced over an area, i.e. H. on a part a σ of the surface a with a normal vector , stress vectors act on the body:



With the agreement that zero stress vectors act on the rest of the surface ( on a \ a σ ), and if the surface is sufficiently smooth, this relationship can be transformed with the divergence theorem:


Here v is the volume of the body and div is the divergence operator .
Eine von außen einwirkende Kraft induziert im Körper ein Spannungstensorfeld, das den ganzen Körper ausfüllt.
This fact initially has nothing to do with the properties of the body: The tensor field exists in rigid bodies , solids, liquids and gases, provided that they are modeled as a continuum . According to the above equation, the divergence of the stress tensor can be viewed as a “specific force” (force per volume) in order to underline that the stress tensor at the material point is an impressed influence.
The force will deform the body and / or set it in motion, which has an effect on the tensions but also on the force itself, see also the section #Calculating the tensions below.
Strain tensor
A with forces loaded with voltages stressed body is set in motion and / or deformed, see #Berechnung the voltages below. Both depend on the material properties, the former primarily on the density . With regard to material properties, a distinction must be made between two groups of materials: the liquids and gases , which are collectively referred to as fluids , and the solids .
Fluids are characterized, among other things, by the fact that they are isotropic and cannot transfer any shear stress in mechanical equilibrium . In equilibrium, the stress tensor is therefore a pressure tensor, see above. In equilibrium, solids are able to withstand shear stresses as well as unixial and biaxial tension / pressure . In the case of solids, the stress tensor can therefore be fully occupied in equilibrium.
In the model concept of continuum mechanics, materials generate a reaction stress when deformed, which counteracts the deformation. The tension introduced from the outside as a result of a load is transmitted by the material and must be in equilibrium with the reaction tension brought by the material at all times and everywhere. The material theory deals with the relationship between the stress tensor and the deformation associated with the Green-Lagrangian strain tensor E is measured. The most general material model of a simple material , which by definition is deterministic, local and objective, is:

There is a tensor-valued functional , t the time, τ a time parameter and a material point. The explicit dependence of the functional on the material point is due to material properties that may vary in location and time. The index τ ≤ t symbolizes that the entire past history of the material point and the distortions that have occurred in it can enter into the value of the functional, as is the case, for example, with the hot forming of a metal .


Physical context
This section deals with the use of the stress tensor in physical laws and engineering.
Momentum balance
A force that acts on a real body and can be expressed with the stress tensor, as shown above, will set the body in motion according to the law “ force equals mass times acceleration ”. This law is also called the momentum balance.
If an (infinitesimal) small partial body is cut free from a body and its surface is allowed to approach zero, it follows from the momentum balance that the relationship between the normal vector to a cutting surface and the cutting stress vector must be linear, since the stress state is homogeneous if the considered area approaches zero, since stress states are usually continuous . This is the statement of Cauchy's fundamental theorem with which Augustin-Louis Cauchy introduced the stress tensor as a linear operator between the normal vectors and the intersectional stress vectors.
The volume of an (infinitesimal) small body approaches zero faster than its surface, which is why mass effects could be neglected in the above consideration. If the volume of the part of the body now approaches zero, then the first Cauchy-Euler law of motion follows .
Cauchy's fundamental theorem
If an (infinitesimal) small tetrahedron with edge length L is cut out of a loaded body, then the material that has been cut away in thought exerts tensions on each cut surface, which accelerate the tetrahedron via its attack surface according to the law “ force equals mass times acceleration ”. Because the mass of a decreasing tetrahedron approaches zero with L³ , but its surface only with L² , mass effects can be neglected with L → 0 and the area-distributed forces must be in equilibrium . This is precisely the case when the relationship between the normal vectors and the intersectional stress vectors is linear:

In it is
-
 the intersection stress vector at a surface with a normal vector ,
the intersection stress vector at a surface with a normal vector ,
-
 a factor, normal vectors and a normal unit vector,
a factor, normal vectors and a normal unit vector,

-
 the stress tensor, its transpose ,
the stress tensor, its transpose ,
-
 are the components of the stress tensor, those of the stress vector and those of the normal unit vector with respect to a Cartesian coordinate system and
are the components of the stress tensor, those of the stress vector and those of the normal unit vector with respect to a Cartesian coordinate system and

- “·” Is the scalar product of vectors.
That is the statement of Cauchy's fundamental theorem. The use of a tensor ensures that the above relationships are independent of coordinates.
In the three-dimensional representation this concerns the Cauchy's stress tensor and in the material representation the nominal stress tensor.
First Cauchy-Euler law of motion

Intersectional
stresses σ ij on a cut-free cube.
A cuboid cut free in a body that is subject to an acceleration due to gravity is viewed , see picture. The cutting stresses on cutting planes with normals in the positive coordinate direction are on the positive cutting edge and the cutting stresses on cutting planes with normals in negative coordinate direction are on the negative cutting edge and act in the opposite direction to the former. There is an (infinitesimal) small distance between the positive and negative cutting edge over which the cutting stresses can change. In the case of an (infinitesimal) small cuboid, the sectional stresses can be assumed to be constant over the area of the cuboid, the density, the acceleration and the acceleration due to gravity as constant over the volume. Balancing the forces on the cuboid with edge lengths d x 1 , d x 2 and d x 3 in 1, 2 or 3-direction provides according to the law " force equals mass times acceleration " in i-direction

![{\ displaystyle {\ begin {aligned} \ rho {\ ddot {x}} _ {i} \, \ mathrm {d} x_ {1} \ mathrm {d} x_ {2} \ mathrm {d} x_ {3 } = & [\ sigma _ {1i} (x_ {1} + \ mathrm {d} x_ {1}, x_ {2}, x_ {3}) - \ sigma _ {1i} (x_ {1}, x_ {2}, x_ {3})] \, \ mathrm {d} x_ {2} \ mathrm {d} x_ {3} \\ & + [\ sigma _ {2i} (x_ {1}, x_ {2 } + \ mathrm {d} x_ {2}, x_ {3}) - \ sigma _ {2i} (x_ {1}, x_ {2}, x_ {3})] \, \ mathrm {d} x_ { 1} \ mathrm {d} x_ {3} \\ & + [\ sigma _ {3i} (x_ {1}, x_ {2}, x_ {3} + \ mathrm {d} x_ {3}) - \ sigma _ {3i} (x_ {1}, x_ {2}, x_ {3})] \, \ mathrm {d} x_ {1} \ mathrm {d} x_ {2} \\ & + \ rho k_ { i} \, \ mathrm {d} x_ {1} \ mathrm {d} x_ {2} \ mathrm {d} x_ {3} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16a767b119a70249aab92fc6e8120d90e3a55d77)
for i = 1,2,3. This is the acceleration and the gravitational acceleration in the i-direction and ρ is the density of the cuboid. Division by the volume d x 1 d x 2 d x 3 leads to d x 1,2,3 → 0
in the limit range


This is the ith component of the vector equation

in a Cartesian coordinate system as in the picture. This vector equation is the first Cauchy-Euler law of motion , which is the local form of the momentum balance , which, if it is fulfilled at every point of a body , ensures that the movement of the body as a whole - including deformations - obeys the momentum balance.
The derivation here is based on small shifts. See the main article for the effects of large displacements.
Angular momentum balance or Cauchy-Euler's second law of motion
The second Cauchy-Euler law of motion is the application of the twist law to a continuum . External torques change the body's angular momentum. The portion that affects the orbital angular momentum of its particles does not apply due to the momentum balance. What remains is an ineffective moment contribution, which is made by shear stresses between the particles, and for this contribution to disappear, the Cauchy stress tensor must be symmetrical in the spatial and the second Piola-Kichhoff stress tensor in the material perspective:

This is the second Cauchy-Euler law of motion in spatial and material formulation, which is the local form of the angular momentum balance which, if it is fulfilled together with the first Cauchy-Euler law of motion at every point in a body , ensures that the Movement of the body as a whole - including deformations - obeys the angular momentum balance.
Energy balance
The stress tensors used in material theory occur in the physical laws in combination with distortion measures, such as in the principle of d'Alembert or in the energy balance . The latter will be treated as an example.
So that the specific voltage power contributing to the energy balance is reference system invariant, the objective time derivatives are used in the spatial formulation

are required, which are formed with the velocity gradient l = Ḟ · F −1 . The superpoint denotes the material time derivative , just as it does below . With the strain tensors


the objective distortion speeds are calculated

and the specific voltage power

Here, ρ 0 = ρ det ( F ) is the density of the material, ρ is the density in the deformed body and the colon ":" forms the Frobenius scalar product of two tensors A and B using A : B : = Sp ( A T · B ) . The incremental voltage output is also physically relevant

and the "supplementary service"

In parentheses are the working terms

from stress to strain.
Calculation of the stresses
When designing components, for safety reasons, it is often necessary to provide evidence that the stresses do not exceed certain limits. Relevant here are the von Mises equivalent stress defined above and the maximum shear stress for which the complete stress state or stress tensor is to be submitted. The physical laws do not make any statements about the material behavior and are therefore not sufficient for determining the stress tensor.
In general, the movement and the state of stress result from a non-linear interplay of bearing, applied load, component and material properties. The reaction forces in the bearings and other loads induce a stress tensor field that is linked via a material model to a strain tensor field , which in turn results from movement components that are sufficient for the bearings. The system of equations
- Momentum balance and possibly other physical laws,
- kinematic equations (bearings and state of distortion) as well as
- constitutive equations (relation between stresses and strains)
is completed and leads to the basic predictability of the state of tension and movement.
Examples
Tensile test
If a straight prismatic rod is pulled uniaxially in the x-direction, the stress tensor reads

In static equilibrium and in the absence of a volume-distributed force, the momentum balance provides the condition

In static equilibrium, the normal stress σ is therefore constant in the x direction. The side surfaces of the rod are free of tension because of .

Bend of the straight beam
When the straight beam is bent in the xz plane, the stress tensor reads

In static equilibrium and in the absence of a volume-distributed force, the momentum balance provides the condition

So here, too, σ must be constant in the x-direction and the side surfaces of the beam can be considered to be free of stress to a good approximation due to small displacements . See also the example under the compatibility conditions .

torsion

Torsion of a round bar with shear distortion γ and shear stress
τ and a horizontal z-axis.
In the case of the torsion of the straight circular cylinder around its figure axis , which lies in cylinder coordinates (r, φ , z) in the direction of the z-axis, the stress tensor reads

with a shear stress τ . In static equilibrium and in the absence of a volume-distributed force, the momentum balance provides the condition
![{\ displaystyle {\ begin {aligned} \ operatorname {div} ({\ boldsymbol {\ sigma}}) = & \ left [\ sigma _ {rr, r} + {\ frac {1} {r}} (\ sigma _ {\ varphi r, \ varphi} + \ sigma _ {rr} - \ sigma _ {\ varphi \ varphi}) + \ sigma _ {zr, z} \ right] {\ hat {e}} _ {r } \\ & + \ left [\ sigma _ {r \ varphi, r} + {\ frac {1} {r}} (\ sigma _ {\ varphi \ varphi, \ varphi} + \ sigma _ {r \ varphi } + \ sigma _ {\ varphi r}) + \ sigma _ {z \ varphi, z} \ right] {\ hat {e}} _ {\ varphi} \\ & + \ left [\ sigma _ {rz, r} + {\ frac {1} {r}} (\ sigma _ {\ varphi z, \ varphi} + \ sigma _ {rz}) + \ sigma _ {zz, z} \ right] {\ hat {e }} _ {z} \\ = & {\ frac {\ partial \ sigma _ {z \ varphi}} {\ partial z}} {\ hat {e}} _ {\ varphi} + {\ frac {1} {r}} {\ frac {\ partial \ sigma _ {\ varphi z}} {\ partial \ varphi}} {\ hat {e}} _ {z} = {\ frac {\ partial \ tau} {\ partial z}} {\ hat {e}} _ {\ varphi} + {\ frac {1} {r}} {\ frac {\ partial \ tau} {\ partial \ varphi}} {\ hat {e}} _ {z} = {\ vec {0}}, \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/994e2ba5354815c308c12825f46485bb834275ed)
which is fulfilled when τ is constant in the z and φ directions. A coordinate after a comma in the index means here a derivative according to the coordinate as in

The outer surface of the cylinder is free of tension because of .

Eigensystem
The Cauchy stress tensor has the form

Its characteristic equation is

which the solutions

owns. With the approach

you get

with the solution and the consequence


One determines accordingly

The eigenvectors are pairwise perpendicular to each other. In the basic system of eigenvectors the stress tensor has a diagonal form:

which confirms the invariance of its trace.
See also
Individual evidence
-
^ Name after Haupt (2010), based on C. Truesdell: The non-linear field theories of mechanics . In: S. Flügge (Ed.): Handbuch der Physik . tape III / 3 . Springer, 2013, ISBN 978-3-642-46017-3 . refers.
-
↑ NS Ottosen, M. Ristinmaa: The Mechanics of Constitutive Modeling . Elsevier, Amsterdam 2005, ISBN 0-08-044606-X , pp. 149 f . ( google.de [accessed on January 14, 2017]).
-
↑ Brandt, Dahmen: Mechanics: An introduction to experiment and theory . Springer, 2004, p. 326 ( springer.com ).
-
↑ Haupt (2010), p. 283
-
↑ In Haupt (2010) is A Haupt = e Wikipedia , e Haupt = - A Wikipedia and a Haupt = - a Wikipedia
literature
- Holm Altenbach: Continuum Mechanics. Introduction to the material-independent and material-dependent equations . 2nd Edition. Springer Vieweg, Berlin et al. 2012, ISBN 978-3-642-24118-5 .
- P. Haupt: Continuum Mechanics and Theory of Materials . Springer, 2010, ISBN 978-3-642-07718-0 .































































![{\ displaystyle {\ begin {aligned} \ operatorname {I} _ {1} ({\ varvec {\ sigma}}) = & \ operatorname {Sp} ({\ varvec {\ sigma}}) = \ sigma _ { xx} + \ sigma _ {yy} + \ sigma _ {zz} \\ [1ex] \ operatorname {I} _ {2} ({\ varvec {\ sigma}}) = & {\ frac {1} {2 }} [\ operatorname {I} _ {1} {({\ varvec {\ sigma}})} ^ {2} - \ operatorname {I} _ {1} ({\ varvec {\ sigma}} ^ {2 })] = \ sigma _ {xx} \ sigma _ {yy} + \ sigma _ {xx} \ sigma _ {zz} + \ sigma _ {yy} \ sigma _ {zz} - \ sigma _ {xy} ^ {2} - \ sigma _ {xz} ^ {2} - \ sigma _ {yz} ^ {2} \\ [1ex] \ operatorname {I} _ {3} ({\ boldsymbol {\ sigma}}) = & \ operatorname {det} ({\ boldsymbol {\ sigma}}) = \ sigma _ {xx} \ sigma _ {yy} \ sigma _ {zz} +2 \ sigma _ {xy} \ sigma _ {yz} \ sigma _ {xz} - \ sigma _ {xx} \ sigma _ {yz} ^ {2} - \ sigma _ {xy} ^ {2} \ sigma _ {zz} - \ sigma _ {xz} ^ {2} \ sigma _ {yy} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55c6b29fac3af1ad1ed1327203494cc9810f7526)






















![{\ displaystyle {\ begin {aligned} \ mathrm {D} \ Pi (\ mathbf {Q | H}, \ mathbf {L}) = & (\ mathbf {H} ^ {\ top} \ cdot {\ boldsymbol { \ sigma}} \ cdot \ mathbf {Q}): ({\ hat {e}} _ {x} \ otimes {\ hat {e}} _ {y}) + (\ mathbf {Q} ^ {\ top } \ cdot {\ boldsymbol {\ sigma}} \ cdot \ mathbf {H}): ({\ hat {e}} _ {x} \ otimes {\ hat {e}} _ {y}) + \ mathbf { L}: (\ mathbf {H \ cdot Q ^ {\ top} + Q \ cdot H ^ {\ top}}) \\ = & \ {[\ underbrace {{\ boldsymbol {\ sigma}} \ cdot ({ \ hat {e}} _ {2} \ otimes {\ hat {e}} _ {1}) + {\ boldsymbol {\ sigma}} ^ {\ top} \ cdot ({\ hat {e}} _ { 1} \ otimes {\ hat {e}} _ {2})} _ {\ mathbf {A}} + \ underbrace {\ mathbf {L + L ^ {\ top}}} _ {\ mathbf {B}} ] \ cdot \ mathbf {Q} \}: \ mathbf {H} \, {\ stackrel {\ displaystyle!} {=}} \, 0 \,. \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdb7cad6f765a857d6bd3bf6e3f2db8c678fb47a)
















![{\ displaystyle {\ begin {aligned} J_ {2}: = & - \ operatorname {I} _ {2} ({\ boldsymbol {\ sigma}} ^ {\ mathrm {D}}) = {\ frac {1 } {3}} \ operatorname {I} _ {1} ^ {2} ({\ boldsymbol {\ sigma}}) - \ operatorname {I} _ {2} ({\ boldsymbol {\ sigma}}) = { \ frac {1} {6}} {[(\ sigma _ {I} - \ sigma _ {II}) ^ {2} + (\ sigma _ {II} - \ sigma _ {III}) ^ {2} + (\ sigma _ {III} - \ sigma _ {I}) ^ {2}]}, \\ J_ {3}: = & \ operatorname {I} _ {3} ({\ boldsymbol {\ sigma}} ^ {\ mathrm {D}}) = \ operatorname {I} _ {3} ({\ boldsymbol {\ sigma}}) - {\ frac {1} {3}} \ operatorname {I} _ {1} ( {\ boldsymbol {\ sigma}}) \ cdot \ operatorname {I} _ {2} ({\ boldsymbol {\ sigma}}) + {\ frac {2} {27}} \ operatorname {I} _ {1} ^ {3} ({\ boldsymbol {\ sigma}}) = (\ sigma _ {I} - \ sigma _ {m}) (\ sigma _ {II} - \ sigma _ {m}) (\ sigma _ { III} - \ sigma _ {m}), \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad08dfe080206ceaa607caf60291102fc1441b31)




![{\ displaystyle {\ begin {array} {l} \ operatorname {I} _ {1} ({\ boldsymbol {\ sigma}}) = \ sigma _ {I} + \ sigma _ {II} + \ sigma _ { III} \\ [1ex] \ operatorname {I} _ {2} ({\ boldsymbol {\ sigma}}) = \ sigma _ {I} \ sigma _ {II} + \ sigma _ {II} \ sigma _ { III} + \ sigma _ {III} \ sigma _ {I} \\ [1ex] \ operatorname {I} _ {3} ({\ boldsymbol {\ sigma}}) = \ sigma _ {I} \ sigma _ { II} \ sigma _ {III} \,. \ End {array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8ad99ce4eb55272ec5583b340fcbe6be0446259)




















![{\ displaystyle {\ begin {aligned} \ rho {\ ddot {x}} _ {i} \, \ mathrm {d} x_ {1} \ mathrm {d} x_ {2} \ mathrm {d} x_ {3 } = & [\ sigma _ {1i} (x_ {1} + \ mathrm {d} x_ {1}, x_ {2}, x_ {3}) - \ sigma _ {1i} (x_ {1}, x_ {2}, x_ {3})] \, \ mathrm {d} x_ {2} \ mathrm {d} x_ {3} \\ & + [\ sigma _ {2i} (x_ {1}, x_ {2 } + \ mathrm {d} x_ {2}, x_ {3}) - \ sigma _ {2i} (x_ {1}, x_ {2}, x_ {3})] \, \ mathrm {d} x_ { 1} \ mathrm {d} x_ {3} \\ & + [\ sigma _ {3i} (x_ {1}, x_ {2}, x_ {3} + \ mathrm {d} x_ {3}) - \ sigma _ {3i} (x_ {1}, x_ {2}, x_ {3})] \, \ mathrm {d} x_ {1} \ mathrm {d} x_ {2} \\ & + \ rho k_ { i} \, \ mathrm {d} x_ {1} \ mathrm {d} x_ {2} \ mathrm {d} x_ {3} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16a767b119a70249aab92fc6e8120d90e3a55d77)




















![{\ displaystyle {\ begin {aligned} \ operatorname {div} ({\ boldsymbol {\ sigma}}) = & \ left [\ sigma _ {rr, r} + {\ frac {1} {r}} (\ sigma _ {\ varphi r, \ varphi} + \ sigma _ {rr} - \ sigma _ {\ varphi \ varphi}) + \ sigma _ {zr, z} \ right] {\ hat {e}} _ {r } \\ & + \ left [\ sigma _ {r \ varphi, r} + {\ frac {1} {r}} (\ sigma _ {\ varphi \ varphi, \ varphi} + \ sigma _ {r \ varphi } + \ sigma _ {\ varphi r}) + \ sigma _ {z \ varphi, z} \ right] {\ hat {e}} _ {\ varphi} \\ & + \ left [\ sigma _ {rz, r} + {\ frac {1} {r}} (\ sigma _ {\ varphi z, \ varphi} + \ sigma _ {rz}) + \ sigma _ {zz, z} \ right] {\ hat {e }} _ {z} \\ = & {\ frac {\ partial \ sigma _ {z \ varphi}} {\ partial z}} {\ hat {e}} _ {\ varphi} + {\ frac {1} {r}} {\ frac {\ partial \ sigma _ {\ varphi z}} {\ partial \ varphi}} {\ hat {e}} _ {z} = {\ frac {\ partial \ tau} {\ partial z}} {\ hat {e}} _ {\ varphi} + {\ frac {1} {r}} {\ frac {\ partial \ tau} {\ partial \ varphi}} {\ hat {e}} _ {z} = {\ vec {0}}, \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/994e2ba5354815c308c12825f46485bb834275ed)










