Cauchy elasticity

Cauchy elasticity (from Augustin-Louis Cauchy and from Greek ελαστικός elastikos "adaptable") is a material model of elasticity . Elasticity is the property of a body to change its shape under the action of force and to return to its original shape when the force is removed (example: spring). The cause of the elasticity are distortions of the atomic lattice (in metals), the stretching of molecular chains (rubber and plastics) or the change in the mean atomic distance (liquids and gases).

In Cauchy elasticity, the reaction forces when a body is deformed are determined exclusively by the current deformation. Such relationships describe, for example, the equations of state of gases. If the initial state is free of forces, this will be resumed after any deformation when the loads are removed. Different deformation paths that ultimately result in the same deformations result in the same reaction forces in the end. The deformation speeds also have no influence on the reactions at the material equation level. Cauchy elasticity is a time-independent material property .

Dissipative processes such as viscous or plastic flow are thus excluded, which is guaranteed with real materials within their elastic limit . Real liquids, gases and some solids (such as iron and glass) are elastic to a good approximation when there are rapid, slight changes in volume (e.g. with sound waves). In the case of solids, the elastic limit can be adhered to in the case of slow and sufficiently small deformations that are present in many applications, especially in the technical field.

Although the reaction forces in a Cauchy elastic material are not influenced by the deformation path covered, the deformation work performed on solids on different deformation paths (with the same start and end point) can vary, which in the absence of a dissipation mechanism contradicts thermodynamic principles. Path independence of the deformation work leads to hyperelasticity , which is a special case of Cauchy elasticity. Further conditions for modeling Cauchy elasticity can be derived from the principle of material objectivity, according to which the material behavior is invariant in the reference system, and in the case of isotropy .

Many elastic materials such as steel, rubber, plastic, wood and concrete, but also biological tissue, can be described to a good approximation with Cauchy elasticity.

definition

In a Cauchy elastic material, the Cauchy stress tensor is a function only of the existing deformation gradient : ${\displaystyle {\boldsymbol {\sigma }}}$ ${\displaystyle \mathbf {F} }$

${\displaystyle {\boldsymbol {\sigma }}={\mathfrak {G}}(\mathbf {F} )\,.}$

This function will generally depend on the initial state of the body, in particular the internal stresses that are initially present. In most cases, however, the undeformed ground state, in which the deformation gradient is equal to the unit tensor , will be stress-free: ${\displaystyle \mathbf {1} }$

${\displaystyle {\mathfrak {G}}(\mathbf {1} )=\mathbf {0} \,.}$

Macroscopic behavior

Force-displacement diagram in a uniaxial tensile test with non-linear elasticity

Macroscopically, the following properties can be observed on a Cauchy elastic body:

• With a given deformation (fluids: volume change) the reaction forces (the pressure) always have the same value regardless of the previous history.
• If the initial state is unloaded, it is resumed after any deformation when the loads are removed. In the case of elastic liquids and gases, the state is determined by the volume occupied, which is always the same under the same conditions.
• The material behavior is independent of the speed. The speed at which a deformation (fluids: volume change) takes place has no influence on the resistance (pressure) that the body opposes the deformation.
• In the uniaxial tensile test, loading and unloading always take place along the same path as in the adjacent picture. With liquids and gases this corresponds to a compression and expansion test.

With sufficiently small deformations, the force-displacement relationship in solids is linear and the elasticity can be described in terms of modulus. Because the force to be applied and the distance covered in the event of a deformation depend largely on the dimensions of the body, the force is related to its effective area and the distance to a suitable dimension of the body. The related force is the tension and the related distance is the elongation . The modules quantify the relationship between the stresses and the strains and are a material property. The modulus of elasticity applies to uniaxial tension, the modulus of shear to shear and the modulus of compression to all-round pressure. With uniaxial tension, a deformation occurs not only in the direction of tension, but also across it, which is recorded by the dimensionless Poisson's ratio. The complete description of the isotropic linear Cauchy elasticity only requires two of these quantities. With anisotropic linear behavior, a maximum of 36 parameters are required (only the assumption of hyperelasticity allows the reduction to 21 parameters.)

Material objectivity

The principle of material objectivity says that the material behavior is invariant of the reference system or, more precisely, is invariant to a Euclidean transformation of the reference system of an observer. The decisive factor is the rotation of the moving system relative to the body. The rotation of the frame of reference of the moving observer relative to the stationary observer is done with an orthogonal tensor from the special orthogonal group ${\displaystyle \mathbf {Q} }$

${\displaystyle {\mathcal {SO}}:=\{\mathbf {Q} \in {\mathcal {L}}|\mathbf {Q} ^{-1}=\mathbf {Q} ^{\top }\;{\text{und}}\;\det(\mathbf {Q} )=+1\}}$

described. The set contains all tensors of the second order, denotes the transposition , the inverse and “det” the determinant . The tensors from this group perform rotations without reflection. If the observer, who is at rest relative to the body, determines the deformation gradient in a material point , then the moving observer measures using the Euclidean transformation ${\displaystyle {\mathcal {L}}}$ ${\displaystyle (\cdot )^{\top }}$ ${\displaystyle (\cdot )^{-1}}$ ${\displaystyle \mathbf {F} }$

${\displaystyle \mathbf {F} '=\mathbf {Q\cdot F} \,.}$

The rotation transforms the Cauchy's stress tensor so that the observer in motion

${\displaystyle {\boldsymbol {\sigma }}'=\mathbf {Q} \cdot {\boldsymbol {\sigma }}\cdot \mathbf {Q} ^{\top }=\mathbf {Q} \cdot {\mathfrak {G}}(\mathbf {F} )\cdot \mathbf {Q} ^{\top }={\mathfrak {G}}(\mathbf {F} ')={\mathfrak {G}}(\mathbf {Q\cdot F} )}$

notices. The movement possibilities of the observer are unlimited, so that the above equation applies to all orthogonal tensors and therefore

${\displaystyle {\mathfrak {G}}(\mathbf {Q\cdot F} )=\mathbf {Q} \cdot {\mathfrak {G}}(\mathbf {F} )\cdot \mathbf {Q} ^{\top }\quad {\text{für alle}}\quad \mathbf {Q} \in {\mathcal {SO}}}$

must apply. This condition is always fulfilled in elastic fluids, while a special modeling guideline has to be followed for elastic solids.

Elastic fluids

Fluid is the collective term for liquids and gases . The elastic liquid is also known as the ideal liquid or Euler liquid, and the elastic gas is the frictionless gas. Internal friction, which would show up in viscosity and thus in shear stresses, is neglected in elastic fluids, which is why the stress tensor there has a diagonal shape. Furthermore, every fluid is also isotropic . If a fluid is now mentally cut into two parts, then cutting stresses develop on the cut surfaces that are perpendicular to the cut surface, because the pressure in an elastic fluid always acts perpendicularly on the delimiting surfaces. Now in an isotropic liquid the normal stress must be the same for all orientations of the cut surface. But this is only possible if the stress tensor is a multiple of the unit tensor :

${\displaystyle {\boldsymbol {\sigma }}={\mathfrak {G}}(\mathbf {F} )={\mathfrak {g}}(\mathbf {F} )\mathbf {1} \,.}$

The scalar function corresponds to the negative pressure , which in fluids kinematically only from the change in volume , the density ${\displaystyle {\mathfrak {g}}}$ ${\displaystyle p}$ ${\displaystyle \operatorname {det} (\mathbf {F} )}$

${\displaystyle \rho ={\frac {\rho _{0}}{\operatorname {det} (\mathbf {F} )}}}$

or the specific volume

${\displaystyle v:={\frac {1}{\rho }}={\frac {\operatorname {det} (\mathbf {F} )}{\rho _{0}}}}$

depends. The material parameter is the density in the initial state at . A stress tensor of this form ${\displaystyle \rho _{0}}$ ${\displaystyle \operatorname {det} (\mathbf {F} )=1}$

${\displaystyle {\boldsymbol {\sigma }}=-{\tilde {p}}[\operatorname {det} (\mathbf {F} )]\mathbf {1} =-p(\rho )\mathbf {1} =-{\bar {p}}(v)\mathbf {1} \,,}$

is called the pressure tensor .

Material objectivity of fluids

In fluids, the stresses are proportional to the unit tensor and only depend on the determinant of the deformation gradient, which is why the above condition for objectivity

${\displaystyle {\mathfrak {G}}(\mathbf {Q\cdot F} )=\mathbf {Q} \cdot {\mathfrak {G}}(\mathbf {F} )\cdot \mathbf {Q} ^{\top }\quad {\text{für alle}}\quad \mathbf {Q} \in {\mathcal {SO}}}$

is always fulfilled:

${\displaystyle \overbrace {{\tilde {p}}[\operatorname {det} (\mathbf {Q\cdot F} )]\mathbf {1} } ^{{\mathfrak {G}}(\mathbf {Q\cdot F} )}={\tilde {p}}[\operatorname {det} (\mathbf {Q} )\operatorname {det} (\mathbf {F} )]\mathbf {Q\cdot 1\cdot Q} ^{\top }=\mathbf {Q} \cdot \overbrace {{\tilde {p}}[\operatorname {det} (\mathbf {F} )]\mathbf {1} } ^{{\mathfrak {G}}(\mathbf {F} )}\cdot \mathbf {Q} ^{\top }\quad {\text{für alle}}\quad \mathbf {Q} \in {\mathcal {SO}}\,.}$

Material equations for elastic fluids

Many material equations for elastic fluids are called equations of state , which underlines that the pressure in them is always the same under the same conditions (temperature, volume, amount of substance), which ensures Cauchy elasticity. The density results from the volume and the amount of substance. The simplest possible connection between pressure and density is proportionality

${\displaystyle p=(R\,T)\,\rho ,}$

which defines the ideal gas in which the proportionality factor is the product of a material parameter R and the absolute temperature T. The lower the pressure and the higher the temperature, the more a real gas behaves like an ideal one.

With virial coefficients , the ideal gas equation can be ${\displaystyle B_{i}}$

${\displaystyle p=kT\sum _{i=1}^{N}B_{i}(T)\rho ^{i}}$

can be extended to describe real gases and phase transitions. The factor k is the Boltzmann constant . However, this equation is only suitable for dilute gases.

Alternatively, the pressure can also be formulated as a function of the specific volume v , such as e.g. B. in the Van der Waals equation

${\displaystyle {\bar {p}}(v)={\frac {RT}{v-b}}-{\frac {a}{v^{2}}}\;,\quad v>b}$

Materials parameters a , b and R .

Conservative fluids

A barotropic Cauchy elastic fluid is also hyperelastic because the specific tension power is due to ${\displaystyle l_{i}}$

${\displaystyle l_{i}:={\frac {1}{\rho }}{\boldsymbol {\sigma }}:\mathbf {d} =-{\frac {1}{\rho }}{\bar {p}}(v)\mathbf {1} :\mathbf {d} =-{\frac {1}{\rho }}{\bar {p}}(v)\operatorname {div} ({\vec {v}})={\bar {p}}(v){\frac {\dot {\rho }}{\rho ^{2}}}=-{\bar {p}}(v)\,{\dot {v}}=:{\dot {w}}(v)}$

the material time derivative of a scalar function w , which is only the case in hyperelastic materials. The material time derivative is indicated by the over point or D / D t below. In the chain of equations, the Frobenius scalar product “:” of the pressure tensor was used with the distortion speed tensor d  : = ½ ( l + l ^T ), which is the symmetrical part of the speed gradient . The divergence of the velocity field is equal to the trace of the velocity gradient ${\displaystyle \mathbf {l} =\operatorname {grad} ({\vec {v}})}$ ${\displaystyle {\vec {v}}}$

${\displaystyle \operatorname {div} ({\vec {v}})=\operatorname {Sp} (\mathbf {l} )=\operatorname {Sp} (\mathbf {d} )=\mathbf {1:d} \,.}$

The divergence related to the density is due to the local spatial mass balance

${\displaystyle {\dot {\rho }}+\rho \operatorname {div} ({\vec {v}})=0\quad \rightarrow \quad {\frac {1}{\rho }}\operatorname {div} ({\vec {v}})=-{\frac {\dot {\rho }}{\rho ^{2}}}={\frac {\mathrm {D} }{\mathrm {D} t}}(\rho ^{-1})={\dot {v}}}$

the material time derivative of the specific volume. This finally resulted in the specific deformation energy

${\displaystyle w(v):=-\int {\bar {p}}(v)\,\mathrm {d} v\quad \leftrightarrow \quad {\frac {\mathrm {d} w(v)}{\mathrm {d} v}}=-{\bar {p}}(v)\quad \leftrightarrow \quad {\dot {w}}(v)=-{\bar {p}}(v){\dot {v}},}$

whose material time derivative in the case of barotropy, as shown in the chain of equations above, is the specific tension power of the elastic fluid. The compression power of the pressure is converted completely and without dissipation into deformation energy in the barotropic fluid, which is why elastic barotropic fluids are invariably conservative.

Incompressible liquids

In an incompressible elastic liquid, the density is constant to a good approximation and the pressure no longer results from the constitutive equation, but from the laws of nature and the boundary conditions, but can still depend on the place and time ${\displaystyle {\vec {x}}}$ ${\displaystyle t}$

${\displaystyle {\boldsymbol {\sigma }}=-p({\vec {x}},t)\mathbf {1} \,.}$

Euler's equations in fluid mechanics

Inserting the pressure tensor into the momentum balance in Euler's version leads to Euler's equations of fluid mechanics , which, together with the continuity equation, model frictionless flows. Euler's equations are a good approximation for laminar flows when fluid dynamic boundary layers at the edges of the flow do not play an essential role.

Elastic solids

From a continuum mechanical point of view, solids differ from fluids in two main ways: firstly, they are able to withstand shear and tensile forces in equilibrium , and secondly, they can be anisotropic .

Material objectivity of elastic solids

The condition for the reference system invariance written in #Material Objectivity

${\displaystyle {\mathfrak {G}}(\mathbf {Q\cdot F} )=\mathbf {Q} \cdot {\mathfrak {G}}(\mathbf {F} )\cdot \mathbf {Q} ^{\top }\quad {\text{für alle}}\quad \mathbf {Q} \in {\mathcal {SO}}}$

is not automatically complied with for solids - in contrast to fluids - but can be ensured as follows.

The deformation gradient is polarized into an orthogonal tensor and a symmetrically positive definite right stretch tensor : ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {R} \in {\mathcal {SO}}}$ ${\displaystyle \mathbf {U} }$

${\displaystyle \mathbf {F} =\mathbf {R\cdot U} \,.}$

Now can be chosen so that because of ${\displaystyle \mathbf {Q} =\mathbf {R} ^{\top }}$ ${\displaystyle \operatorname {det} (\mathbf {F} )=\operatorname {det} (\mathbf {R} )\operatorname {det} (\mathbf {U} )=\operatorname {det} (\mathbf {U} )}$

${\displaystyle {\begin{aligned}\mathbf {R} ^{\top }\cdot {\boldsymbol {\sigma }}\cdot \mathbf {R} =&\mathbf {R} ^{\top }\cdot {\mathfrak {G}}(\mathbf {F} )\cdot \mathbf {R} ={\mathfrak {G}}(\mathbf {R^{\top }\cdot F} )={\mathfrak {G}}(\mathbf {R^{\top }\cdot R\cdot U} )={\mathfrak {G}}(\mathbf {U} )\\\rightarrow {\boldsymbol {\sigma }}=&\mathbf {R} \cdot {\mathfrak {G}}(\mathbf {U} )\cdot \mathbf {R} ^{\top }\\\rightarrow {\tilde {\mathbf {T} }}:=&\operatorname {det} (\mathbf {F} )\mathbf {F} ^{-1}\cdot {\boldsymbol {\sigma }}\cdot \mathbf {F} ^{\top -1}=\operatorname {det} (\mathbf {U} )\mathbf {U} ^{-1}\cdot {\mathfrak {G}}(\mathbf {U} )\cdot \mathbf {U} ^{\top -1}\end{aligned}}}$

results. According to the principle of material objectivity, the second Piola-Kirchhoff stress tensor in the Cauchy elasticity is exclusively a function of the current right-hand distance tensor . This condition is both necessary and sufficient for material objectivity. The material objectivity is ensured in solid models by constitutive equations in Lagrangian . It is mostly used as a function of the right Cauchy-Green tensor ${\displaystyle {\tilde {\mathbf {T} }}}$ ${\displaystyle \mathbf {U} }$ ${\displaystyle {\tilde {\mathbf {T} }}}$

${\displaystyle \mathbf {C} :=\mathbf {F^{\top }\cdot F} =\mathbf {U\cdot U} }$

or the Green-Lagrange strain tensor

${\displaystyle \mathbf {E} :={\frac {1}{2}}(\mathbf {F^{\top }\cdot F-1} )={\frac {1}{2}}(\mathbf {U\cdot U-1} )}$

modeled, for example:

${\displaystyle {\tilde {\mathbf {T} }}={\tilde {\mathfrak {G}}}(\mathbf {C} )\quad \Leftrightarrow \quad {\boldsymbol {\sigma }}={\frac {1}{\operatorname {det} (\mathbf {F} )}}\mathbf {F} \cdot {\tilde {\mathfrak {G}}}(\mathbf {C} )\cdot \mathbf {F} ^{\top }}$.

Cauchy derivative

Deriving the above equation according to the time yields with the abbreviation : ${\displaystyle J=\det(\mathbf {F} )}$

${\displaystyle {\begin{aligned}{\dot {\boldsymbol {\sigma }}}=&-{\frac {1}{J^{2}}}J(\mathbf {F} ^{\top -1}:{\dot {\mathbf {F} }})\mathbf {F} \cdot {\tilde {\mathfrak {G}}}\cdot \mathbf {F} ^{\top }+{\frac {1}{J}}{\dot {\mathbf {F} }}\cdot {\tilde {\mathfrak {G}}}\cdot \mathbf {F} ^{\top }+{\frac {1}{J}}\mathbf {F} \cdot {\dot {\tilde {\mathfrak {G}}}}\cdot \mathbf {F} ^{\top }+{\frac {1}{J}}\mathbf {F} \cdot {\tilde {\mathfrak {G}}}\cdot {\dot {\mathbf {F} }}^{\top }\\\rightarrow {\stackrel {\diamond }{\boldsymbol {\sigma }}}=&{\frac {1}{J}}\mathbf {F} \cdot {\dot {\tilde {\mathfrak {G}}}}\cdot \mathbf {F} ^{\top }\end{aligned}}}$

To the left of the last equation is the objective Cauchy derivative

${\displaystyle {\stackrel {\diamond }{\boldsymbol {\sigma }}}={\dot {\boldsymbol {\sigma }}}+\operatorname {Sp} (\mathbf {l} ){\boldsymbol {\sigma }}-\mathbf {l} \cdot {\boldsymbol {\sigma }}-{\boldsymbol {\sigma }}\cdot \mathbf {l} ^{\top }\,,}$

the one with the velocity gradient

${\displaystyle \mathbf {l} ={\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}}$

is formed.

Linear Cauchy elasticity

In the linear Cauchy-elasticity, the six independent components of strain E _ij linearly with the six independent components of the voltages linked ${\displaystyle {\tilde {T}}_{ij}}$

${\displaystyle {\begin{aligned}{\tilde {T}}_{ij}=&{\tilde {T}}_{ji}=\sum _{k,l=1}^{3}C_{ijkl}\,E_{kl}=\sum _{k,l=1}^{3}C_{ijkl}\,E_{lk}\,,\quad i,j=1,2,3\\\rightarrow C_{ijkl}=&C_{jikl}=C_{ijlk}\end{aligned}}}$

for which a maximum of 36 independent coefficients C _{ijkl are} necessary. To describe a linear Cauchy elastic material, a maximum of 36 parameters are required. Only in hyperelasticity does C _ijkl = C _{klij also apply} , so that a maximum of 21 parameters are sufficient there.

Isotropic Cauchy elasticity

Should the Cauchy stress tensor , as in isotropic hyperelasticity , function as a function of the left Cauchy-Green tensor ${\displaystyle {\boldsymbol {\sigma }}}$

${\displaystyle \mathbf {b} :=\mathbf {F\cdot F} ^{\top }}$

be expressed, therefore , the principle of material objectivity demands: ${\displaystyle {\boldsymbol {\sigma }}={\mathcal {G}}(\mathbf {b} )}$

${\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}'=&{\mathcal {G}}(\mathbf {b} ')\\\rightarrow \mathbf {Q} \cdot {\boldsymbol {\sigma }}\cdot \mathbf {Q} ^{\top }=&{\mathcal {G}}((\mathbf {Q\cdot F} )\cdot {(\mathbf {Q\cdot F} )}^{\top })={\mathcal {G}}(\mathbf {Q\cdot F\cdot F} ^{\top }\cdot \mathbf {Q} ^{\top })={\mathcal {G}}(\mathbf {Q\cdot b\cdot Q} ^{\top })\,.\end{aligned}}}$

so

${\displaystyle \mathbf {Q} \cdot {\mathcal {G}}(\mathbf {b} )\cdot \mathbf {Q} ^{\top }={\mathcal {G}}(\mathbf {Q\cdot b\cdot Q} ^{\top })\quad {\text{für alle}}\quad \mathbf {Q} \in {\mathcal {SO}}\,.}$

One function with this property is an isotropic tensor function . Such a function can be in the form ${\displaystyle {\mathcal {G}}}$

${\displaystyle {\mathcal {G}}(\mathbf {b} )=\phi _{0}{\textbf {1}}+\phi _{1}\mathbf {b} +\phi _{2}\mathbf {b\cdot b} }$

where the coefficients are scalar functions of the main invariants or other invariants of . According to Cayley-Hamilton's theorem, can be synonymous ${\displaystyle \phi _{0,1,2}}$ ${\displaystyle \mathbf {b} }$

${\displaystyle {\mathcal {G}}(\mathbf {b} )=\varphi _{0}{\textbf {1}}+\varphi _{1}\mathbf {b} +\varphi _{-1}\mathbf {b} ^{-1}}$

written with different coefficients . In any case, commute and : ${\displaystyle \varphi _{-1,0,1}}$ ${\displaystyle {\mathcal {G}}}$ ${\displaystyle \mathbf {b} }$

${\displaystyle \mathbf {b} \cdot {\mathcal {G}}(\mathbf {b} )={\mathcal {G}}(\mathbf {b} )\cdot \mathbf {b} \,.}$

In particular, is with hyperelasticity

${\displaystyle \mathbf {b} \cdot {\frac {\mathrm {d} \psi (\mathbf {b} )}{\mathrm {d} \mathbf {b} }}={\frac {\mathrm {d} \psi (\mathbf {b} )}{\mathrm {d} \mathbf {b} }}\cdot \mathbf {b} \,,}$

where the derivative of the strain energy density after is an isotropic tensor. ${\displaystyle \psi }$ ${\displaystyle \mathbf {b} }$

Navier-Cauchy equations

→ Main article : Navier-Cauchy equations

In linear isotropic elasticity, the stress tensor for small deformations is a linear isotropic tensor function of the linearized strain tensor : ${\displaystyle {\boldsymbol {\sigma }}}$ ${\displaystyle {\boldsymbol {\varepsilon }}}$

${\displaystyle {\boldsymbol {\sigma }}=\lambda \operatorname {Sp} ({\boldsymbol {\varepsilon }})\mathbf {1} +2\mu {\boldsymbol {\varepsilon }}}$

Therein are the first and second Lamé constants . This material equation is known as Hooke's law and is also hyperelastic at the same time. If the strain tensor is expressed by the displacements and inserted into the first Cauchy-Euler's law of motion , which corresponds to the local momentum balance , this leads to the Navier-Cauchy equations. ${\displaystyle \lambda ,\,\mu }$ ${\displaystyle {\vec {u}}}$

Thermodynamic consistency

→ Main article : Clausius-Duhem inequality

Even if the stresses in a Cauchy elastic material are exclusively determined by the current state of deformation, the work of deformation will generally depend on the path in which the deformation is carried out. In the absence of a dissipation mechanism, this is in contradiction to thermodynamic principles.

This is also shown by the evaluation of the Clausius-Duhem inequality, which represents the second law of thermodynamics in solid mechanics . In the case of an isothermal change of state , the Clausius-Duhem inequality reads

${\displaystyle {\frac {1}{\rho _{0}}}{\tilde {\mathbf {T} }}:{\dot {\mathbf {E} }}-{\dot {\psi }}_{0}\geq 0\,,}$

where represents the Helmholtz free energy in the Lagrangian formulation . If the free energy is a function of elongation only, which is plausible with Cauchy elasticity, then it follows ${\displaystyle \psi _{0}}$

${\displaystyle {\frac {1}{\rho _{0}}}{\tilde {\mathbf {T} }}:{\dot {\mathbf {E} }}-{\dot {\psi }}_{0}={\frac {1}{\rho _{0}}}{\tilde {\mathbf {T} }}:{\dot {\mathbf {E} }}-{\frac {\mathrm {d} \psi _{0}}{\mathrm {d} \mathbf {E} }}:{\dot {\mathbf {E} }}=\left({\frac {1}{\rho _{0}}}{\tilde {\mathbf {T} }}-{\frac {\mathrm {d} \psi _{0}}{\mathrm {d} \mathbf {E} }}\right):{\dot {\mathbf {E} }}\geq 0\,.}$

This inequality has to be fulfilled for all possible processes, which is why the term in brackets, because it does not depend on the speed of the distortion, has to disappear and therefore

${\displaystyle {\frac {1}{\rho _{0}}}{\tilde {\mathbf {T} }}={\frac {\mathrm {d} \psi _{0}}{\mathrm {d} \mathbf {E} }}}$

applies. A material with such a material equation is hyperelastic . In hyperelasticity, the work of deformation is path-independent.

A path dependency of the deformation work occurs in the following example.

example

Tensile stress in the uniaxial tensile test

The material model

${\displaystyle {\tilde {\mathbf {T} }}=G(\mathbf {C} -\mathbf {1} )+\gamma {\parallel \mathbf {C} \parallel }^{n}\ln(\operatorname {det} (\mathbf {C} ))\mathbf {C} ^{-1}}$

with material parameters and is Cauchy elastic and fulfills the criterion of material objectivity. The Frobenius norm is the trace operator calculated ${\displaystyle G,\gamma }$ ${\displaystyle n}$ ${\displaystyle \parallel \mathbf {C} \parallel }$ ${\displaystyle \operatorname {Sp} }$

${\displaystyle \parallel \mathbf {C} \parallel ={\sqrt {\operatorname {Sp} (\mathbf {C} ^{\top }\cdot \mathbf {C} )}}}$

and is an invariant of the argument . The function " " is the natural logarithm , the parameter corresponds to the shear modulus and regulates the compressibility . With is Simo and Pister's model and is hyper-elastic. Because of and one gets Cauchy's stress tensor ${\displaystyle \mathbf {C} }$ ${\displaystyle \ln }$ ${\displaystyle G}$ ${\displaystyle \gamma }$ ${\displaystyle n=0}$ ${\displaystyle \operatorname {det} (\mathbf {C} )=\operatorname {det} (\mathbf {b} )=\operatorname {det} {(\mathbf {F} )}^{2}}$ ${\displaystyle \operatorname {Sp} (\mathbf {C\cdot C} )=\operatorname {Sp} (\mathbf {b\cdot b} )}$

${\displaystyle {\boldsymbol {\sigma }}={\dfrac {1}{\operatorname {det} (\mathbf {F} )}}\mathbf {F} \cdot {\tilde {\mathbf {T} }}\cdot \mathbf {F} ^{\top }={\dfrac {G}{\sqrt {\operatorname {det} (\mathbf {b} )}}}(\mathbf {b\cdot b} -\mathbf {b} )+\gamma {\dfrac {{\parallel \mathbf {b} \parallel }^{n}\ln(\operatorname {det} (\mathbf {b} ))}{\sqrt {\operatorname {det} (\mathbf {b} )}}}\mathbf {1} }$

depending on the left stretch tensor . So the coefficients are ${\displaystyle \mathbf {b} }$ ${\displaystyle {\phi }_{0,1,2}}$

${\displaystyle {\begin{aligned}\phi _{0}=&\gamma {\dfrac {{\parallel \mathbf {b} \parallel }^{n}\ln(\operatorname {det} (\mathbf {b} ))}{\sqrt {\operatorname {det} (\mathbf {b} )}}}\\-\phi _{1}=&\phi _{2}={\dfrac {G}{\sqrt {\operatorname {det} (\mathbf {b} )}}}\,.\end{aligned}}}$

In the relaxed state is and therefore . The picture shows the course of the Cauchy stress with material parameters G = 1  megapascal and γ = 7 MPa in a uniaxial tensile test. ${\displaystyle \mathbf {b} =\mathbf {1} }$ ${\displaystyle {\boldsymbol {\sigma }}=\mathbf {0} }$

With the deformation work is path-dependent, as will now be shown. In a material point, let the deformation gradient be in the time interval ${\displaystyle n=-2}$ ${\displaystyle t\in [0,1]}$

Estimation of an integral using step functions. Red: upper limit, green: lower limit

${\displaystyle {\begin{aligned}\mathbf {F} (t,p)=&{\begin{pmatrix}1+t&0&0\\0&1+pt(1-t)&0\\0&0&1\end{pmatrix}}\\\rightarrow {\dot {\mathbf {F} }}(t,p)=&{\begin{pmatrix}1&0&0\\0&p(1-2t)&0\\0&0&0\end{pmatrix}}\end{aligned}}}$

specified with the parameter in path 1 and path 2. The two paths have the same start and end points in the specified time interval. Now you can numerically integrate the deformation power density along the two deformation paths with a step function to the deformation work density performed , see figure on the right: ${\displaystyle p=0}$ ${\displaystyle p=1}$ ${\displaystyle l}$ ${\displaystyle \psi }$

${\displaystyle {\begin{aligned}\psi (t,p)=&\rho _{0}\int _{0}^{1}l(t,p)\,\mathrm {d} t=\int _{0}^{1}{\tilde {\mathbf {T} }}:{\dot {\mathbf {E} }}\,\mathrm {d} t=\int _{0}^{1}{\dfrac {1}{2}}{\tilde {\mathbf {T} }}(t,p):{\dot {\mathbf {C} }}(t,p)\,\mathrm {d} t\\\approx &\displaystyle \sum _{i=0}^{999}{\dfrac {1}{2000}}{\tilde {\mathbf {T} }}\left({\dfrac {i+\xi }{1000}},p\right):{\dot {\mathbf {C} }}\left({\dfrac {i+\xi }{1000}},p\right)\,.\end{aligned}}}$

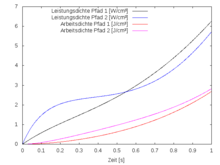
Deformation work and performance along the two paths are numerically evaluated using ${\displaystyle \xi ={\frac {1}{2}}}$

Because the power increases monotonically with time at n = −2, see figure on the right, one obtains a lower limit with ξ = 0 and an upper limit with ξ = 1 for the voltage work performed. With the material parameters G = 1 MPa and γ = 7 MPa one calculates:

${\displaystyle {\begin{aligned}2{,}6795\,\mathrm {MPa} \leq \psi (t,0)\leq 2{,}6857\,\mathrm {MPa} \\2{,}8214\,\mathrm {MPa} \leq \psi (t,1)\leq 2{,}8271\,\mathrm {MPa} \end{aligned}}}$

One MPa corresponds to one joule per cubic centimeter (J / cm³). With n = −2, different deformation work is done along the two paths, which is why the material is then not hyperelastic.

One could now load less than 2.7 J / cm³ along the first path and relieve the load along the second path, with more than 2.8 J / cm³ jumping out. So you would get more than 0.1 J / cm³ of energy per cycle. By running through the cycle several times, you could generate any amount of energy. But that contradicts thermodynamic principles. The hyperelasticity , which is a special case of Cauchy elasticity, avoids this contradiction.

See also

• Elasticity theory
• Hypo-elasticity
• Rheology
• Viscoelasticity
• Newtonian fluid
• Formula collection tensor algebra
• Tensoranalysis formula collection

Footnotes

1. ↑ Bestehorn (2006), p. 52.
2. ↑ Haupt (2000), pp. 279ff
3. ↑ Bestehorn [2006], p. 57.
4. ↑ This derivation is also named after C. Truesdell. He himself named the derivative after Cauchy and wrote in 1963 that this rate was named after him for no inventive reason ("came to be named, for no good reason, after [...] me") see C. Truesdell: Remarks on Hypo-Elasticity , Journal of Research of the National Bureau of Standards - B. Mathematics and Mathematical Physics, Vol. 67B, No. 3, July-September 1963, p. 141.
5. ↑ ^{a b} The Fréchet derivative of a scalar function according to a tensor is the tensor which - if it exists - corresponds in all directions to the Gâteaux differential , i.e. ${\displaystyle f}$ ${\displaystyle \mathbf {T} }$ ${\displaystyle \mathbf {A} }$ ${\displaystyle \mathbf {H} }$

   ${\displaystyle \mathbf {A} :\mathbf {H} =\left.{\frac {\mathrm {d} }{\mathrm {d} s}}f(\mathbf {T} +s\mathbf {H} )\right|_{s=0}=\lim _{s\rightarrow 0}{\frac {f(\mathbf {T} +s\mathbf {H} )-f(\mathbf {T} )}{s}}\quad {\text{für alle}}\quad \mathbf {H} \in {\mathcal {L}}}$

   applies. The scalar is a real number . Then will too ${\displaystyle s}$

   ${\displaystyle {\frac {\partial f}{\partial \mathbf {T} }}=\mathbf {A} }$

   written.
6. ↑ JC Simo, KS Pister: Remarks on Rate Constitutive Equations for Finite Deformation Problems: Computational Implications . In: Computer Methods in Applied Mechanics and Engineering. 46, 1984, pp. 201-215.
   The associated strain energy density is

   ${\displaystyle {\begin{aligned}\psi =&{\dfrac {G}{4\rho _{0}}}\operatorname {Sp} (\mathbf {C\cdot C} )-{\dfrac {G}{2\rho _{0}}}\operatorname {Sp} (\mathbf {C} )+{\dfrac {\gamma }{4\rho _{0}}}\ln(\operatorname {det} (\mathbf {C} ))^{2}\\\rightarrow {\tilde {\mathbf {T} }}=&\rho _{0}{\dfrac {\mathrm {d} \psi }{\mathrm {d} \mathbf {E} }}=2\rho _{0}{\dfrac {\mathrm {d} \psi }{\mathrm {d} \mathbf {C} }}=G(\mathbf {C} -\mathbf {1} )+\gamma \ln(\operatorname {det} (\mathbf {C} ))\mathbf {C} ^{-1}\end{aligned}}}$

literature

• H. Altenbach: Continuum Mechanics . Springer, 2012, ISBN 978-3-642-24118-5 .
• M. Bestehorn: hydrodynamics and structure formation . Springer, 2006, ISBN 978-3-540-33796-6 .
• P. Haupt: Continuum Mechanics and Theory of Materials . Springer, 2000, ISBN 3-540-66114-X .