Shear (mechanics)
In mechanics, shear results from the effect of an offset pair of forces , the shear force or shear force , on a body and leads to a shear distortion of the area between the forces. This means that a previously rectangular area would deform into a parallelogram , see also: Shear (geometry) .
The couple of forces can also be brought about by a moment acting on the body . A couple of forces, which lies on a line, causes instead of the shear strain is a strain of the body.
At the same time as the shear distortion , the force couple creates a shear stress in the material, which is also referred to as shear stress . The shear modulus describes the size of the distortion relative to the applied shear stress.
In continuum mechanics , shear and shear strain are used synonymously, see section Kinematics of Shear .
In technical mechanics , shear is also understood to mean shear stress , see section Dynamics of Shear .
Of pure shear is used when considered in the section plane not normal strains or no normal stresses occur.
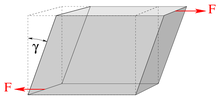
Shear occurs, among other things, in torsion as in the picture or the transverse force loading of beams , but is also significant in viscous fluids ( liquids or gases ).
introduction
The shear of liquids and gases is covered in a separate section below.
Macroscopic observation
Two forces acting parallel to each other in opposite directions acting on a body cause the body to shear and are therefore called shear forces , see picture. In the case of torsion, surfaces lying parallel to each other are twisted against each other, which also represents a shear, see introductory picture above. The length of the object and its cross-section ideally remain unchanged. The shearing forces always act tangentially to the body surface. Typical examples of shear forces occur in rivet and bolt connections, see Shear (statics) . The cutting edges of scissors separate the material to be cut by shearing ( shear cutting ).
Microscopic observation
The strength of materials and continuum mechanics interested in the local conditions in a body under shear, because there is decided whether or not the body, for example, elastically or plastically deformed. The local conditions become accessible when the body is mentally cut up and thus cutting stresses ( vectors with the dimension force per area ) arise at the cutting plane , which depend on the orientation of the cutting plane. The cutting plane can be placed at a point so that the shear stress, which by definition acts parallel to the cutting plane, is at its maximum. In contrast, normal stresses act perpendicular to the cutting plane.
The loads used in the macroscopic analysis lead to shear stresses that are at a maximum compared to the main normal stresses (principal stresses for short), namely the same amount. Here two principal stresses are oppositely equal (see also the example below) and the center of Mohr's stress circle lies in the stress space at the origin, so that the maximum shear stress is just as large as the principal stresses. The Mohr stress circle also shows that the maximum shear stresses occur at a 45 ° angle to the main stress directions, which in turn are perpendicular to cutting planes in which no shear stresses occur, see figure.
If two principal stresses are the same, the Mohr stress circle degenerates to a point. If all three main stresses are the same, then the material point is under all-round pressure / tension and there are no shear stresses in any plane. In all other cases there are sectional planes in which a maximum and non-zero shear stress occurs.
The cases presented in the macroscopic analysis represent the most unfavorable loads from the point of view of the shear stress hypothesis, because according to this hypothesis, the shear stresses are responsible for the failure of a material. It is therefore worth paying special attention to the thrust components and aligning the reference system accordingly.
Shear kinematics
To illustrate a shear, you can imagine a book : if you move the book covers parallel to each other, the spine and page stacks form an angle other than 90 °. The deviation from the right angle is the shear distortion or slip γ.
Mathematically, a local deformation is considered as in the picture on the right. Two material lines crossing each other in the reference state (upper part of the picture) (which can be imagined as lines scratched on the surface) enclose a right angle , which is measured between their tangent vectors and . As usual, the x and y coordinates are numbered according to the scheme x → 1 and y → 2. In the course of a deformation - described with the motion function - the angle γ between the tangent vectors changes according to
- With
The tensor E is the unit-free Green-Lagrange distortion tensor , the components of which relate to the base system formed by the vectors in the reference state , and “ ” is the Frobenius scalar product of vectors. The component is the shear strain in the 1-2 plane and and are normal strains that occur in the 1 and 2 directions.
In the case of small distortions , the Green-Lagrange distortion tensor changes over to the linearized distortion tensor , and the denominator in the above fraction can be set equal to one with the result
The components refer to a Cartesian coordinate system which is aligned parallel to the vectors , in which X 1,2 are the coordinates, u 1,2 are the displacements and ε 12 the shear distortion.
The shear rate is calculated in the state γ = 0 ° with the Verzerrungsgeschwindigkeitstensor d from
Here the mutually orthogonal tangent vectors are selected in the deformed state. The components relate to a Cartesian coordinate system, which is now aligned parallel to the vectors , in which x 1,2 are the coordinates, v 1,2 are the speeds and d 12 is the shear distortion speed . With small distortions and the shear rate is:
Shear in geology
In geology, a distinction is made between the two end links pure shear (also coaxial shear or pure compression ) and simple shear (also non-coaxial shear ). A simple shear includes an additional rotational component compared to pure shear. These two components are also used in the discussion of transpressive (compression plus lateral movement) and transpressive (extension plus lateral movement) tectonics .
Shear dynamics of solids
A shear load is a force or a moment at which the loaded body executes a shear movement at least locally. This external load is converted into tensions in the body, in particular shear stresses. Shear stress does not only occur with external stress, but also, for example
- in the case of thermal stress on bodies that are connected to one another and have different coefficients of thermal expansion ,
- due to latent stresses with inhomogeneous solidification, for example during welding, or
- For coatings that shrink differently after application than the base material.
In the case of shear - or generally in the case of a shear load - the relationship between the shear stress τ and the shear distortion or sliding γ is in the geometrically linear range and in the case of linear elasticity
The proportionality constant G is the shear modulus (also: shear or slip modulus). The shear stress is also called shear stress and has - like the shear modulus - the dimension of force per area. The SI unit is therefore the Pascal (Pa), i.e. N / m² - Newton per square meter .
When sheared in the elastic area in the body, material surfaces are shifted locally , reversibly, parallel to one another. The surface can warp, as happens, for example, with the torsion of a non-circular rod or the transverse force loading of a beam. If the shear strength is exceeded , the workpiece is sheared off (see the examples on torsional fracture ). Outside the elastic range until the shear strength is reached, ductile materials deform plastically , which is discussed below.
Shear of crystalline materials
If the shear load exceeds the elasticity limit , dislocation movements occur in ductile crystalline materials - especially metals . In a crystalline material, crystal parts are shifted against each other during shear. The plane that separates the crystal parts from each other is the sliding plane , which together with the sliding direction forms the sliding system . In the example with the book, the slip planes would be the book pages, which now slide on each other in the slip direction perpendicular to the book spine in the paper plane. If the normal vector of the slip plane and the slip direction in the plane, then the shear stress in the slip system (GS) is given by the stress tensor :
If the critical shear stress is exceeded by the shear stress in the slip system, the atoms slide off each other on both sides of the slip plane and plastic deformation occurs.
Shear of polycrystalline materials
In polycrystalline, isotropic materials, the crystal orientation changes with the crystal grains, the deformations of which can hinder each other, which increases the shear yield point. The relationship between the shear yield point and the critical shear stress is the Taylor factor M:
For a face-centered cubic lattice , M = 3.1 and for a body-centered cubic lattice , M = 2.9. The Taylor factor is calculated from the statistical properties of the crystal grains in the polycrystal.
Shear of thermoplastics
Thermoplastics can be plastically deformed by locally stretching the chain molecules that make them up. This creates - especially under pressure - shear bands that are oriented at an angle of 45 ° to 60 ° to the direction of loading, where localized large plastic deformations of 100% and more occur, apart from which the deformations are small.
Shear of fluids

Shear is also significant in fluids and the shear rates in them are calculated as described in the section on kinematics. In frictionless liquids and gases , however, the shear rates do not lead to shear stresses. The fluids mostly considered in fluid mechanics are Newtonian fluids , whose velocity field obeys the Navier-Stokes equations . The material model for Newton's fluid is:
Here, p is the pressure, which is generally dependent on the density ρ, λ and μ are the first and second Lamé constants , Sp is the trace and 1 is the unit tensor . The shear stresses are therefore proportional to the above-mentioned strain rate tensor, which is macroscopically noticeable as viscosity .
On walls where the sticking condition does not allow the fluid to move parallel to the wall, the shear stress leads to the formation of a boundary layer in which the speed is equal to the speed in the main flow, see picture. If the fluid flows in the x-direction parallel to the wall and the wall normal points in the y-direction, then the shear stress at a distance from a flat wall is:
because the term with the velocity perpendicular to the wall can be neglected here. In particular, the wall shear stress is defined by
Non-Newtonian fluids show a non-linear dependence of the shear stresses on the shear rates.
example
In the xy plane, the points of a unit square experience the shift
The parameter γ is the slip and φ causes a rotation. The linearized strain tensor is calculated from derivatives according to the location
which - unlike the picture - is only allowed in with the Hooke's law gives the stress tensor
as a function of the shear modulus G and the first Lamé constant λ. The operator Sp forms the sum of the diagonal elements ( trace ) and is the unit tensor . The shear stresses have the magnitude of the strain and stress tensor here - within the framework of the geometrically linear consideration - no normal components.
In cutting planes with normal vectors
no shear stresses occur because the intersection stress vectors point exactly in the normal direction ( are principal stresses and are the associated principal stress directions.)
The linearized strain tensor is the symmetrical part of the displacement gradient
By adding the non-linear component
the linearized strain tensor results in the Green-Lagrange strain tensor
When a square is sheared to form a parallelogram of the same area, normal strains occur with large shear movement, see Poynting effect .
Remarks
- ↑ The variable is case-sensitive. Variables in capital letters relate to the reference state and those in lower case letters to the current state, which can be greatly deformed and twisted compared to the reference state.
See also
Solid:
Fluids:
literature
- H. Balke: Introduction to Technical Mechanics. Strength theory . 3. Edition. Springer-Vieweg, 2008, ISBN 978-3-642-40980-6 .
- H. Altenbach: Continuum Mechanics: Introduction to the material-independent and material-dependent equations . Springer, 2012, ISBN 3-642-24119-0 .
Individual evidence
- ↑ a b Bernhard Grotz: Mechanics of solid bodies. October 30, 2015, accessed November 3, 2015 .
- ↑ Overview of meanings: shear (mechanics). Duden online, accessed on November 2, 2015 .
- ↑ J. Rösler, H. Harders, M. Bäker: Mechanical behavior of materials . 4th edition. Springer-Vieweg, 2012, ISBN 978-3-8348-1818-8 .





































![(x, y) \ in [0.1] \ times [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6d95b074f61bc9fac67a16e74107ccf025eee4e)











