Shear (geometry)
A shear or transvection is originally understood in the geometry of the plane to be certain affine images of the plane on itself, in which the surface area is retained. In the case of a shear, a straight line in the plane (the fixed point line or axis of the shear) remains fixed, that is, every point of this straight line is mapped onto itself. All other points of the plane are shifted parallel to the axis, the length of the displacement vector of a point is proportional to the distance of this point from the axis. All straight lines that are parallel to the axis are mapped onto themselves, i.e. fixed straight lines . Lines on these straight lines are shown true to length.
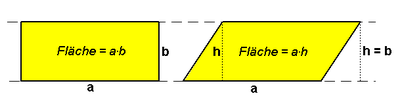
In the event of a shear, the distance between each point and the axis remains unchanged. This means that rectangles and triangles with one side parallel to the axis are mapped onto parallelograms or triangles that have the same height (perpendicular to the side that is parallel to the axis) (see the illustration).
The concept of (plane) shear can be generalized differently to affinities in space and in higher dimensions. Two ways in which the generalized shear does not change the volume of the figures depicted are presented here.
The successive application of a shear and a central extension (in either order) results in a shear elongation , not generally remain in the area and space content equal.
Shearings in the plane
An affinity of a two-dimensional affine space (the "plane") is a shear if and only if
- there are two different fixed points and are, formally:
- and any point that does not lie on the straight line connecting the two fixed points from (1), is below the fixed point or is moved parallel to . formally:
- .
From the first condition it follows with the properties of an affinity that the straight line connecting the two fixed points is a fixed point line (axis ). The second condition allows (with the possibility of a third fixed point outside of ) the identical mapping as shear or forces that with a point outside of the fixed point line all points outside of parallel to are shifted.
In general, an affinity in the plane is uniquely determined if the image points not lying on a straight line are specified for three points that do not lie on a straight line.
properties
It is noteworthy that no distance or area concepts have to be used to characterize a shear. Shearings can be defined in every affine plane. The properties mentioned in the introduction are then to be specified more precisely:
If a Euclidean distance and an area compatible with this distance are defined in the plane , then with a shear they remain with an axis
- the distance between two points that lie on or parallels ,
- the distance between two parallel lines and
- the ( oriented ) area of each measurable area
receive.
In the real plane, by choosing a "unit ellipse" or, equally, by choosing an affine coordinate system as the orthonormal basis, different Euclidean structures, i.e. H. Introduce different angles and spaces. A shear now has the mentioned invariance properties with respect to each of these structures, while for example a rotation with respect to one Euclidean structure need not be a rotation with respect to another. This independence from the Euclidean structure is shared by the shearings with the parallel displacements .
Image construction
An in-plane shear is defined when its axis and, for a given point off-axis, its image point are given. Then the image of a further point , which is not on the axis and not on the connecting line , can be constructed as follows, the figure on the right shows the steps (red) of the construction:
- Construct a parallel to through .
- Draw the straight line connecting it . It intersects the axis at a fixed point .
- Draw the straight line connecting it . It is the image of the straight line . Therefore the intersection of with is the desired pixel.
If the point to be mapped lies on the axis, it is itself a fixed point. If it lies on the connecting line , then either according to the construction text above, the image point must first be determined for an auxiliary point outside of and the axis, or the fact that the shear acts on as a displacement is used for the image construction .
Matrix display
If you choose a Cartesian coordinate system in the plane , in which the axis coincides with the axis of the shear, then this shear is represented by the linear mapping
with the mapping matrix
shown. If, on the other hand, the axis of shear is the axis, and swap their places in the mapping matrix. Both images change the angle between the coordinate axes .
If an affine mapping of the plane is given by its mapping matrix and its displacement ,
- ,
then there is a shear if and only if
- the fixed point equation a solution has
- and the matrix has the characteristic polynomial . The determinant is given as
- .
For algebraic investigations, it is convenient to represent the affine mappings under consideration as 3 × 3 matrices (extended mapping matrices) with respect to a fixed basis. This corresponds to a representation of the affine mapping in homogeneous coordinates : Instead of
then you write
- .
Algebraic structure
The concatenation of two shears is generally no longer a shear. In particular, the set of all shearings of the plane does not form a group . Your extended mapping matrices are a subset of the group of displacement matrices in the special linear group . That's a group. (It consists of the matrices of the form
- ,
whose determinant is 1. Exactly the extended mapping matrices of area-true and orientation- preserving affinities form this group.)
The set of shears with a common axis forms an Abelian group . It is isomorphic to the group of displacements in a fixed direction, because one can choose an affine or Cartesian coordinate system (with the common axis as the axis) in which they all represent the shape
to have. The position of the origin on the axis is not important for the representation of the shear.
For shearings whose axes are parallel, one can choose a common affine or Cartesian coordinate system in which their extended mapping matrices form
to have. (The shift component must vanish, otherwise the fixed point equation has no solution.) If you multiply two of these extended matrices, the result is:
- .
From this it becomes obvious:
- The concatenation of two shears with parallel axes is again a shear with an axis that is parallel to the original axes.
- The set of shears with axes in a fixed direction forms an Abelian group.
- The group is created from the group of shears with a fixed axis (from the family of parallels) and the group of displacements parallel to this axis. In fact, it is the direct product of these groups.
- The group is isomorphic to the group of parallel displacements of the plane (i.e. ultimately to the two-dimensional vector space above the basic body as an Abelian group).
Shearings in higher-dimensional spaces
In a -dimensional space, a shear is an affinity that has a fixed point hyperplane and by means of which all points not lying on this hyperplane are shifted in a fixed direction parallel to the fixed point hyperplane. The length of a displacement vector is again proportional to the distance from the fixed point hyperplane.

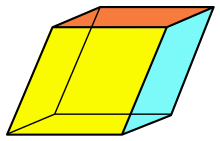
The figure on the right shows how the image of a cuboid is deformed into an oblique prism in such an image , if the base side (red) lies in the fixed point plane and the shear acts parallel to the front side (yellow). In the picture, the red and light blue sides and the opposite sides remain rectangles .
The generalization to higher-dimensional spaces is not uniform in the literature. Any affinity that is a matrix representation of form is also more generally referred to as shear of -dimensional space
(if a suitable basis is chosen). There are standard matrices and is any matrix. With such a shear, the fixed space is a linear space of dimension (see rank (mathematics) ).
The figure on the right shows the effect of the more general form of a shear on a cuboid in three-dimensional space. The shown parallelepiped emerged from such a shear from a cuboid. The (oriented) volume of the parallel piped corresponds to that of the original cuboid.
Both transfers of the term shear in planar geometry to higher dimensions describe content-true affinities that leave an at least one-dimensional affine subspace fixed point by point. Every shear of a -dimensional space in the general sense (with a fixed point straight line) can be represented as a sequential execution of (at most) shearings in the more special sense (with one fixed point hyperplane each). All fixed point hyperplanes of the more specific shearings contain the fixed point line of the more general ones. If there is a scalar product in the -dimensional space and if the generalized shear has the above-mentioned matrix representation with respect to an orthonormal basis of the space, then the fixed point hyperplanes can be chosen orthogonal to each other for the special shearings from which the general one is composed.
Shear elongation
A shear extension occurs when a centric extension and a shear are performed one after the other (in any order). In the plane it can be brought to the normal form by choosing suitable coordinates (see the main article Jordan normal form ). It has no axis (fixed point line), but a clear center (fixed point). If a shift is also carried out, a shear extension occurs again, whereby the center can change.
Relation to the term shear in mechanics
In mechanics , especially in continuum mechanics , the term shear is used to describe certain deformations of a three-dimensional body. Mass elements of the body are shifted in a common direction parallel to a fixed plane in the body and the length of the displacement vector is proportional to the distance of the mass element from the fixed (fixed point) plane. The term thus coincides (as an illustration) with the more specific generalization to three dimensions, which is described above. If you choose the coordinate system so that the unshifted plane forms the xy plane of the Cartesian coordinate system and all shifts take place parallel to the x-axis , then the three-dimensional shear can be achieved through the linear mapping
describe. It is the displacement of the mass element at a distance from the fixing point plane. This is explained in the main article Shear (Mechanics) .
literature
- H. Schupp: Elementary Geometry . UTB Schöningh, 1977, ISBN 3-506-99189-2 , p. 150 .
- Hermann Schaal: Linear Algebra and Analytical Geometry . 2nd Edition. Vieweg, Braunschweig 1980 (3 volumes: ISBN 3129228217 , ISBN 3528130571 , ISBN 3-528-13058-X ).