Strength theory
| The strength theory in technical mechanics | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The strength of materials is a branch of engineering mechanics . Their main areas of application are construction ( structural engineering ) and mechanical engineering . Their laws are used to investigate whether structures or machines can withstand the loads imposed on them , ie not break or deform excessively . Due to the inclusion of deformation, the expanded term strength and deformation theory is often used.
With their help, the stress in the body resulting in voltages compared and the deformations occurring on the body with the permissible values. The permissible stresses are essentially determined by the material used and the permissible deformations by the use of the components.
In the case of elastic deformations, the term elastostatics is used in addition to strength theory . Plastic deformations are the subject of plasticity theory .
history
In ancient times and in the Middle Ages, the builders used tradition, experience and intuition to determine the strength of buildings and machines so that they neither failed nor were overdimensioned. The first concrete experiments on how different materials behave when exposed to loads were carried out by Galileo Galilei at the beginning of the 17th century. Systematic and reliable results were achieved from around 1800 in particular by Claude Louis Marie Henri Navier , Adhémar Jean Claude Barré de Saint-Venant , Gabriel Lamé , Siméon Denis Poisson and Christian Otto Mohr . The names of these scientists can still be found today in terms of strength theory named after them. The field of strength theory includes large parts of elasticity and plasticity theory , as well as the creep (viscosity) of solids. The strength theory is used today in particular for calculations in construction and mechanical engineering .
Basics
tension
Mechanical tension (short: tension) and distortion are the two fundamental quantities of strength theory. Strength of strength is mainly concerned with the micro and macro level , where in continuum mechanics , strictly speaking, only stresses are present. These stresses are combined into the resulting forces and moments at the cross-sectional level and interact with the structural analysis . Strength of materials also deals with the stresses in the cross-section that cause the stress results - these are equated with the internal forces in the first order theory in structural engineering. The following results are of particular interest for structural analysis: normal force , shear force , bending moments and torsion moment . The distribution of these loads inside the body is represented by the tension. The elementary concept of tension, tension equals force per area, was coined by Augustin-Louis Cauchy in 1822.
The normal stress is introduced by normal forces or force components orthogonal to the observed surface . It follows that the mean stress in the longitudinal direction is the normal force per cross-sectional area.
The bending moment also depends on the tension in the longitudinal direction from: .
Shear forces are absorbed by cross sections through shear stress. In the case of rectangular cross-sections with a height h (in the z-direction) and the x-axis in the center of gravity, which are stressed in the main axes of inertia , it should be noted that the shear stresses in the theory of elasticity have a quadratic course over the cross-section, since on the free surface ( in general) for the shear stresses applies and due to the symmetry of the stress tensor implies that the shear stresses for zero.
The above equations are not sufficient to clearly dimension a cross-section, there are an infinite number of cross-sectional parameter combinations (e.g. ). Furthermore, even voltage component interactions at material level (eg. Comparison voltage to be considered); and in general (both in the theory of elasticity and in the theory of plasticity ) it must be demonstrated for each fiber of the material that certain strength criteria are observed.
Strictly speaking, the stress is a tensorial quantity, it is called a stress tensor to illustrate this :
There are three normal stresses on the main diagonal . The trace of the stress tensor is invariant of the coordinate system. The remaining elements represent the shear stresses. Due to the symmetry of the stress tensor, there are three independent shear stresses. By transforming the principal axis , each stress state can be converted into a coordinate system in which all shear stresses disappear (eigenvalue / eigenvector problem).
The Mohr stress circle is a graphical method for determining principal stresses, their directions and principal shear stresses .
distortion

In the mechanics of deformable bodies, every tension on a body is accompanied by a distortion - and thus a deformation - of this body. The elementary concept of distortion is commonly referred to as distortion, i.e. H. understood as the quotient of the change in length to the original length:
Like tension, distortion is a tensile quantity:
Since in the technical application the considered displacement derivatives (i.e. distortions and rigid body rotations) are generally small compared to 1 ( ), it is common to use the linearized strain tensor instead of the Green-Lagrange strain tensor .
The main diagonal elements of the linear strain tensor describe the strain , defined as the relative change in length of a line element . The remaining elements of the strain tensor describe the shear , defined as the symmetrical half of the angle change between two originally orthogonal line elements at the point of intersection. The change in angle corresponds to twice the shear strain components in the strain tensor.
Stress-strain diagram
The stress-strain diagram often results from measurement data (e.g. a tensile test ) and establishes a relationship between stress and distortion by plotting the strain on the abscissa and the stress (usually the normal stress) on the ordinate . For ductile materials, the functional relationship can often be divided into a linear-elastic range, a non-linear-elastic range and a plastic range. For strength theory, the linear-elastic range is sufficient, depending on the material and application. However, in steel construction , concrete construction and timber construction , the elastic range (except in special cases) is left in a static calculation . In timber and concrete construction, the distortions are generally assumed to be linear over the cross-section ( Bernoulli's assumptions ), however, according to current standards, a plastic plateau (e.g. block distribution or parabolic-rectangular distribution) is assumed with regard to the stress distribution in concrete construction . In steel construction, there is a cross-sectional classification in the current standardization , which defines which processes are permissible, whereby the profiles standardized in construction are i. d. Usually meet the highest class (namely class 1). However, they are mostly only proven for class 2 (plasticizing the cross-section, but no rotation capability assumed) or only for class 3 (elastic) - lying on the safe side.
In the linear-elastic range, the graph describes a straight line; the generalized Hooke's law applies . Here is the elasticity tensor . The moduli of elasticity can be determined by ultrasonic testing . Modulus of elasticity are also determined by (uniaxial as well as multi-axis) compression or tensile tests in the linear-elastic range. The elasticity quantities are important quantities for the design of bodies in strength theory.
With reference to the stress-strain diagram, the yield stress is usually defined. Failure criteria for (single or multi-axis) strengths are often defined from the stress-strain diagram. These strengths are used when choosing the material for a given application. Thus, in the construction industry frequently reinforced concrete used, in which case in the static calculation i. d. Usually only tensile stresses are assigned to steel and only compressive stresses to concrete.
Shear stress-shear diagram
The shear-shear diagram often results from the measurement data of the stress of a sample to shear . In the shear stress-shear diagram, the shear is plotted on the abscissa and the shear stress on the ordinate. In the linear-elastic range, the graph of the shear stress-shear diagram is linear. In the strength of materials, elastic in the linear range applies: . The constant of proportionality is the shear modulus .
Thermally based stresses
When the temperature rises, a material usually expands ( thermal expansion ); when the temperature falls, it contracts. This relationship can be linearized and modeled using the following equations:
and
- .
Here is
- the change in temperature
- the coefficient of thermal expansion
- the change in length of a body
- its original length.
If the expansion is prevented:
- ,
it follows that the distortion due to the stress ( constraint ) is equal to the negative temperature expansion:
- .
Area moment of inertia

The properties of the material and the geometry of a body influence its behavior under load. The geometrical moment of inertia is a purely geometric measure of the resistance of a cross-section through a body to deformation due to bending and torsion . A distinction is made between the polar area moment of inertia , the axial area moments of inertia and the moments of deviation .
The moment of inertia can be beyond tensorial conceive; it applies . The area inertia tensor is denoted by, because it is already used for the identity .
The eigenvalues of the area inertia tensor are the maxima of the axial area moment of inertia in a center of gravity system and are called the main moments of inertia. Transformation relationships can be used to determine the main moments of inertia .
In order to be able to calculate the geometrical moments of inertia of complex cross-sectional areas more easily, a breakdown into partial areas and the calculation of the geometrical moments of inertia of these partial areas can take place. If the center of gravity of a partial area does not coincide with the overall center of gravity, the Steiner share must be added to the axial area moments of inertia and the moments of deviation according to Steiner's theorem .
The geometrical moment of inertia is of great practical importance because with its knowledge, components can be designed to be as resistant as possible for a given main load direction and a given material use. This is the reason for the frequent use of profile steels , such as the double T-beam, instead of solid material.
Statements on cross-sectional loading
Following the considerations of statics (e.g. structural engineering ) or dynamics (e.g. structural dynamics ), the same loads are assigned to the same load, referring to a line passed through an elastic rod. The subject of strength theory is the strength of strength theory which stresses result from such loads in the cross-section.
Bend
Statements about stresses and deformations in bodies due to bending are an elementary component of strength theory. Here, in the is beam theory the model of the beam used, since a number of components, in particular structural components and waves leave, modeled as beams.
A general distinction is made between a straight bend and an oblique bend . The straight bend occurs by loading along the main axes of inertia of a beam; in the case of axially symmetrical cross-sections, these are the axes of symmetry.
Bending normal stress
When a beam is bent by a moment or a load that generates a bending moment, normal stress occurs in the beam. Since the beams examined are mostly long in relation to their thickness ( slender beam ) and the deflections are relatively small, it is often assumed that the normal bending stress changes linearly over the cross-section (see figure on the right). In the case of a straight bend, the normal bending stress only depends on one main axis of inertia. The magnitude of the largest bending normal stresses occurs on the fiber of the beam that has the largest or smallest value on this main axis of inertia. If there is no normal force , the zero crossing of the stress (the zero line or the neutral fiber ) goes through the center of gravity of the cross section. In this case, in the case of a straight bend, the sign of the stress only depends on the sign of the main axis of inertia, provided that the member's longitudinal axis is in the center of gravity.
With linear elasticity and assuming Bernoulli beam theory, the bending stress during bending can be determined as follows:
In the case of stress in the main axes of inertia, the stress components are bending stresses (a type of normal stresses ) depending on , and , the distance to the x-axis (rod longitudinal axis), the loading bending moment around the y-axis and the axial geometrical moment of inertia . If, in addition to the load caused by a bending moment, a beam is subject to a normal stress ( constraint ) caused by a change in temperature due to hindered (or prevented) elongation , the resulting normal stress can be determined in the linear elasticity theory according to the superposition principle by adding the normal stress caused by the bending moment to the thermally induced normal stress . For the dimensioning of real beams, the edge stresses are often decisive in the linear elasticity theory, since with only bending normal force torsion stresses the stress in the rest of the beam is always the same or less than the stress on the edges. In the case of M - N - V interaction, each fiber must be verified, especially in the center of gravity, since this is where the largest shear stresses are present. In order to have a material optimization (larger lever arm), cross-sections with (possibly continuously) graded material strengths or material widths can be produced, or material composites can be used as in reinforced concrete construction . If you insert the edges of the beam into the bending stress formula, the result is that with only uniaxial major axis bending in the z direction:
Since both as well as geometric quantities, which depends only on the x-coordinate, are, bending normal voltages, for a given cross-section, for a given load and linear elasticity can be determined unambiguously, and may include, for resisting torque be summarized.
It applies and thus .
The section modulus is also a purely geometric variable and is often used when dimensioning beams, since the maximum stresses given by the choice of material must not be exceeded and the section modulus creates a simple relationship between the normal bending stress and the stress caused by a bending moment.
strain
A bending bar (e.g. beam on two supports or a cantilever arm) is stressed with a positive strain in the usual coordinate system by a positive moment around the positive y-axis on the side with a positive z-coordinate. Only the zero line plane, in which there are no stresses, which runs through the center of gravity of the cross-section of the beam when only bending moment is applied, remains free of normal stress in Bernoulli beam theory and thus maintains its length (at constant temperature). Since Bernoulli's assumptions apply to a good approximation for long beams , every cross-sectional area along the beam remains flat and orthogonal to the beam axis.
The bending line describes the deflection of the bar axis of a beam at any x-coordinate. It generally consists of elastic, plastic and viscous components. In the linear elasticity theory, the bending line can be obtained via differential relationships through multiple integration from the bending moment curve, shear force curve or line load, provided that it can be clearly adapted to the boundary conditions. The following applies when the temperature is constant over the cross section and when the main axis is (uniaxial) bending:
- .
Here is the modulus of elasticity, the axial geometrical moment of inertia in the z-direction and the deflection component in the z-direction. The integration constants can exclusively with statically determined and statically indeterminate systems clearly about the storage are determined of the bar.
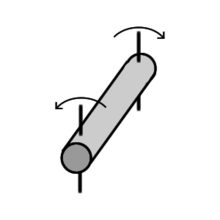
torsion
If a rod is stressed by a torsional moment, torsional shear stresses occur in its interior, which cause an infinitesimal displacement of its cross-sectional surface elements. In most cases, the component safety against torsional stress must be proven in a proof of stability .
Torsion of bars with a circular cross-section
In the case of torsion of circular rods such as drive shafts and tubes , the cross sections remain flat and circular and straight lines remain straight in the axial direction. The radius and length of the rod remain constant for the small angles of rotation that occur in technology. In the linear elasticity theory, the torsional shear stress increases linearly with the radius and is dependent on the torsional moment and the polar area moment of inertia . It is calculated using the torsion formula
- .
As a result, the torsional shear stress is greatest on the surface of the rod and constant over the entire surface.
The angle of rotation of bars with a circular cross-section is calculated using the following formula:
Here, the length of the rod and G the shear modulus .
For shafts that have several shoulders of different diameters, the total angle of rotation can be calculated by using the above formula for each shaft step and adding the results.
Torsion of bars with a prismatic cross-section
While in bodies with a circular cross-section the cross-sections always remain circular under torsional load, warping occurs in prismatic cross-sections , which leads to a complex twisting pattern that cannot be determined with simple analytical means . When designing prismatic rods for torsion, tables are often used.
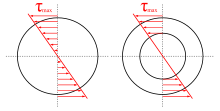
In the case of triangular or square cross-sections, the maximum shear stresses always occur at the midpoints of the side surfaces (see figure on the right), while the corners must be stress-free due to the stress boundary conditions.
Torsion of bars with thin-walled cross-sections
Since the maximum shear stress of circular cross-sections occurs at their edges, thin-walled cross-sections can be used, for example in pipes or hollow shafts .
The maximum shear stress on a thin-walled cross-section can be determined by using the torsional moment of inertia and the wall thickness .
If the torsional moment and wall thickness are combined to form the torsional resistance moment , the following applies .
The twist angle is calculated by .
In the case of thin-walled cross-sections, shear flow occurs, which is determined by the following relationship derived using Bredt's formula :
Here is the thrust flow and the area enclosed by the profile center line. The thrust flow is the reason for the significantly higher resistance of closed profiles compared to slotted profiles.
Buckling of compression rods
Very slim rods tend to fail suddenly due to lateral deflection as soon as one approaches a critical load - also known as Euler's buckling load in honor of Leonhard Euler . This effect is called "buckling" and has to be verified in the structural safety analysis. For the interpretation it is enough i. d. As a rule, it does not rule out that the critical load is simply kept below the computationally determinable ("theoretical") load capacity of a rod, since material or constructional imperfections can cause buckling before the ideal buckling pressure is reached. The critical load of a single bar that is only subjected to normal force is determined by:
Here is the modulus of elasticity , the area moment of inertia of the cross-section, the length of the rod and a length factor that depends on the boundary conditions (in special cases one of the Euler cases) (see picture on the right, from left to right). The buckling length is the (possibly virtual) distance between two turning points (moment zero points) of the (possibly extended) bending line of this single member. Effective length diagrams are often used for frames as well as rotatably mounted members (this almost always occurs to a good approximation in reality).
Deformation energy

Through its deformation takes physical energy, the strain energy on. For normal and shear stresses within a body, the deformation energy is determined by
Where:
- the stress tensor
- the distortion rate tensor
- the volume of the body under consideration
- the time.
For bars and beams, the deformation energy can be expressed as a function of the loads that occur. Here, the length of the body and the Laufkoordinate in the direction of the rod or beam axis.
The deformation energy is in the linear elasticity theory for loading by ...
- Normal force: with the normal force and the cross-sectional area .
- Bending moment: with the bending moment and the axial geometrical moment of inertia in the direction of the beam axis.
- Shear force shear: with the shear force and the form factor that contains the static moment and the width or wall thickness .
- Torsion: with torsion moment and polar area moment of inertia .
In the case of a combined load from several of these types of load, the resulting deformation energy can be determined by adding the individual deformation energies.
Energy methods

With the help of the deformation energy and different sets of energy methods, statements can be made about the behavior of a body under load.
- The set of Castigliano indicates that the partial derivative of the elastic linear body in a stored strain energy by the external force , the displacement of the force application point in the direction of this force results.
- The set of Menabrea indicates that the partial derivative of the strain energy for a static non-specific bearing reaction is zero.
- The Betti's theorem deals with a body, engage the two independent forces, and provides a connection between the working forth that perform these forces on the displacement force of each other.
- The principle of virtual forces is attributed to Johann I Bernoulli , is a modification of the principle of virtual work and enables the determination of displacements and angle changes in places where no force acts on the body. For this purpose, a virtual force is introduced at the desired location, which has any value other than zero.
Reliability in strength calculations

Inaccuracies occur in the case of machine components or elements of a building; these should be within the specified tolerances. On the one hand, manufacturing errors can reduce the load-bearing capacity that a component can take, and on the other hand, incorrect load assumptions can be made and the actual load on a part can exceed the assumed load. All commercial materials (especially wood or concrete ) have fluctuations in their strength that must be taken into account. The partial safety concept of the Eurocode describes one way of taking this into account, whereby the characteristic resistance and the characteristic action stand:
Whereby and not only tension or distortion, but also angle of rotation, temperature or the like can be. The failure load is generally determined by calculation models (standards, computer models ), which often contain data from tests or building damage.
The safety factor is dimensionless; its value is to be selected depending on the safety relevance of the component to be dimensioned and the scatter in the material behavior or the effect. In building construction, the global safety factor for concrete and timber construction is in the range of 2, in individual cases (nuclear power plants) it can (and must) be deviated from, extraordinary load cases (load cases that are not to be expected, e.g. car crashes) have a reduced safety factor on the action side (= 1) as well as on the resistance side (tw. = 1). Safety factors can often be found in standards .
In addition to the basic parameters such as stress and deformation, safeguards against long-term effects such as corrosion, creep and fatigue must be provided. Creep occurs when a material is subjected to uniform stress over a long period of time, often at high temperatures. Fatigue occurs with frequent load changes, for example in aircraft or in the drive shafts of vehicles.
literature
- Russel C. Hibbeler: Technical mechanics 2 strength theory. 8th edition. Pearson Germany, Munich 2013, ISBN 978-3-86894-126-5 .
- Walther Mann: Lectures on statics and strength theory. Revised and expanded edition. Teubner, Stuttgart 1997, ISBN 3-519-15238-X .
- Rolf Mahnken: Textbook of Technical Mechanics - Elastostatics, With an introduction to hybrid structures. Springer, Berlin 2015, ISBN 978-3-662-44797-0 .
- Klaus-Dieter Arndt, Holger Brüggemann, Joachim Ihme: Strength theory for industrial engineers. 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-658-05903-3 .
- Bruno Assmann, Peter Selke: Technical mechanics 2 - strength theory. 18th edition. Oldenbourg, Munich 2013, ISBN 978-3-486-70886-8 .
- Herbert Balke : Introduction to technical mechanics - strength theory. 3. Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-40980-6 .
- Dietmar Gross, Werner Hauger, Jörg Schröder , Wolfgang Wall: Technical Mechanics 2 - Elastostatics. 10th edition. Springer, Berlin / Heidelberg 2009, ISBN 978-3-642-00564-0 .
- Günther Holzmann, Heinz Meyer, Georg Schumpich: Technical mechanics - strength theory. 10th edition. Springer, Berlin / Heidelberg 2012, ISBN 978-3-8348-0970-4 .
- Volker Läpple: Introduction to strength theory. 3. Edition. Vieweg Teubner, Wiesbaden 2011, ISBN 978-3-8348-1605-4 .
- Herbert Mang , Günter Hofstetter: Strength theory. 4th edition. Springer, Berlin / Heidelberg 2013, ISBN 978-3-642-40751-2 (560 pages, springer.com ).
- Otto Wetzell, Wolfgang Krings: Technical mechanics for civil engineers. Volume 2: Strength of Materials. 3. Edition. Springer, Berlin / Heidelberg 2015, ISBN 978-3-658-11467-1 .
- Karl-Eugen Kurrer : History of Structural Analysis. In search of balance , Ernst and Son, Berlin 2016, pp. 380–439, ISBN 978-3-433-03134-6 .
Remarks
- ↑ Deformation (mechanics) #Strain measures in the English language Wikipedia
- ↑ x = X + u, where X is the reference configuration (usually undeformed) and x is the instantaneous system (usually deformed position)
- ↑ Deformation (mechanics) #Shear strain in the English language Wikipedia
- ↑ Multi-axis stress-strain diagrams often result from theories, assumptions, standards, ... and are not always confirmed by measurement technology or are e.g. B. purely fictional and are on the safe side.
- ↑ Many materials show viscous properties.
- ↑ Class 1: Plastic on cross-section, as well as system level plastic hinge ; Class 2: Plastic at the cross-sectional level, but not at the system level; Class 3: Elastic; Class 4: Due to local bumps, elastic calculation not allowed.
- ↑ Assumption does not apply in steel construction , for cross-section class 1 or 2.
- ↑ The stress components can also be negative and therefore smaller.
- ↑ This is the case when: My = Mz = T = 0.
- ↑ The steel is used on the tension side (for reasons of durability with sufficient concrete cover) in order to have an optimal lever arm for concrete compression.
- ↑ W_o is negative in the usual coordinate system.
- ↑ This also applies to a variable modulus of elasticity and a variable area moment of inertia.
- ↑ In concrete construction, you only need to prove the equilibrium torsion, but not the compatibility torsion.
- ↑ If the geometrical moment of inertia changes, you can usually assume the smallest geometrical moment of inertia in a limit load analysis , on the safe side.
Individual evidence
- ↑ a b c d e f g h i j k Russel C. Hibbeler: Technical Mechanics 2 Strength of Materials . 8th edition. Pearson Germany, Munich 2013, ISBN 978-3-86894-126-5 .
- ↑ a b c d e f g h i j k l Bernd Markert : Mechanics 2 Elastostatics - Statics of deformable bodies. 2nd Edition. Institute for General Mechanics Aachen , Aachen 2015.
- ↑ Herbert Mang , Günter Hofstetter: Strength theory . 4th edition. Springer, Berlin / Heidelberg 2013, ISBN 978-3-642-40751-2 .
- ↑ Major exercise on stability, elastic buckling, Euler cases. ( Memento of the original from March 4, 2016 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF) University of Magdeburg , accessed on October 10, 2015.