Area moment of inertia

This article covers resistance to bending or torsion. For the resistance to rotational acceleration see mass moment of inertia (moment of inertia).

Physical size
Surname	Area moment of inertia
Formula symbol	${\displaystyle I}$, out of date ${\displaystyle J}$
Size and unit system unit dimension SI cm 4 , mm 4 , m 4 L 4

The area moment of inertia , also known as area moment of the  2nd degree , is a geometrical variable used in strength engineering and derived from the cross-section of a beam , which was introduced to calculate deformation and stress in the event of bending and torsional stress . The formulas used contain the area moment of inertia in addition to other variables, such as those for the load and for the properties of the material used .

With the help of the geometrical moment of inertia, those loads are calculated which, if exceeded, lead to buckling of bars or buckling of shells .

The geometrical moment of inertia must not be confused with the (mass) moment of inertia , which characterizes the inertia of a rotating body with respect to angular acceleration .

species

symmetrical and asymmetrical cross-sections of a beam that is, for example, clamped on one side (1 and 2, cantilever beam ) subject to bending (3) or torsion (4).

Axial area moment of inertia

With the axial geometrical moment of inertia I _a , the cross-sectional dependency of the bending of a beam under load is summarized. The bending and the internal stresses occurring in the cross-section are smaller, the greater the axial geometrical moment of inertia. The most important dimension in the cross section is the expansion in the direction of the acting force. The picture on the right shows that a vertical load bends a beam less if it is arranged upright instead of flat (comparison between parts 1 and 2).

Polar area moment of inertia

The polar area moment of inertia I _p describes the area moment of inertia of a surface around a point to be defined (usually its center of gravity). The most important dimension in the cross-section is the radial expansion (R in part 4 of the adjacent figure). Only in the case of circular surfaces does the polar area moment of inertia correspond to the torsional moment of inertia . For other surface geometries, the torsional moment of inertia can usually only be calculated numerically. ${\displaystyle I_{\mathrm {P} }=I_{\mathrm {T} }={\frac {r^{4}\cdot \pi }{2}}}$

Biaxial moment of area

The biaxial area moment of inertia, also known as area deviation moment or area centrifugal moment, is used to calculate the deformation and the stresses

• with loaded asymmetrical profiles (part 3 in the adjacent figure)
• with asymmetrical loading, symmetrical (or any) profiles.

The area deviation moment or area centrifugal moment (unit m ⁴ ) must not be confused with the (mass) deviation moment or (mass) centrifugal moment (unit kg · m ² ).

calculation

units

The geometrical moments of inertia are usually given in cm ⁴ , mm ⁴ or m ⁴ (SI units). In the outdated system of units, which are still in use in the USA, they are usually notated in ⁴ .

Axial area moment of inertia

The axial geometrical moments of inertia can be described by these equations:

${\displaystyle I_{y}=\int _{A}z^{2}\ \mathrm {d} A}$

• z = perpendicular distance of the y- axis to the element d A

${\displaystyle I_{z}=\int _{A}y^{2}\ \mathrm {d} A}$

• y = vertical distance of the z -axis to the element d A

Both quantities can only have positive values.

Polar area moment of inertia

The polar area moment of inertia is composed of the two area moments of inertia and : ${\displaystyle I_{y}}$ ${\displaystyle I_{z}}$

${\displaystyle I_{\mathrm {P} }={\int _{A}r^{2}\ \mathrm {d} A}=I_{y}+I_{z}}$

Biaxial moment of area

The biaxial area moment of inertia is described by this equation:

${\displaystyle I_{zy}=I_{yz}=-\int _{A}zy\ \mathrm {d} A}$

This variable, also known as the deviation or centrifugal moment, is equal to zero if the y-axis or the z-axis is an axis of symmetry of the cross-section. The associated area moments of inertia are then called the main moments of inertia, in this case they take on extreme values. In contrast to the axial and the polar area moment of inertia, this quantity can have both positive and negative values. In addition to this definition with a negative sign , a definition with a positive sign is also used, depending on the literature; this must be taken into account in all formulas that use the moment of deviation.

Steiner's theorem

All geometrical moments of inertia mentioned here are related to a special point, namely the center of the area (center of area). For all other points, the geometrical moments of inertia can be calculated using Steiner's theorem .

Steiner's theorem states that the area moment of inertia of any cross-sectional area is composed of the area moments of inertia in the center points of the individual partial areas and the product of the square of the distance z from the total axis of the major axis to the partial area of ​​the major axis and partial area A. An application example is the I- Shape. The geometrical moments of inertia of the three rectangular partial areas, namely the two horizontal flanges and the vertical web, can be determined using the formulas given below and simply summed up for the vertical z-axis , because all the centers of gravity of the partial areas lie on the common center of gravity z of the total area. The geometrical moment of inertia with respect to the y-axis is also composed of the three summands plus the Steiner's part of the two flanges. ${\displaystyle I_{zz}^{*}}$ ${\displaystyle I_{yy}^{*}}$

${\displaystyle I_{yy}^{*}=I_{yy}+z_{s}^{2}\cdot A}$

${\displaystyle I_{zz}^{*}=I_{zz}+y_{s}^{2}\cdot A}$

${\displaystyle I_{yz}^{*}=I_{zy}^{*}=I_{yz}-y_{s}z_{s}\cdot A}$

The formulas are only valid if the geometrical moments of inertia are on the right-hand side of the equation, which refer to a coordinate system in the center of the area, while the geometrical moments of inertia on the left-hand side apply to any (parallel) coordinate system.

Area moment of inertia for any polygons

Moments of inertia of any closed polygons can be calculated using the following formulas if the points are entered counterclockwise. The moments of inertia refer to the origin of coordinates. The sign of the deviation moment conforms to the formulas for coordinate transformation. The polygon has n-1 points and starts with point 1 and ends with point n, which is identical to point 1. So the point i has the coordinates . ${\displaystyle I_{yz}}$ ${\displaystyle (y_{i},z_{i})}$

${\displaystyle I_{yy}={\frac {1}{12}}\sum _{i=1}^{n-1}(z_{i}^{2}+z_{i}z_{i+1}+z_{i+1}^{2})\cdot a_{i}\,}$

${\displaystyle I_{zz}={\frac {1}{12}}\sum _{i=1}^{n-1}(y_{i}^{2}+y_{i}y_{i+1}+y_{i+1}^{2})\cdot a_{i}\,}$

${\displaystyle I_{yz}=-{\frac {1}{24}}\sum _{i=1}^{n-1}(y_{i}z_{i+1}+2y_{i}z_{i}+2y_{i+1}z_{i+1}+y_{i+1}z_{i})\cdot a_{i}\,}$

${\displaystyle a_{i}=y_{i}z_{i+1}-y_{i+1}z_{i}\,}$

The formulas were derived using the Gaussian trapezoidal formula .

Principal Moments of Inertia and Twisted Moments of Inertia

${\displaystyle I_{\eta \eta }={\frac {1}{2}}(I_{yy}+I_{zz})+{\frac {1}{2}}(I_{yy}-I_{zz})\cdot \cos(2\cdot \phi )+I_{yz}\sin(2\cdot \phi )}$,

${\displaystyle I_{\xi \xi }={\frac {1}{2}}(I_{yy}+I_{zz})-{\frac {1}{2}}(I_{yy}-I_{zz})\cdot \cos(2\cdot \phi )-I_{yz}\sin(2\cdot \phi )}$,

${\displaystyle I_{\eta \xi }=-{\frac {1}{2}}(I_{yy}-I_{zz})\cdot \sin(2\cdot \phi )+I_{yz}\cdot \cos(2\cdot \phi )}$,

Angle to the main axis of inertia:

${\displaystyle \phi ^{*}={\frac {1}{2}}\cdot \arctan {\frac {-2\cdot I_{yz}}{(I_{yy}-I_{zz})}}}$

With the help of these formulas, the associated moments of inertia of a surface can be calculated if the coordinate axes of the surface are rotated by any angle . When rotating around the angle , and become extremal and . Reference axes that are described by the angle are called main axes of inertia. Since no reliable calculating machines were available in earlier years , a graphic method was specified by Christian Otto Mohr . The Mohr's circle of inertia can still be found in many textbooks on technical mechanics . The twisted geometrical moments of inertia are used in practice in the calculation of stresses when the loading bending moment does not fall in the direction of one of the two main moments of inertia during bending . ${\displaystyle \phi }$ ${\displaystyle \phi ^{*}}$ ${\displaystyle I_{\eta \eta }}$ ${\displaystyle I_{\xi \xi }}$ ${\displaystyle I_{\eta \xi }=0}$ ${\displaystyle \phi ^{*}}$

Derived quantities

Moment of resistance

The modulus can be used in the linear elasticity theory, the occurring at the cross-sectional edge largest stress ( voltage ) to be determined. It is the quotient of the area moment of inertia and the distance between the edge and the neutral fiber : ${\displaystyle W}$ ${\displaystyle a_{\max }}$

${\displaystyle W:={\frac {I}{a_{\max }}}}$

Area Radius of Inertia

For geometrically similar components (e.g. rectangles with the same width / height ratio), the area radius of inertia can also be defined with the dimension length , with which one can compare bodies that are similar in terms of the second degree moment of area:

${\displaystyle i_{y}:={\sqrt {I_{y} \over A}};\qquad i_{z}:={\sqrt {I_{z} \over A}}}$

${\displaystyle i_{P}:={\sqrt {I_{P} \over A}}}$

The area radius of gyration is often referred to as the " gyration radius ", but there is a risk of confusion with the radius of the scattering mass. In addition, the area radius of inertia is included in the slenderness ratio . ${\displaystyle \lambda }$

Area stiffness / area stiffness

The rarely used surface stiffness (no formula symbol), also called surface stiffness, is the square of the radius of gyration or the quotient of the area moment of inertia and the cross-sectional area:

${\displaystyle \mathrm {Fl{\ddot {a}}chensteife} =i^{2}={\frac {I}{A}}}$

Both surface stiffness and surface inertia radius should be as large as possible for good material utilization. However, this leads to ever larger, thinner-walled objects, which are then increasingly at risk of buckling .

Examples

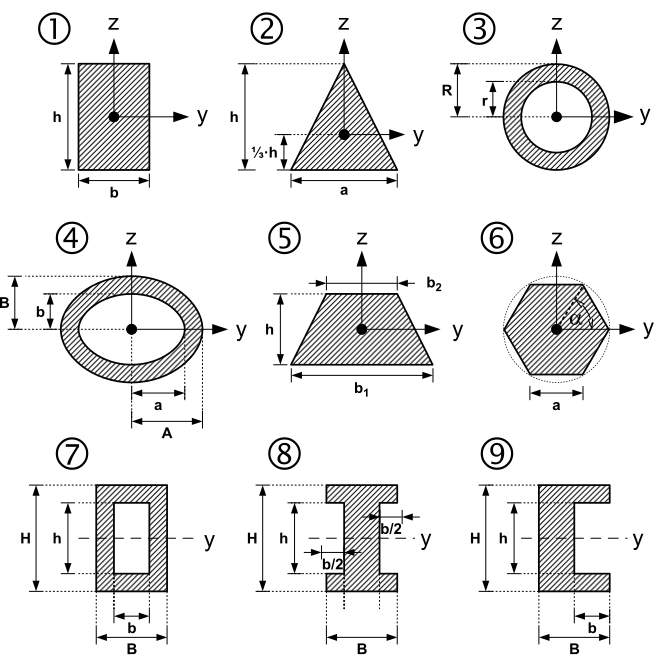
The polar moment of inertia of the 2nd degree is provided that the reference point of the polar area moment lies at the intersection of the y and z axes. ${\displaystyle I_{p}=I_{y}+I_{z}}$

No.	surface	Axial moment of area of ​​the 2nd degree		Remarks
		around y-axis	around z-axis
1: rectangle	${\displaystyle A={b\cdot h}}$	${\displaystyle I_{y}={b\cdot h^{3} \over 12}=A\cdot {\frac {h^{2}}{12}}}$	${\displaystyle I_{z}={h\cdot b^{3} \over 12}=A\cdot {\frac {b^{2}}{12}}}$	The square is a special case of the rectangle are calculated ${\displaystyle b=h}$
2: triangle	${\displaystyle A={\frac {a\cdot h}{2}}}$	${\displaystyle I_{y}={\frac {a\cdot h^{3}}{36}}={\frac {A\cdot h^{2}}{18}}}$	${\displaystyle I_{z}={\frac {h\cdot a^{3}}{48}}={\frac {A\cdot a^{2}}{24}}}$	The isosceles triangle drawn above is generally only symmetrical about the z-axis
3: circular ring	${\displaystyle A=\pi \cdot (R^{2}-r^{2})}$	${\displaystyle I_{y}=I_{z}={\pi \over 4}\cdot (R^{4}-r^{4})={A \over 4}\cdot (R^{2}+r^{2})}$		The circle can be calculated as a special case of the annulus . ${\displaystyle r=0}$
4: elliptical ring	${\displaystyle A=\pi \cdot (A\cdot B-a\cdot b)}$	${\displaystyle I_{y}={\frac {\pi }{4}}\cdot (A\cdot B^{3}-a\cdot b^{3})}$	${\displaystyle I_{z}={\frac {\pi }{4}}\cdot (A^{3}\cdot B-a^{3}\cdot b)}$	The ratio is the ratio of the half axes of the elliptical ring and must be the same as the ratio of the ellipse on the outer edge when calculating the polar area moment for the ellipse on the inner edge. ${\displaystyle n=A/B=a/b\geq 1}$ The ellipse can be viewed as a special case of the elliptical ring . ${\displaystyle a=b=0}$
5: Symmetrical trapezoid	${\displaystyle A=(b_{1}+b_{2})\cdot {\frac {h}{2}}}$	${\displaystyle I_{y}=h^{3}\cdot {\frac {(b_{1}+b_{2})^{2}+2\cdot b_{1}\cdot b_{2}}{36\cdot (b_{1}+b_{2})}}}$	${\displaystyle I_{z}={\frac {h}{48}}\cdot (b_{1}+b_{2})\cdot (b_{1}^{2}+b_{2}^{2})}$
6: Regular n-corner	${\displaystyle A={\frac {n\cdot a^{2}}{4\cdot \tan {\frac {\pi }{n}}}}}$	${\displaystyle I_{y}={\frac {n}{96}}\cdot a^{4}\cdot {\frac {2+\cos \alpha }{(1-\cos \alpha )^{2}}}\cdot \sin \alpha }$		${\displaystyle I_{y}}$ is the same around all axes
7: Box profile	${\displaystyle A=H\cdot B-h\cdot b}$	${\displaystyle I_{y}={\frac {1}{12}}\cdot (B\cdot H^{3}-b\cdot h^{3})}$	${\displaystyle I_{z}={\frac {1}{12}}\cdot (B^{3}\cdot H-b^{3}\cdot h)}$
8: I-beam (Double T-beam)			${\displaystyle I_{z}={\frac {\left({H-h}\right)\cdot B^{3}+h\cdot \left({B-b}\right)^{3}}{12}}}$
9: U-profile			${\displaystyle I_{z}={\frac {(B-b)^{3}\cdot h+B^{3}\cdot (H-h)}{3}}-{\frac {[(B-b)^{2}\cdot h+B^{2}\cdot (H-h)]^{2}}{4\cdot [(B-b)\cdot h+B\cdot (H-h)]}}}$	For the special case with the same wall thickness results . ${\displaystyle t}$ ${\displaystyle I_{z}={\frac {b^{3}\cdot t}{6}}+{\frac {H\cdot t^{3}}{12}}+{\frac {B^{2}\cdot H\cdot b\cdot t^{2}}{2\cdot (2\cdot b\cdot t+H\cdot t)}}}$

Further examples from the lexicon of all technology :

• 
• 
• 

Example calculated: Area moment of inertia of a circle with radius R

sketch

${\displaystyle I_{p}=\int \limits _{A}r^{2}\cdot dA=}$

${\displaystyle =\int \limits _{0}^{R}r^{2}\cdot 2\cdot \pi \cdot r\cdot dr=}$

${\displaystyle =2\cdot \pi \cdot \int \limits _{0}^{R}r^{3}\cdot dr=2\cdot \pi \cdot \left.{\frac {r^{4}}{4}}\right|_{0}^{R}={\frac {\pi }{2}}\cdot R^{4}}$

The following applies to the circle: In general, the following applies: The axial geometrical moment of inertia of a circle is: ${\displaystyle I_{x}=I_{y}}$
${\displaystyle I_{p}=I_{x}+I_{y}}$

${\displaystyle I_{x}=I_{y}={\frac {I_{p}}{2}}={\frac {\pi }{4}}\cdot R^{4}}$

Calculated example: area moment of inertia of a rectangle

Rectangle with height h and width b

${\displaystyle {\begin{aligned}I_{y}&=\int _{A}z^{2}\,\mathrm {dA} =\int _{-{\frac {b}{2}}}^{\frac {b}{2}}\int _{-{\frac {h}{2}}}^{\frac {h}{2}}z^{2}\,\mathrm {dz\,dy} =b\,{\frac {z^{3}}{3}}\,\,|_{(-{\frac {h}{2}})}^{\frac {h}{2}}={\frac {b}{3}}\left({\frac {h^{3}}{2^{3}}}-\left(-{\frac {h^{3}}{2^{3}}}\right)\right)={\frac {h^{3}b}{12}}\end{aligned}}}$

Moment (integration)

In the natural sciences and technology, moments are parameters of a distribution that describe the position and form of this distribution. They are calculated by integrating the distribution weighted with a power of the distance. In this sense, the geometrical moment of inertia is related to the mass moment of inertia .

Individual evidence

1. ↑ Technical mechanics for dummies, publisher: Wiley-VCH Verlag GmbH & Co. KGaA; ISBN 3527707565
2. ↑ Entry in Maschinenbau-Wissen.de
3. ↑ Torsion (mechanics) #Torsion without warping
4. ↑ Steger, Carsten (1996). "On the Calculation of Arbitrary Moments of Polygons" (PDF).
5. ↑ Schneider construction tables . 20th edition. Werner Verlag.
6. ↑ Hans Albert Richard, Manuela Sanders: Technical Mechanics. Strength theory (=  study ). Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8348-0454-9 , doi : 10.1007 / 978-3-8348-9514-1 .

Web links

Commons : Moments of Area  - Collection of images, videos and audio files

• Online calculation of area moments of inertia and resistance moments