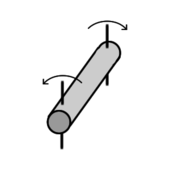
Torsion (mechanics)
The twist describes the rotation of a body by the action of a torsional moment arises. If you try to twist a rod with a lever perpendicular to the longitudinal axis, a torsional moment acts on it (in addition to any transverse force ).
The torsional moment results from the force on the lever multiplied by the length of the lever used:
The resulting twist (twist angle ) of the rod results as:
With
- the torsional moment
- the moment of direction
- the rod length
- the shear modulus
- the torsional moment of inertia , which describes the size and shape of the rod cross-section.
Torsional moment of inertia
The torsional moment of inertia is equal to the polar area moment of inertia only for circular and closed circular ring cross- sections :
For other cross-sections, the calculation of the torsional moment of inertia is only possible in closed form in special cases .
In addition, when determining the torsional moment of inertia, it is often important whether the cross-sections are warp- free or not, and whether the warping is hindered or not.
Torsion without warping
In the case of closed profiles , the products of the wall thickness and the distance to the axis of rotation being constant on each side ( ), shear stresses arise in the case of torsion , but no normal stresses in the longitudinal direction and therefore no warping of the cross-section. A cylindrical tube of constant wall thickness , for example, fulfills these conditions . This case of torsion is known as the Neubersche shell .
It should be noted, however, that the linear elasticity theory applies, i.e. H. only small distortions and deformations , but no plastic deformations are permitted. In addition, the load in the form of the torsional moment should be applied to the longitudinal axis.
The shear stress in the rod results from the torsional moment divided by the polar moment of resistance :
The maximum shear stress occurs at the edge or at the maximum radius of the cross-section under consideration. When dimensioning , it must be ensured that this shear stress does not exceed the maximum permissible shear stress of the material to be used :
Otherwise, the deformation of a wave, for example, passes from the elastic range to the plastic range and ultimately leads to breakage .
Torsion with unobstructed arching (Saint-Venant)
Pure torsion, also known as Saint-Venant's torsion, allows unimpeded displacement of cross-sectional points in the longitudinal direction (Z-direction) of the profile. One also speaks of an unobstructed curvature of the cross-section. The cross-sectional shape perpendicular to the Z direction is retained (small deformations). It is assumed that the cross-section warping is independent of the position of the cross-section and can be adjusted freely. A trick is practically used to twist profiles that do not have a circular cross-section. These can not be regarded as Neubersche bowls. However, such a profile must not be firmly clamped , it must stand freely in the space, and the moment is applied on both sides. This ensures that no normal stresses occur along the profile, although individual points on the profile may shift in the longitudinal direction.
The internal torsional moment is constant over the length of the rod and is the same as the external torsional moment. One also speaks of the primary torsional moment .
The greatest torsional shear stress is found in the area of the smallest wall thickness (theory about thin-walled closed hollow profiles and thin-walled open profiles).
Warping torsion
Warping torsion occurs in the following cases:
- if the curvature of the twisted rod cross-section is hindered at support points , for example by end plates.
- due to changes in cross-section and thus variable torsional stiffness and changing unit warpage of the rod.
- due to variable torsional load, if the resulting torsional moment in the bar is not constant (e.g. due to a section torsional moment).
- if there is no arch-free cross-section
- when a cross-section free from arching is warped by forcing another axis of rotation than its center of shear.
- when the torsional moment acts within the rod length.
Warping torsion corresponds to a local stress state that hinders the twisting of the rod due to a support condition. Mathematically one can imagine the warping torsion as a St. Venant torsion with additional statically indeterminate longitudinal stresses in the support point, which must be so large that the support condition, e.g. B. longitudinal displacement equal to zero, are met.
The internal moment of the rod is then split into two parts: one comes from the pure torsion, the second from the hindered arching.
- In the case of full cross-sections, the portion of the cambering moment is usually small due to the relatively low camber, so it can usually be disregarded.
- In the case of thin-walled profiles, however, the warping torsion must be taken into account. Here occur in addition to the Saint-Venant shear stresses (primary Torsionsschubspannungen) in addition secondary thrust (also called Wölbschubspannungen) and camber-changing normal voltages on.
- In the case of closed, thin-walled profiles such as cold-formed hollow profiles, however, the warping stresses and the resulting deformations usually remain small compared to the stresses from pure torsion, which is why there is generally no need to consider the warping torsion. However, borderline cases must be considered that take into account the cross-sectional deformations in the case of very thin-walled cross-sections.
The twist is not constant over the length of the rod, since the influence of the arching force torsion decreases with increasing distance from the support point at which the arching of the cross section is hindered. Therefore, the normal warping stresses are not constant over the length of the bar, but they are over the cross-section.
Torsion on thin-walled profiles

Since the shear stresses caused by torsion are lower in the middle of a cross-section than towards the edge, it makes sense, according to the principles of lightweight construction , to put more material on the edge of a cross-section. This principle is used for torque transmission through shafts in the form of the hollow shaft .
In the case of thin-walled cross-sections, shear flow occurs tangentially to the wall of the pipe or shaft in question. The thrust flow is determined by:
It is
- the shear stress at the profile centerline of the cross-section
- the wall thickness of the cross-section, which can vary over the location.
The 1st Bredt formula is linked to the torsional moment:
This is the area that is enclosed by the profile center line.
Inserting Bredt's first formula into the equation for the thrust flow results in
If the profile center line is described with a running coordinate , the angle of rotation of the profile can be determined:
It is
- the length of the twisted rod
- the shear modulus .
The maximum shear stress is determined by
with the torsional moment of inertia .
If the torsional moment of inertia and wall thickness are combined to form the torsional resistance moment , then the following applies
- .
In the case of thin-walled cross-sections, it plays a major role whether the cross-section is closed or open. Closed cross-sections are significantly more resistant to torsion than open cross-sections. For example, if you look at the closed cross-section of a round tube, the wall thickness of which is 10% of its radius, and compare it with a slotted cross-section with otherwise the same properties, the torsional moment of inertia and consequently the moment to be applied for a certain angle of rotation are greater by a factor of 300 for the closed cross-section.
Applications
The effect of torsion is used in many areas:
- Torsional pendulum as a time standard in clocks
- Henry Cavendish used a gravitational balance in 1798 to measure the gravitational constant . A balance was established between the torsional force of the suspension wire and the gravitational force.
- Coil spring
- Torsion bar spring in vehicle construction
- Torsion gun, antique artillery weapon
- Torsion test for material testing
- Spanish winch for tensioning
- Wring out (pre-drying) laundry, mop or hair, for example
literature
- Wolfgang Francke and Harald Friemann: Shear and torsion in straight bars: Basics and calculation examples . Vieweg, Konstanz 2005, ISBN 3-528-03990-6 .
- Edmund Spitzenberger: Warping torsion of mixed open-closed cross-sections . VDM, Saarbrücken 2008, ISBN 978-3-639-02493-7 .
- Karl-Eugen Kurrer : History of Structural Analysis. In search of balance , Ernst and Son, Berlin 2016, pp. 542–557, pp. 573f and pp. 585–588, ISBN 978-3-433-03134-6 .
Individual evidence
- ↑ http://www.bau.uni-siegen.de/subdomains/baustatik/lehre/tm/tm2/arbeitsblaetter/torsion.pdf
- ↑ Russel C. Hibbeler: Technische Mechanik 2 Strength Theory , 8th Edition, Pearson Germany, Munich 2013, ISBN 978-3-86894-126-5 .
- ↑ Bernd Markert : Mechanics 2 Elastostatics - Statics of deformable bodies , 2nd edition, Institute for General Mechanics Aachen , Aachen 2015.
Web links
- Torsion (mechanics) (calculator English)
- Video: torsional deformation of metals . Institute for Scientific Film (IWF) 1974, made available by the Technical Information Library (TIB), doi : 10.3203 / IWF / E-1899 .
- Video: Torsional stress - inhomogeneities in the deformation of steel, copper and aluminum alloys . Institute for Scientific Film (IWF) 1978, made available by the Technical Information Library (TIB), doi : 10.3203 / IWF / E-2440 .