Gravitational constant

Physical constant
Surname	Gravitational constant
Formula symbol	${\displaystyle G}$
value
SI	6th.67430 (15)e-11 ${\displaystyle \textstyle {\frac {\mathrm {m^{3}} }{\mathrm {kg\,s^{2}} }}}$
Uncertainty  (rel.)	2.2e-5
Planck units	1. Occasionally, however, 1 is also set. ${\displaystyle 8\pi \;G}$
Sources and Notes
Source SI value: CODATA 2018 ( direct link )

The gravitation constant (symbol or ) is the fundamental natural constant that determines the strength of gravity . In the law of gravitation by Isaac Newton it directly gives the strength of the gravitational force between two bodies in function of their spacing and their masses , in the general theory of relativity by Albert Einstein , it determines the curvature of the four-dimensional space-time , and thus the flow of all phenomena associated with the gravity. It is of fundamental importance for the description of astronomical quantities and processes. The value of the gravitational constant is ${\displaystyle G}$ ${\displaystyle \gamma }$

${\displaystyle G=(6{,}674\,30\pm 0{,}000\,15)\cdot 10^{-11}\,\mathrm {\frac {m^{3}}{kg\cdot s^{2}}} ,}$

whereby the fourth decimal place is already uncertain.

definition

According to Newton's law of gravity , two spherically symmetrical bodies with the masses and , whose centers are spaced apart , pull each other with the force ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$ ${\displaystyle r}$

${\displaystyle F=G\,{\frac {m_{1}\,m_{2}}{r^{2}}}}$

on. The constant of proportionality appearing in the equation is the constant of gravity. ${\displaystyle G}$

This form of law was introduced in 1873, 200 years after Newton, by Alfred Cornu and Jean-Baptist Baille . Newton wrote his law without naming the constant in the form of proportionalities , as was common in scientific literature at the time. ${\displaystyle F\propto m_{1}\ ,\ F\propto m_{2}\ ,\ F\propto r^{-2}}$

Value and units

In the International System of Units (SI) the value according to the current recommendation CODATA  2018 is:

${\displaystyle G=6{,}674\,30(15)\cdot 10^{-11}\,\mathrm {\frac {m^{3}}{kg\cdot s^{2}}} }$

(i.e. with an estimated standard uncertainty of ). ${\displaystyle 0{,}000\,15\cdot 10^{-11}\,\mathrm {m} ^{3}/(\mathrm {kg} \cdot \mathrm {s} ^{2})}$

In the CGS system of units has the value ${\displaystyle G}$

${\displaystyle G=6{,}674\,30(15)\cdot 10^{-8}\,\mathrm {\frac {cm^{3}}{g\cdot s^{2}}} .}$

The gravitational constant can also be expressed with other natural constants, for example with the help of Planck's reduced quantum of action and the speed of light (" natural units "). According to CODATA 2018, the value is: ${\displaystyle \hbar }$ ${\displaystyle c}$

${\displaystyle G=6{,}708\,83(15)\cdot 10^{-39}\,{\frac {\hbar c}{(\mathrm {GeV} /c^{2})^{2}}}}$

Compared to other basic forces in physics , gravitation is a very weak interaction, which is expressed in the small value of the gravitational constant. For example, if you calculate the absolute value of the ratio between the gravitational force and the electrostatic force between two protons , you get, regardless of the distance:

${\displaystyle \left|{\frac {F_{\text{Gravitation}}}{F_{\text{elektrisch}}}}\right|={\frac {Gm_{\text{Proton}}^{2}}{e^{2}/(4\pi \varepsilon _{0})}}\approx 10^{-36}}$

Measurements

The gravitational force between the earth and another object, i.e. In other words , its weight can be measured very precisely, but in order to determine the gravitational constant with the same accuracy, one would have to know reliably the earth's mass or, better yet, the entire mass distribution in the earth. However, this is not the case, so that the extremely low force of attraction between bodies of known mass must be determined in the laboratory to measure . For example, the force of attraction between two bodies of 100 kg each at a distance of 1 m is less than 10 ⁻⁹ (one billionth) of their weight, and all other matter in the laboratory or outside of it also exerts gravity on the test body. These measurements are therefore difficult. Even the smallest temperature differences, air currents, irregularities in the material or creeping of the material, even the number of vehicles in the parking lot in front of the institute building, falsify the results. ${\displaystyle G}$

Current status

A value for with eight-digit accuracy, as has long been achieved for other natural constants, would require a reduction of such possible interfering influences to 10 ⁻¹⁷ (one hundred billionth) of the weight of the bodies involved. So far this has not been successful. Five-digit accuracy is therefore the highest, it was specified for a measurement from the year 2000. However, from the last three decades alone there have been a total of 13 other measurement results from laboratories around the world with various devices, e.g. Some indicate a similarly high level of accuracy, but still differ by almost ten times the specified uncertainty ranges. It is assumed that the individual devices have undetected weak points. ${\displaystyle G}$ ${\displaystyle G}$

As a result, the relative uncertainty of the current value cannot be suppressed below 2.2 · 10 ⁻⁵ . This means that the fundamental constants of nature are currently the one with the lowest measurement accuracy. For comparison: The Rydberg constant is known in SI units with a relative uncertainty of 1.9 · 10 ⁻¹² , which is more than a million times more accurate. ${\displaystyle G}$ ${\displaystyle G}$

The - in comparison - low accuracy of and the excessive spread of the individual results are considered deficiencies. In addition to undetected weak points in the measuring equipment, the spread could also indicate an aspect of gravity that has not yet been understood. The inaccuracy limits the possibility of being able to determine its mass from the gravitation of a celestial body. To do this, the celestial body must be circled by a companion whose orbit radius and orbital frequency are known so that the gravitational parameter can be determined. This is often possible with high accuracy, for the earth z. B. with up to 10-digit accuracy (see WGS 84 ). Then the mass of the celestial body results from (see Kepler's laws ). Despite the uncertainty, this is much more precise than if one estimated the mass from the diameter and the density curve inside the celestial body. ${\displaystyle G}$ ${\displaystyle r}$ ${\displaystyle \omega }$ ${\displaystyle \mu =r^{3}\omega ^{2}}$ ${\displaystyle M=\mu /G}$ ${\displaystyle G}$

In the latest experiments, the gravitational constant is measured with two different methods by varying the experimental set-up of the pendulum balance:

• Oscillation time method: A gold-plated quartz block on a glass fiber and two steel balls, each weighing 778 grams, change the torsional oscillations, resulting in a gravitational constant of ± 11.64 ppm. ${\displaystyle 6{,}674\,184\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}} }$
• Method for measuring the angular acceleration: In the second test set-up, both masses (quartz block and steel balls) can rotate independently and the turntable is tracked in such a way that the torsion is compensated, which means that no angle of rotation but the angular acceleration (" angular acceleration feedback method ") to compensate for the angle of rotation, from which a value of ± 11.61 ppm was derived. ${\displaystyle 6{,}674\,484\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}} }$

In previous experiments the standard deviation was ± 47 ppm, so it was improved by ± 36 ppm.

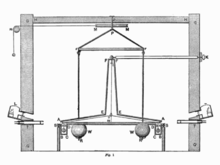
The Cavendish experiment

Cavendish experiment (1798)

Henry Cavendish succeeded in measuring the gravitational force between two masses of known magnitude for the first time in 1798 with the help of the gravitational balance he invented . The scales consisted of two spherical test masses with a total of (in today's units)  = 1.46 kg, which were connected to a dumbbell and suspended from a torsion wire so that they could carry out free horizontal torsional vibrations. Two large spheres with a total mass , equidistantly close to each of the test masses, generated the force of attraction that deflected the test masses approx. 1 ° from the rest position. The torsional force was determined from the deflection angle, which balances the force of attraction of the large and small balls at this distance. The necessary knowledge of the torsional stiffness of the wire was obtained from the period of the torsional vibration. ${\displaystyle m}$ ${\displaystyle M_{c}=316\,\mathrm {kg} }$ ${\displaystyle r_{m}}$ ${\displaystyle F_{c}}$

The formula results from Cavendish's measured values

${\displaystyle {\frac {F_{c}\,r_{m}^{2}}{m\,M_{c}}}=G}$

a value for the constant

${\displaystyle G_{\mathrm {Cavendish} }=6{,}754\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}} .}$

This falls short of today's value by only 1.2 percent.

However, the concept of a gravitational constant was not at all common in Cavendish's time, but Newton's law of gravitation was used exclusively in the form of proportionalities. Accordingly, he considered the relationship between the two forces and , with which the small spheres are attracted to the large or to the earth. According to Newton: ${\displaystyle F_{c}}$ ${\displaystyle F_{E}}$

${\displaystyle {\frac {F_{c}}{F_{E}}}={\frac {M_{c}}{M_{E}}}\ {\frac {r_{E}^{2}}{r_{m}^{2}}}}$

${\displaystyle F_{E}}$is nothing other than the (total) weight of the small balls, so that the earth's mass is the only unknown here. Cavendish was able to determine the mass of the earth from his measurement data. The physically incorrect and, strictly speaking, pointless formulation that Cavendish had "weighed the earth" became popular. ${\displaystyle M_{E}}$

After the earth's mass, implicitly the value of the gravitational constant, was known, the masses of other celestial bodies in the solar system could also be determined.

See also

• Gaussian constant of gravity

literature

• Venzo de Sabbata: The gravitational constant - generalized gravitational theories and experiments. Kluwer Academic, Dordrecht 2004, ISBN 1-4020-1955-6 .
• Achim Schumacher: Systematic investigations into the measurement of Newton's gravitational constants with a pendulum resonator. (PDF; 3.89 MB) August 1999, accessed on November 18, 2009 (dissertation (University of Wuppertal)). 

Web links

Wiktionary: gravitational constant  - explanations of meanings, word origins, synonyms, translations

• Frank Grotelüschen: gravitational constant. The severity of gravity . Deutschlandfunk.de , September 28, 2014.
• Manfred Lindinger: Gravity put to the test . Frankfurter Allgemeine Zeitung , September 13, 2018.

Individual evidence

1. ↑ ^{a b} CODATA Recommended Values. National Institute of Standards and Technology, accessed May 20, 2019 .  Value for the gravitational constant.
2. ^ ^{A b} Clive Speake, Terry Quinn: The search for Newton's constant . In: Physics Today . tape 67 , no. 7 , 2014, p. 27 , doi : 10.1063 / PT.3.2447 .
3. ↑ CODATA Recommended Values. National Institute of Standards and Technology, accessed May 20, 2019 .  Value for the gravitational constant in natural units. The numbers in brackets denote the uncertainty in the last digits of the value; this uncertainty is given as the estimated standard deviation of the specified numerical value from the actual value.
4. ^ David F. Bartlett: Why is it so easy to underestimate systematic errors when measuring G? Phil. Trans. R. Soc. A 372, 2014, doi: 10.1098 / rsta.2014.0021 (free full text).
5. ↑ [1] Nature 29 August 2018: Measurements of the gravitational constant using two independent methods
6. ↑ [2] FAZ, updated on September 13, 2018: Gravity on the test bench
7. ^ Henry Cavendish: Experiments to Determine the Density of the Earth. (PDF) 1798 (English).