Buckling

In technical mechanics, buckling is understood as the (sudden) loss of stability of bars due to lateral deflection under axial compressive stress . Buckling occurs when the rod reaches the compressive stress at which it loses its stable equilibrium . The minimal deviations from the completely symmetrical loading and uniform shape of the rod, which are always present in practice, initially lead to elastic bending of the rod when the load is higher . From a critical load, the rod (suddenly) gives way and deforms strongly. The critical compressive stress depends on the bending stiffness of the cross-section and the elasticity ( modulus of elasticity ) of the material. The critical compressive stress of slender bars is smaller than the bending and compressive strength of the material.
While in the case of very compact bars the material yields under too high a pressure load, bars above a certain length fail due to buckling before the maximum permissible compressive stress of the material is reached. The risk of buckling depends on:
- the introduction of the compressive force (symmetrical or asymmetrical on one side),
- the storage of the ends of the rod ( e.g. by means of a swivel joint , displaceable with a push or swivel joint or firmly clamped); see "Euler buckling cases"
- the geometry of the rod cross-section, from which the area moment of inertia results,
- the modulus of elasticity of the material from which the rod is made.
One distinguishes
- Flexural buckling (lateral deflection of the bar axis),
- Torsional buckling (twisting of the bar cross-section) and
- Torsional torsional buckling (twisting of a bar cross-section while simultaneously giving way to the side).
This article only deals with the buckling of a rod-shaped component under compressive force. If buckling is calculated with a constant modulus of elasticity, then this calculation only applies to elastic behavior. The former is commonly referred to as "kinking" in everyday life.
Euler buckling cases (flexural buckling)
After Leonhard Euler , who was the first to deal with the buckling of slender rods, four cases are named for buckling of the elastic rod with centrally acting compressive force. These four Euler cases are not the only ones that occur in building practice and machine technology. There are missing z. B. the cases when the rod is guided vertically at the top, but can move sideways. The rod, which is additionally clamped at the bottom, is a useful model for columns in a skeleton construction and corresponds numerically to the Euler case (2). Furthermore, there is a lack of elastically embedded rods (e.g. piles) as well as torsion spring models, which practically always prevail in reality, since as a rule neither ideal fixtures nor ideal joints can be produced.
Euler investigated the balance of stresses on already deformed bars, this approach was new for its time and led to extensive knowledge within the stability theory .
The second Euler case
Euler's buckling cases apply to members with a constant cross-section over the entire length. For each of these cases he determined the critical compressive force which, if exceeded, causes buckling. There are different ways of deriving this. The following derivation for the so-called Euler case (2) has the advantage of being particularly clear.
The ideal buckling compressive load according to the second order theory is independent of the selected pre-deformation. With the bending moment from the compressive force and the maximum deflection , the resulting additional deflection can be calculated using the differential equation of the elastic line . This results in a further additional bending moment and the further additional bending . The process is repeated an infinite number of times. The total deflection is
- + ....
Let the following deflection be (with i≥1).
So follows
- .
Since the following bend is similar to the previous bend (sinusoidal), it can be written:
- = ...,
and with
- .
This geometric series converges. Their total value is finite. In other words, if , the end deflection has a finite value. At the rod buckles.
- is called the buckling condition .
The critical pressure force or the Euler force is calculated as follows:
Equation for assumed initial bending line:
- .
Differential equation for :
- ( : Modulus of elasticity ; : axial area moment of inertia of the cross section)
After two integration (boundary conditions , if or ) and substitutions:
- .
- .
If so , then the critical compressive force is:
- .
The Euler cases (1) and (4)
In these two Euler cases, the sinusoidally assumed bending lines are other sections of an entire sinusoidal line (see figure above), which is why their equations follow directly from that for case (2):
(2): half sine wave length >> length , ,
(1): fourth Cosinuswellenlänge >> length , ,
(4): entire length Cosinuswellenlänge >> , .
is called the buckling length coefficient and the buckling length .
The other critical compressive forces are:
- (1):
- (4):
The third Euler case
- (3):
other sizes
The slenderness is used as a further variable :
where stands for the radius of gyration of the cross section.
Furthermore, the buckling stress results from:
The function results in a second- degree hyperbola , the so-called Euler hyperbola . Divided by the modulus of elasticity results in the buckling strain , a quantity that only depends on the geometry (length, cross-sectional shape and size, bearing).
Inelastic buckling according to Tetmajer

In the case of compact rods, below a limit slenderness, there is an area of kinking that is no longer characterized solely by the elasticity of the material. For a structural steel with the designation S235JR (S235JRG2 - old designation: St37) the limit for is 105. Similar limit values are given for other materials .
The slimness limit can also be calculated. It results in:
- ,
when the proportional limit of the material of the pressed rod is.
Below this slenderness limit, the Tetmajer equations are valid. These are numerical equations that have slenderness as an independent variable in the function . They have the following structure:
The coefficients for the Tetmajer equation can be taken from the following table for the most common building materials:
| material | Coefficient a | Coefficient b | Coefficient c |
|---|---|---|---|
| Softwood | 29.3 | -0.194 | 0.000 |
| Cast iron (gray cast iron) | 776.0 | -12,000 | 0.053 |
| Structural steel S235JRG2 (St37) | 310.0 | -1.140 | 0.000 |
| Structural steel S355J2G3 (St52) | 335.0 | -0.620 | 0.000 |
Uniaxial or biaxial flexural buckling
Let it be the rod or beam axis and the main axes of inertia of the (non-twisted) cross-section. Then - if the boundary conditions allow it - the member axis gives way
- only in the xη-plane (uniaxial buckling, generally decisive) or
- only in the xζ-plane (uniaxial buckling, generally decisive) or
- in both planes at the same time (biaxial buckling)
possible. The latter option is particularly important when buckling loads for uniaxial buckling are not far apart in the two planes. A separate treatment of the two uniaxial buckling processes is then not possible, because influences of non-linear material behavior cause a coupling. It should be noted that for buckling, curvatures ( ) (e.g. due to loading ( bending moment , temperature differences), pre-deformations (e.g. pre-twisting or pre-bending) as well as other imperfections and transverse loads (M, Q, q)) mainly affect the Impact stability risk and it can therefore lead to girders buckling around the major axis (e.g. rafters of a roof structure).
Buckling under axial inertia forces

Buckling under axial inertia forces, e.g. B. the dead weight or with high axial acceleration is a stability case that cannot be calculated with the approaches handed down by Euler or Tetmajer. The combinatorial variation of the possible bearings results in seven different buckling cases. In the case of cylindrical bars, such buckling problems lead to Bessel differential equations , the solutions of which have to be determined numerically with the help of tabulated Bessel functions. A classic example of this problem are the chimneys of large coal-fired power plants . The determination of the geometrical moments of inertia required for such a case can be carried out using the Ritz method . Nowadays it is often pushed out of practice by the finite element method .
Torsional buckling and torsional torsional buckling
Pure torsional buckling (twisting of the bar with the bar axis unchanged) is generally not of practical interest because the bar axis usually yields even with lower loads.
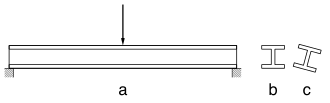
a) view (without deformation drawn)
b) cross-section in the vicinity of the Auflagers
twisted c) due Biegedrillknickens cross-section in the middle of carrier
In contrast, the stability of a girder is under certain circumstances endangered by torsional torsional buckling even if no compressive forces are present. The picture shows an example, an older term for the failure of a beam subject to bending stress due to torsional torsional buckling is tilting.
The resistance to torsional torsional buckling is influenced not only by the influences listed above, but also by the torsional stiffness and the torsion-preventing support of the beam.
Mathematical models of the buckling problem
The differential equation of the buckling problem can be obtained by formulating the equilibrium conditions on the deformed rod or beam (second order theory, see structural analysis ).
If the differential equation for a straight, unrestricted elastic rod is linearized with central load application, then mathematically this leads to an eigenvalue problem . At the first eigenvalue, the solution of the differential equation branches out, the limit of stability is reached (black horizontal line). If the linearization of the differential equation is omitted, it becomes apparent that a (small) increase in load can still be achieved with rapidly increasing deformation (dashed black line).
If the (unavoidable) imperfections (pre-deformations of the bar axis, irregularities in the material, residual stresses , eccentricity of the load transfer) are taken into account, an inhomogeneous differential equation (no eigenvalue problem) arises. The deformations increase sharply even before the critical load is reached. If the differential equation has been linearized, the curve approaches the branching load asymptotically (red curve). The prerequisite for this is that the material remains in the purely elastic range and the rods are slim.
In the case of a partial plasticization of the cross-section with compact members below the branching load, this cannot be achieved (blue curve).
Buckling verification for steel rod structures that are at risk of stability
DIN EN 1993-1-1: 2010 (Eurocode 3), which has been in force since November 2010, allows three procedures:
- Calculation of the entire system according to the second order theory, whereby the imperfections to be taken into account are specified by the standard or
- Subsystems of the structure are verified with pre-warping and twisting according to the second order theory. In addition, the torsional torsional buckling analysis and the bending buckling analysis are carried out with the equivalent member method.
- Application of the "equivalent member method" for the individual members according to the first order theory. The imperfections to be taken into account are implicitly included in the calculation process.
The Omega procedure
The method was developed by the Deutsche Reichsbahn for its own steel bridges made of structural steel and was specified in DIN 4114. It provided a very simple proof of buckling resistance. Depending on the degree of slenderness , the buckling numbers were plotted in two tables for the materials S235JR + AR (St37) and S355J2 + N (St52). No proof of buckling resistance was necessary for slenderness degrees of less than 20; Slenderness levels greater than 250 were not permitted. The kink values also mentioned were between 1 and 10.55 for S235JR + AR. The proof of safety had the following form:
The value of corresponds to the permissible compressive stress for the corresponding material in the associated load case. The great advantage of the method was the fact that the buckling check was reduced to a simple stress check with compressive forces. Buckling safety factors of 1.3 to 1.5 were incorporated into the numbers .
In the event that no table of numbers is available, the numbers for the material S235JR + AR (St37) can be approximately determined using the following formula:
The process has meanwhile been replaced by other and more precise processes, but its clarity still has a certain importance in the training of engineers .
literature
- István Szabó : Introduction to Engineering Mechanics. 8th revised edition, Springer Verlag Berlin 1975, reprint 2003, ISBN 3-540-44248-0 .
- Alf Pflüger : stability problems of the elastostatics. 3rd edition, Springer Verlag Berlin 1975, ISBN 3-540-06693-4 .
- Stephen P. Timoshenko , James M. Gere: Theory of Elastic Stability. McGraw-Hill New York / Toronto / London, 2nd Ed. 1961. Reprinted Dover Publications 2009, ISBN 978-0486-47207-2 .
- Jürgen Fehlau: Introduction to DIN EN 1993 (EC 3).
- Karl-Eugen Kurrer : History of Structural Analysis. In search of balance , Ernst and Son, Berlin 2016, pp. 519–521 and pp. 588–602, ISBN 978-3-433-03134-6 .
Web links
- Online calculation for wooden supports using the Omega method
- Online calculation for buckling of bars
Individual evidence
- ↑ Kunz, Johannes: Pressure load limits of bars with low degrees of slenderness . In: Konstruktions 60 (2008) 4, pp. 94-98
- ↑ August Föppl : Lectures on technical mechanics - third volume: Strength theory , Oldenbourg publishing house, 1944, tenth section
- ^ Fritz Stüssi : Baustatik I , Birkhäuser, 1971, page 324
- ↑ FindRoot [Tan [Pi / x] - Pi / x == 0, {x, 0.67, 1}, WorkingPrecision -> 60]. In: WolframAlpha. Retrieved July 12, 2020 .
- ↑ Kunz, Johannes: Buckling under the action of axial mass forces . In: Kunststoffe 102 (2012) 9, pp. 86–89
- ↑ Willers, FA: The buckling of heavy rods. In: Z. angew. Math. Mech. 21 (1941) 1, pp. 43-51.















































![{\ sigma _ {{\ mathrm {k}}}} = a + b \ cdot \ lambda + c \ cdot {\ lambda ^ {2}}, \ qquad \ left [{\ frac {{\ mathrm N}} {{\ mathrm {mm}} ^ {2}}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8850e0ada30fcbba4d3d826cbdc94f8d7564e4b1)













