Finite element method

Visualization of an FEM simulation of the deformation of a car in an asymmetrical frontal collision

Representation of the heat distribution in a pump housing using the heat conduction equation . The “finite elements” can be seen with the element edges as black lines.

The finite element method (FEM), also known as the “ finite element method ”, is a general numerical method used for various physical tasks . The best known is the application of FEM in the strength and deformation analysis of solids with geometrically complex shapes, because here the use of classical methods (e.g. the beam theory ) proves to be too time-consuming or impossible. Logically, FEM is based on the numerical solution of a complex system of differential equations .

The computational domain (eg. As the solids) is easier in a finite number of subregions (z. B. partial body) form divided such. B. in many small cuboids or tetrahedra . They are the "finite elements". Due to their simple geometry, their physical behavior can be calculated well with known shape functions . The physical behavior of the entire body is simulated by how these elements react to the forces, loads and boundary conditions and how loads and reactions are propagated during the transition from one element to the neighboring one due to very specific problem-dependent continuity conditions that the approach functions must fulfill.

The approach functions contain parameters that usually have a physical meaning, such as B. the displacement of a certain point in the component at a certain point in time. The search for the motion function is thus reduced to the search for the values ​​of the parameters of the functions. The accuracy of the approximate solution can be improved by using more and more parameters (e.g. more and more, smaller elements) or ever higher-value approach functions.

The development of the FEM was only possible in essential stages through the development of powerful computers, as it requires considerable computing power. Therefore, this method was formulated in a computer-friendly manner from the outset. It brought a significant advance in the treatment of computational areas of any shape.

introduction

Generated structural model of a reciprocating piston (diesel engine) as a component of an internal combustion engine for the purpose of stress analysis

With the FE method, problems from different physical disciplines can be calculated, as it is basically a numerical method for solving differential equations . First, the calculation area (“component”) is divided into a large number of elements - sufficiently fine. These elements are finitely small (finite), but their actual size remains mathematically relevant - they are not "infinitely small" (infinite). The division of the area / component into a certain number of elements of finite size, which can be described with a finite number of parameters, gave the method the name "finite element method".

There are shape functions for these elements (e.g. local Ritz approaches per element) that describe how an element reacts to external influences and boundary conditions. If you insert these shape functions for all elements in the differential equations to be solved, which describe the physical laws, you get a mostly very large system of equations together with the initial, boundary and transition conditions. Solving it (at least approximately) is the task of the FE equation solver. The size of the system of equations to be solved depends largely on the number of finite elements. Its approximate solution ultimately represents the numerical solution of the differential equation under consideration; If it is solved for all elements how they behave under the loads, then this also results in the reaction of the entire component.

Finite, infinite

Mathematically, the size of each element remains relevant and must also be included in its calculation, it is just 'finitely' small. In the case of 'infinitely' small elements, their size would be negligible and would no longer be taken into account in the equations. In this regard, the element size remains relevant.

A “sufficiently fine” division of the component into elements is present if further refinement no longer has any significant influence on the calculation result. I.e. the overall result is independent of the element size, which (from this point of view) is then no longer relevant. If the element size still has a significant impact on the overall result, then i applies. A. the meshing as not fine enough.

history

The use of FEM in practice began in the 1950s with a structural calculation of aircraft wings in the aerospace industry ( Turner , Clough 1956) and very soon also in vehicle construction. The method is based on the work at Daimler AG in Stuttgart, which used the self-developed FEM program ESEM (Elastostatic Element Method) long before computer-aided design (CAD) was introduced in the early 1980s. The term finite element method was first proposed by RW Clough in 1960 and has been used everywhere since the 1970s. The most common German-language term for industrial users is calculation engineer .

The history of the finite element method emerges from the research and publications of the following authors (selection):

• Karl Heinrich Schellbach : Calculus of Variations ; Solution of a minimal area problem (1851/52)
• Ernst Gustav Kirsch: The fundamental equations of the theory of the elasticity of solid bodies, derived from the consideration of a system of points which are connected by elastic struts (1868)
• John William Strutt, 3rd Baron Rayleigh (1842-1919): On the theory of resonance. 1870
• Walter Ritz (1878–1909): new method for solving variation problems, Ritz's method (1908/09)
• Boris G. Galerkin (1871–1945): Method of Weighted Residuals (1915)
• Erich Trefftz (1926): locally limited approach functions; Counterpart to the Ritz method
• Hans Ebner (1929): Schubblech as a level element in aircraft construction
• Alexander Hrennikoff (1896–1984): Rod models, replacement of panes with trusses, panels with support grates 1940/41
• Richard Courant (1888–1972): Variational methods for the solution of problems of equilibrium and vibration (s). 1943 (approach functions with local support, element-wise approaches for vibration problems)
• William Prager (1903–1980), John Lighton Synge (1897–1995): Approximation in Elasticity based on the concept of function space. 1947
• John Argyris (1913-2004): Force and displacement method for bar structures, matrix formulation (1954/55)
• MJ Turner, Ray W. Clough , HC Martin, LJ Topp: Stiffness and deflection analysis of complex structures. 1956 (first structural calculation of airplane wings at Boeing , first application of FEM with computer program, first application of surface elements)
• Ray W. Clough (1920-2016): The finite element method in plane stress analysis. 1960 (probably first use of the term finite elements)
• Spierig (1963): Development of triangular elements, transfer to shells
• Olgierd Cecil Zienkiewicz (1921–2009), pioneer of FEM and first standard work (textbook): The Finite Element Method in Structural and Continuum Mechanics , 1967 (with YK Cheung)
• Alfred Zimmer (* 1920) and Peter Groth (* 1938), pioneers of FEM, first German FEM textbook: Element Method of Elastostatics , 1969 Oldenbourg Verlag Munich, Vienna
• Olga Alexandrovna Ladyschenskaja (1922–2004), Ivo Babuška (* 1926) and Franco Brezzi (* 1945) - Ladyschenskaja-Babuška-Brezzi condition for the stability of a mixed finite element problem with a saddle point structure
• Ivo Babuška (* 1926) - adaptive finite element algorithms

application

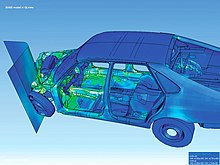
The first application of the FEM was the linear treatment of solids and structures in the form of the displacement method and based on this, the FEM received its impulses. The term “finite elements” was used a little later. In the further course of the research, the finite element method was generalized more and more and can now be used in many physical problems, u. a. can be used in various coupled field calculations, weather forecasts or for technical questions in the automotive, medical, aerospace, mechanical or consumer goods industries in engineering. One of the main areas of application of the method is product development , whereby, among other things, mechanical strength calculations of individual components or, for example, complete chassis and body structures are calculated in order to save time- consuming crash tests .

Procedure for a linear mechanical calculation (exemplary)

Programs that use the finite element method work according to the EVA principle : The user creates a (component) geometry in a CAD program. He then makes further entries in the so-called FE preprocessor . An FEM equation solver carries out the actual calculation, and the user receives the calculated results, which he can then view in the so-called FE post-processor in the form of graphic displays. Often the preprocessor and postprocessor are combined in one program or are even part of the CAD program.

Process chain linear strength calculation

Input: preprocessor

The component is designed in the CAD program and transferred to the FE preprocessor using a direct interface or a neutral exchange format such as STEP . By selecting network parameters such as element size and element type (e.g. tetrahedron, hexahedron in 3D) in the meshing module, the finite elements are generated with the help of a meshing algorithm. For the mechanical strength analysis, the material behavior must be entered, which essentially indicates which reactions the component has to external loads (e.g. deformation). Depending on the material, the relationship between tension and strain is different and there are different deformations. If this relationship is linear, only the modulus of elasticity and the Poisson's ratio are required for the FE calculation , otherwise further material parameters and inputs in the preprocessor are necessary. Further boundary conditions are, for example, loads acting on the component (forces, pressure, temperature, etc.). In order to obtain a representation that is as realistic as possible, the homogeneous (restraints) and inhomogeneous boundary conditions (displacements) as well as all loads to be taken into account on the model are specified.

Processing: equation solver

Depending on the program, a separate (stand-alone program) or an integrated equation solver is used. It calculates the simulation of how the loads, forces and boundary conditions affect the individual elements of the component, and how the forces and the effects are propagated in the component and affect neighboring elements. The calculation first provides a rough approximate solution. Further iterations improve the approximation. Most iterations are calculated until there are only the slightest changes - then the approximation has "converged" and is the result of the simulation.

Output: post processor

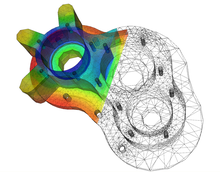
In the case of the mechanical strength calculation, the user receives the result of the FEM equation solver in particular stress , deformation and strain values . The postprocessor can display this in a false color image, for example . The equivalent stress values ​​are used, for example, to verify the strength of a component.

General functionality

Discretization

The finite element method is a discrete method; H. the solution is computed on a discrete subset of the base area. For this purpose, it is broken down into simple sub-areas, the so-called finite elements (networking, meshing). The term “finite” emphasizes the difference to the analytical consideration of infinitesimal elements. The corners of the finite elements are called nodes. These nodes form the discrete subset for the numerical method. Approximation functions are introduced on the elements, which contain the unknown node sizes as parameters. The local approximations are introduced into the weak formulation of the boundary value problem. The resulting element integrals are calculated with numerical quadrature. The approximation approaches are "integrated out" so that only the node values ​​remain on the elements as unknowns after the integration. The element equations are assembled through continuity requirements at the element boundaries. In this way, boundary value problems for linear partial differential equations are converted into a linear system of equations with symmetrical system matrices. For non-linear differential equations, the algorithm runs analogously with the difference that the non-linear dependencies are iteratively linearized using suitable methods (e.g. Newton's method) and the linear system of equations is set up for incremental quantities in each sub-step.

Example of the application of an adaptive grid to calculate the air flow around an aircraft wing.

In the case of certain tasks, the subdivision into elements is largely predetermined by the problem, for example in the case of spatial frameworks in which the individual bars form the elements of the construction. This also applies to frame constructions, where the individual beams or subdivided beam pieces represent the elements of the task. In the case of two-dimensional problems, the basic area is divided into triangles or squares. Even if only straight elements are used, a very good approximation (approximation) of the basic area can be achieved with a correspondingly fine discretization . Curvilinear elements increase the quality of the approximation. In any case, this discretization allows a flexible coverage of the basic area that is also adapted to the problem. However, care must be taken to avoid very acute or obtuse angles at the element corner nodes in order to exclude numerical difficulties. Then the given area is replaced by the area of ​​the approximating elements. The patch test can later be used to check whether it worked well.

Spatial problems are solved with a subdivision of the three-dimensional area into tetrahedral elements , cuboid elements or other elements adapted to the problem, possibly also with curved edges. d. R. Serendipity or Lagrangian elements , edited.

The delicacy of the subdivision, i. H. the density of the network has a decisive influence on the accuracy of the results of the approximation calculation. Since the computing effort increases when using finer and denser networks, it is important to develop networking solutions that are as intelligent as possible .

Element approach

In each of the elements, a problem-oriented approach is chosen for the function sought, or more generally for the functions that describe the problem. Whole rational functions in the independent space coordinates are particularly suitable for this. For one-dimensional elements (members, beams), polynomials of the first, second, third and occasionally even higher degree come into question. In the case of two-dimensional problems, linear, quadratic or higher-order polynomials are used. The type of approach depends on the one hand on the shape of the element, and on the other hand the problem to be treated can also influence the approach to be chosen. Because the approach functions have to meet very specific problem-dependent continuity conditions at the transition from one element to the next . The continuity requirements are often obvious for physical reasons and also necessary for mathematical reasons. For example, the displacement of a coherent body in one direction must be continuous when passing from one element to another in order to ensure the continuity of the material. In the case of a beam or plate bend, the continuity requirements are higher, since there, for analogous physical reasons, the continuity of the first derivative or the first two partial derivatives must be required. Elements with shape functions that satisfy the continuity conditions are called conformal.

In order to actually meet the continuity requirements, the function curve in the element must be expressed by function values ​​and also by values ​​of (partial) derivatives (the nodal point displacements) in certain points of the element, the nodal points. The function values ​​and values ​​of derivatives used in the nodes are called the node variables of the element. With the help of these node variables, the approach function is represented as a linear combination of so-called shape functions with the node variables as coefficients.

It is advisable to use a global coordinate system in addition to an element-related local coordinate system for the nodal point coordinates. Both are linked by transformation functions. If the same shape functions are used for this transformation as for the deformation approach , then they are isoparametric elements , for functions of a lower or higher degree subparametric or superparametric elements.

boundary conditions

Problem	Dirichlet boundary condition / function value	Neumann boundary condition
static problem	Support condition / displacement	force
Seepage flow	Standpipe mirror height	Source or sink
Conduction	temperature	Heat flow or heat flow density
electrical current	electrical voltage	Amperage
Electrostatics	electrical voltage	electric charge
Magnetostatics	magnetic potential	magnetic river

After a given problem has been discretized and the element matrices have been set up, given boundary conditions are introduced . A typical FE problem can have two types of boundary conditions: Dirichlet boundary conditions and Neumann boundary conditions . They always apply (work) at the nodes.

A Dirichlet boundary condition specifies a function value directly and a Neumann boundary condition specifies a derivative of a function value. If a Dirichlet boundary condition is given, this means that the problem gets one degree of freedom less and the associated row and column in the overall matrix is ​​deleted. If the Dirichlet boundary condition is not equal to zero, the value is added to the linear form ("right side") according to its prefactor. Depending on the type of physical problem, different physical quantities can be involved, as shown by way of example in the table. The Neumann boundary conditions also have a share in the linear form (“right side”).

Another variant are periodic boundary conditions , in which the values ​​at one edge are taken as data for another edge and a periodically infinitely continued area is simulated. So-called cyclic boundary conditions are defined for rotationally symmetric problems .

Basic equations of the displacement method

The displacement method is the standard formulation of the finite element method, in which the displacements are the primary unknowns that describe the translation, rotation and deformation of a solid. The displacement method is available in all common finite element programs with which problems in solid mechanics can be calculated. There are several basic equations for solving solid-state problems.

Principle of d'Alembert in the Lagrangian version

One of the equation underlying the displacement method, with which general problems of solid mechanics can be treated, is the principle of d'Alembert , as formulated in the Lagrangian description of continuum mechanics . With this principle, both linear problems, such as the question of natural vibrations, and highly non-linear problems, such as crash tests , can be analyzed. The Galerkin weighted residual method , also known as the Galerkin method or Galerkin approach, is used here.

Principle of the minimum of potential energy

In conservative systems , in the case of a static problem, the nodal displacements can be determined from the condition that the potential energy has a minimum in the desired equilibrium state . With the principle of the minimum of potential energy, the stiffness equations of finite elements can be determined directly. The potential energy of a structure is the sum of the internal strain energy (the elastic deformation energy) and the potential of the loads applied (the work done by external forces).

Arc-length method

The arc length method is a method in which one can calculate in a force-controlled manner up to the maximum load capacity. The necessity of force-controlled methods is that, in contrast to displacement-controlled methods, one can increase several loads in direct proportion. With the arc length method, the load is increased as specified; If this increase in load would lead to too great a deformation, the load is multiplied by a factor less than 1, and even with negative values ​​after the load capacity has been reached.

Stochastic finite element method

In the variant of the stochastic finite element method (SFEM), input variables of the model that are subject to an uncertainty, for example material strengths or loads, are modeled using stochastic variables. This can be achieved using ordinary random variables . Random fields are also often used, which are randomly varying, continuous mathematical functions. A common calculation method is the Monte Carlo simulation . The FE calculation is repeated for many random implementations ( samples ) of the input variables until one falls below a certain stochastic error defined in advance. Then the moments, i.e. mean value and variance, are calculated from all results. Depending on the spread of the input variables, a great number of repetitions of the FE calculation are often necessary, which can take a lot of computing time.

Implicit and explicit FE solvers

Structural mechanical FEM systems are represented by linear systems of equations of the 2nd order:

${\displaystyle M{\ddot {u}}(t)+D{\dot {u}}(t)+Ku(t)=P(t)}$

${\displaystyle M,D}$and are the mass, damping and stiffness matrix of the system; is the vector of the external forces acting on the model. is the vector of degrees of freedom. ${\displaystyle K}$ ${\displaystyle P(t)}$ ${\displaystyle u}$

Complex component models often consist of several million nodes, and each node can have up to 6 degrees of freedom. FEM solvers (equation system solvers) must therefore meet certain requirements with regard to effective memory management and, if necessary, the use of multiple CPUs. There are two fundamentally different types of FEM solvers: implicit and explicit.

Implicit FEM solvers make certain assumptions under which the calculated solution vector is valid. Acts z. B. a temporally unchangeable load on a system with damping, then after a sufficiently long time, a constant displacement vector will also be established. For is then , and the system of equations simplifies to with the solution ${\displaystyle u}$ ${\displaystyle P(t)=P=const.}$ ${\displaystyle u(t)=u=const.}$ ${\displaystyle t\to \infty }$ ${\displaystyle {\ddot {u}}(t)={\dot {u}}(t)=0}$ ${\displaystyle Ku=P}$ ${\displaystyle u=K^{-1}P}$

For a given load vector , the displacement vector can be calculated using the Gaussian algorithm or by the QR decomposition of . ${\displaystyle P}$ ${\displaystyle u}$ ${\displaystyle K}$

If a mechanical system is exposed to harmonic excitation , it may be necessary to determine the natural frequencies of the system in order to avoid resonances during operation. ${\displaystyle P(t)={\hat {P}}\sin(\Omega t)}$

Natural frequencies are all frequencies for which a displacement vector represents a solution of the unloaded ( ) and undamped ( ) system of equations. The following then applies to the velocity and acceleration vector ${\displaystyle \omega _{i}}$ ${\displaystyle u(t)={\hat {u}}_{i}\sin(\omega _{i}t)}$ ${\displaystyle P(t)=0}$ ${\displaystyle D=0}$

${\displaystyle {\dot {u}}_{i}={\hat {u}}_{i}\ \omega _{i}\cos(\omega _{i}t),\ {\ddot {u}}_{i}=-{\hat {u}}_{i}\omega _{i}^{2}\sin(\omega _{i}t)}$

and the system of equations is thus

${\displaystyle (-M\omega _{i}^{2}+K){\hat {u}}_{i}\sin(\omega _{i}t)=0}$

In order to calculate the eigenfrequencies and the associated eigenmodes , the implicit solver has to solve the eigenvalue problem ${\displaystyle \omega _{i}}$ ${\displaystyle {\hat {u}}_{i}}$

${\displaystyle -M\omega _{i}^{2}+K=0}$

to solve.

Explicit FEM solvers

Explicit solvers calculate the displacement vectors at certain discrete times within a given time interval. Node speeds and accelerations are approximated by difference quotients from the displacements at successive points in time . With a constant time step, the following applies ${\displaystyle u_{i}}$ ${\displaystyle t_{i}}$ ${\displaystyle u_{i+1},u_{i},u_{i-1}}$ ${\displaystyle t_{i+1},t_{i},t_{i-1}}$ ${\displaystyle t_{i+1}-t_{i}=\Delta \ t}$

${\displaystyle {\dot {u}}={\frac {u_{i}-u_{i-1}}{\Delta \ t}}}$

${\displaystyle {\ddot {u}}={\frac {{\frac {u_{i+1}-u_{i}}{\Delta \ t}}-{\frac {u_{i}-u_{i-1}}{\Delta \ t}}}{\Delta \ t}}={\frac {u_{i+1}-2u_{i}+u_{i-1}}{(\Delta t)^{2}}}}$

the discretized system of equations has the form

${\displaystyle M{\frac {u_{i+1}-2u_{i}+u_{i-1}}{(\Delta t)^{2}}}+D{\frac {u_{i}-u_{i-1}}{\Delta \ t}}+Ku_{i}=P_{i}}$

By solving this equation, a relationship is obtained with which the displacement vector can be determined from the vectors previously calculated and : ${\displaystyle u_{i+1}}$ ${\displaystyle u_{i}}$ ${\displaystyle u_{i-1}}$

${\displaystyle u_{i+1}=M^{-1}((\Delta t)^{2}(P_{i}-Ku_{i})-D\Delta \ t(u_{i}-u_{i-1}))+2u_{i}-u_{i-1}}$

The calculation of the inverse is not carried out in practice, since explicit solvers usually assume a diagonal matrix and therefore each line of the equation system only has to be divided by the diagonal entry in the corresponding line of . ${\displaystyle M^{-1}}$ ${\displaystyle M}$ ${\displaystyle M}$

Explicit solvers may be used. A. used in vehicle construction for the calculation of crash load cases.

The advantage of direct equation solvers according to the Gauss method lies in the practical application in the numerical stability and the receipt of an exact result. Disadvantages are the poor conditioning of the usually thinly populated stiffness matrices and the high storage requirements, as mentioned above. Iterative solvers are less sensitive to poor conditioning and require less memory if non-zero element storage is used. However, iterative solvers use a termination criterion to calculate the results. If this is achieved before an approximately exact solution has been found, the result, for example a voltage curve, can easily be misinterpreted.

In some implementations, only the positions and values ​​of the entries that deviate from zero are stored for the frequently occurring sparse matrices . This allows you to continue to solve the systems of equations directly, but saves considerable storage space.

Isogeometric analysis

→ Main article : Isogeometric analysis

Some programs can adapt an existing FE mesh to a (very similar, new) CAD geometry, which is usually significantly less than that in the event of a (minor) change in the (CAD) component geometry Computing time required.

Programs

Finite element software and its application is now a multi-billion dollar industry.

• In practice, many different stand-alone large-scale programs with a similar range of applications are in use; the selection of which program to use depends not only on the use, but also on factors such as availability, certification standard in the company or license costs.
• With the finite element packages integrated in commercial CAD systems, simpler (usually linear) problems can be calculated and then directly evaluated using the CAD system. The individual steps, e.g. B. the networking process ( meshing ) run automatically in the background.
• Since a lot of computing power is sometimes required to carry out the calculation, the first companies are making computing power available to their users in the form of cloud services.
• There are preprocessors / postprocessors with a graphical user interface and separate FE solvers.
• There are program frameworks without a graphical user interface, mostly as preprocessors with an integrated equation solver, which are operated using the programming language, for example to control the FE solver with self-made additional routines.

Mathematical derivation

The examined solution area is first divided into sub-areas , the finite elements: ${\displaystyle G}$ ${\displaystyle G_{1},\dotsc ,G_{m}\subset G}$

${\displaystyle G=\bigcup _{e=1}^{m}G_{e}}$.

Inside are the desired solution function different shape functions now defined which are only a few elements equal to zero, respectively. This property is the real reason for the term "finite" elements. ${\displaystyle G}$ ${\displaystyle f\colon G\to \mathbb {R} ^{k}}$ ${\displaystyle \psi _{1},\dotsc ,\psi _{n}\colon G\to \mathbb {R} ^{k}}$

Possible solutions of the numerical approximation are determined by a linear combination of the shape functions

${\displaystyle f(x)=\sum _{i=1}^{n}c_{i}\cdot \psi _{i}(x)\quad ,c_{i}\in \mathbb {R} }$.

Since every test function disappears on most of the elements, the function restricted to the element can, conversely , be described by the linear combination of fewer test functions . ${\displaystyle G_{e}}$ ${\displaystyle f|G_{e}}$ ${\displaystyle \psi _{i}}$

If the differential equations and the boundary conditions of the problem can be represented as linear operators with regard to the functions , this leads to a linear system of equations with regard to the free variables of the linear combination : ${\displaystyle f}$ ${\displaystyle c_{i}}$

${\displaystyle D(c)=g}$

With

${\displaystyle D}$= Linear mapping of into a functional space ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle c}$ = Vector of linear combination factors ${\displaystyle c_{i}}$

${\displaystyle g}$ = Function that represents the differential equation and the boundary conditions

In order to obtain a finite linear system of equations, the range of values ​​is also modeled using approach functions . Then the can be described using linear combinations : ${\displaystyle D}$ ${\displaystyle \phi _{1},\dotsc ,\phi _{n}}$ ${\displaystyle g}$ ${\displaystyle \phi _{i}}$

${\displaystyle g(x)=\sum _{i=1}^{n}b_{i}\cdot \phi _{i}(x)\quad ,b_{i}\in \mathbb {R} }$

and the system of equations is obtained overall

${\displaystyle A\cdot c=b}$

With

${\displaystyle A}$ = square matrix with ${\displaystyle A=\phi ^{-1}\cdot D}$

${\displaystyle c}$ = Vector of linear combination factors ${\displaystyle c_{i}}$

${\displaystyle b}$ = Vector of linear combination factors ${\displaystyle b_{i}}$

The dimension of the matrix results from the number of approach functions multiplied by the degrees of freedom on which the physical model is based . The dimension of the matrix is ​​the number of total degrees of freedom, whereby specifications corresponding to the model with regard to the uniqueness of the problem (e.g. the rigid body displacements in the case of an elastic body) must be excluded. ${\displaystyle k}$

Because each element is only connected to a few neighboring elements, most of the values ​​of the overall matrix are zero, so that it is “sparse”. In most use cases, the same functions are used as batch functions and test functions . In this case, the matrix is ​​also symmetrical about its main diagonal . ${\displaystyle \psi _{i}}$ ${\displaystyle \phi _{i}}$

If the number of degrees of freedom is not too large (up to approx. 500,000), this system of equations can be solved most efficiently using a direct method , for example with the Gaussian elimination method . The sparse structure of the equation system can be used effectively here. While the calculation effort for equations is the Gaussian algorithm , the effort can be significantly reduced by clever pivot selection (e.g. Markowitz algorithm or graph-theoretical approaches ). ${\displaystyle N}$ ${\displaystyle {\mathcal {O}}(N^{3})}$

For more than 500,000 unknowns, the poor condition of the system of equations makes the direct solvers increasingly difficult, so that for large problems, iterative solvers that improve a solution step by step are generally used. Simple examples of this are the Jacobi and Gauss-Seidel methods , but in practice multigrid methods or preconditioned Krylow subspace methods , such as the conjugate gradient or GMRES method , are used. Due to the size of the equation systems, the use of parallel computers is sometimes necessary.

If the partial differential equation is non-linear , the resulting system of equations is also non-linear. Such a problem can usually only be solved using numerical approximation methods. An example of such a method is the Newton method , in which a linear system is solved step by step.

There are now a large number of commercial computer programs that use the finite element method.

Weak formulation

An elliptic partial differential equation can be formulated weakly; H. the problem can be expressed in a way that requires less smoothness of the solution . It does this as follows.

Given a Hilbert space , a functional (function from its dual space) , as well as a continuous and elliptical bilinear form , this is called the solution of the variation problem if ${\displaystyle H}$ ${\displaystyle f\in H':=\{g:\;H\rightarrow \mathbb {R} |\;g{\text{ ist linear und stetig}}\}}$ ${\displaystyle H}$ ${\displaystyle a(\cdot ,\cdot )}$ ${\displaystyle u\in H}$

${\displaystyle a(u,v)=f(v)\ \forall v\in H}$.

Existence and uniqueness of the solution provides the representation theorem Fréchet Riesz (for the case that the bilinear form is symmetric) or the lemma Lax-Milgram (general case). ${\displaystyle u}$ ${\displaystyle a}$

We know that the room is a Hilbert room . Based on this, the Sobolew spaces can be defined using the so-called weak derivative . ${\displaystyle L^{2}(\Omega ):=\{f:\Omega \rightarrow \mathbb {R} \ |\ \|f\|_{L^{2}}<\infty \}}$ ${\displaystyle H^{s}(\Omega )}$

The problem can be seen as a variant of a partial differential equation in one area . ${\displaystyle a(u,v)=f(v)}$ ${\displaystyle \Omega }$

The Poisson problem as an example:

${\displaystyle -\Delta u(x)=f(x)\ \forall x\in \Omega }$

${\displaystyle u(x)=0\ \forall x\in \partial \Omega }$

where here denotes the Laplace operator . A multiplication with infinitely often continuously differentiable functions results after an integration ${\displaystyle \Delta }$ ${\displaystyle \psi \in C_{0}^{\infty }(\Omega )}$

${\displaystyle \Leftrightarrow -\int _{\Omega }\Delta u\,\psi \,dx=\int _{\Omega }f\,\psi \,dx\ \forall \psi \in C_{0}^{\infty }(\Omega ).}$

A partial integration (First Green's formula ) and the zero boundary conditions for then deliver ${\displaystyle \psi }$

${\displaystyle \Leftrightarrow \int _{\Omega }\nabla u\,\nabla \psi \,dx=\int _{\Omega }f\,\psi \,dx\ \forall \psi \in C_{0}^{\infty }(\Omega )}$

Now an elliptical and continuous bilinear form is on , and the right side is a continuous linear form ${\displaystyle a(u,\psi ):=\int _{\Omega }\nabla u\,\nabla \psi \,dx}$ ${\displaystyle H_{0}^{1}(\Omega ):={\overline {C_{0}^{\infty }(\Omega )}}^{\|\cdot \|_{H^{1}}}}$ ${\displaystyle (f,\psi )_{L^{2}}=f(\psi )}$ ${\displaystyle H_{0}^{1}(\Omega )}$

If the function space / Hilbert space under consideration has a finite basis, a linear system of equations can be obtained from the formulation of variations.

For function rooms, the choice of the basis determines the efficiency of the process. The use of splines with triangulations and, in certain cases, the discrete Fourier transformation (splitting into sine and cosine) are common here.

Due to flexibility considerations regarding the geometry of the area , the following approach is usually chosen. ${\displaystyle \Omega }$

The area is discretized by dividing it into triangles and using splines associated with the vertices p to span the finite-dimensional function space. The splines meet at specified points on the triangles (where δ is the Kronecker delta ). So you can then represent a discrete function through ${\displaystyle \Omega }$ ${\displaystyle \lambda _{p}(x)}$ ${\displaystyle \Omega }$ ${\displaystyle \lambda _{p}(q)=\delta _{pq}}$ ${\displaystyle u_{h}(x)}$

${\displaystyle u_{h}(x)=\sum _{p}u_{p}\,\lambda _{p}(x)}$

with the coefficients related to the basic representation. Due to the finite basis, one no longer has to test against all , but only against all basis functions; the variation formulation is reduced to due to the linearity ${\displaystyle u_{p}}$ ${\displaystyle \psi \in H_{0}^{1}}$

${\displaystyle a(u_{h},\lambda _{q})=\sum _{p}u_{p}\,a(\lambda _{p},\lambda _{q})=(f,\lambda _{q})\ \forall q}$

So we got a system of linear equations to solve

${\displaystyle A\cdot u=f}$,

With

${\displaystyle A_{pq}=a(\lambda _{p},\lambda _{q})}$

and

${\displaystyle f_{q}=(f,\lambda _{q})}$

This result is obtained with every finite basis of the Hilbert space.

example

Formal definition of the finite element (according to Ciarlet )

A finite element is a triple , where: ${\displaystyle E=(T,\Pi ,\Sigma )}$

• ${\displaystyle T}$ is a non-empty area (e.g. triangles, squares, tetrahedra, etc.)
• ${\displaystyle \Pi }$is a finite-dimensional space of shape functions (linear, quadratic or cubic shape functions, i.e. splines; sines, etc.) shape functions ${\displaystyle \rightarrow }$
• ${\displaystyle \Sigma }$is a set of linearly independent functionals on node variables ${\displaystyle \Pi }$ ${\displaystyle \rightarrow }$

It applies to the functionals that they are associated with functions of the base:

${\displaystyle \sigma _{i}\in \Sigma :\sigma _{i}(\pi _{j})=\delta _{ij}\ \ j\in \{1,\ldots ,\dim(\Pi )\}}$

So applies to every function

${\displaystyle v\in \Pi :v(x)=\sum _{i}\sigma _{i}(x)\,\pi _{j}}$.

For sine as the basis function im is then ${\displaystyle \mathbb {(} R)^{1}}$

${\displaystyle \operatorname {span} \,\left\{\sin(x),\sin(2x),\ldots ,\sin(nx)\right\}=\Pi }$

and the functional

${\displaystyle \sigma _{i}(\psi ):=(\sin(ix),\psi )_{L^{2}}}$.

For splines, however, the point evaluation on the specified points of the triangles is enough: . ${\displaystyle \sigma _{p}(\psi ):=\psi (p)}$

S1: Linear elements on triangles

The FEM space of continuous, piecewise linear functions is defined as:

${\displaystyle S^{1}(\Omega ,T):=\left\lbrace u\in C^{0}(\Omega )\;|\;{u|}_{\Delta }(x,y)=a_{\Delta }+b_{\Delta }x+c_{\Delta }y\quad \forall \Delta \in T\right\rbrace }$,

where is an area and the triangulation of the area with triangles and denotes the restriction of the continuous function to the triangle . ${\displaystyle \Omega \subset \mathbb {R} ^{2}}$ ${\displaystyle T\subset \Omega }$ ${\displaystyle \Delta }$ ${\displaystyle {u|}_{\Delta }}$ ${\displaystyle u}$ ${\displaystyle \Delta \in T}$

P1: Linear reference element on a triangle

The reference element is defined as: ${\displaystyle {\hat {T}}}$

${\displaystyle {\hat {T}}=\left\lbrace (x,y)\in \mathbb {R} ^{2}|0<x<1\;{\text{and}}\;0<y<1-x\right\rbrace .}$

The linear elements are functions of the type: ${\displaystyle P1}$

${\displaystyle p\colon {\hat {T}}\to \mathbb {R} ,(x,y)\mapsto a+bx+cy\quad {\text{mit}}\;a,b,c\in \mathbb {R} .}$

To define the function, it is sufficient to specify the values ​​at the corner points . Therefore, all functions can be represented using basic functions : ${\displaystyle p}$ ${\displaystyle {\hat {E_{1}}}:=(0,0),{\hat {E_{2}}}:=(1,0),{\hat {E_{3}}}:=(0,1)}$ ${\displaystyle p}$ ${\displaystyle {\hat {\phi }}_{i}}$

${\displaystyle p(x,y)=\sum _{i=1}^{3}\alpha _{i}{\hat {\phi }}_{i}(x,y)\quad {\text{mit}}\;\alpha _{i}\in \mathbb {R} .}$

The basic functions are given as linear functions that are only non-zero at one corner point:

${\displaystyle {\hat {\phi }}_{i}({\hat {E_{j}}})=\delta _{i,j}\quad \forall i,j=1,2,3}$

where is the Kronecker delta function. ${\displaystyle \delta }$

Transformation of the reference element

For linking of the reference element with an arbitrary triangle (vertices: ) one uses a linear transformation : ${\displaystyle T}$ ${\displaystyle E_{1},E_{2},E_{3}}$ ${\displaystyle F_{T}}$

${\displaystyle {\begin{aligned}F_{T}&\colon {\hat {T}}\to T,\quad F(v)=B_{T}v+b_{T}\\B_{T}&:=\left(E_{2}-E_{1},E_{3}-E_{1}\right),\quad b_{T}:=E_{1}.\end{aligned}}}$

In many problems relating to partial differential equations , the scalar product of basis functions (defined on any triangle ) has to be calculated: ${\displaystyle L^{2}}$ ${\displaystyle \phi _{i}}$ ${\displaystyle T}$

${\displaystyle (\nabla \phi _{i},\nabla \phi _{j})_{L^{2}(T)}=\int _{T}\nabla \phi _{i}(x)\cdot \nabla \phi _{j}(x)dx.}$

With the help of the transformation set , the integration can be shifted to the reference element:

${\displaystyle \int _{T}\nabla \phi _{i}(x)\cdot \nabla \phi _{j}(x)dx=\int _{\hat {T}}\left(\left(DF_{T}(z)\right)^{-T}\nabla {\hat {\phi }}_{i}(z),\left(DF_{T}(z)\right)^{-T}\nabla {\hat {\phi }}_{j}(z)\right)_{\mathbb {R} ^{2}}|\det DF_{T}(z)|dz.}$

literature

• Martin Mayr / Ulrich Thalhofer: Numerical solution methods in practice: FEM-BEM-FDM . Hanser, 1993, ISBN 3-446-17061-8 , pp. 312 .
• JN Reddy: Energy Principles And Variational Methods In Applied Mechanics . 2nd Edition. John Wiley & Sons, 2002, ISBN 0-471-17985-X .
• D. Braess: Finite element theory, fast solvers and applications in elasticity theory . 4th edition. Springer, 2007, ISBN 978-3-540-72449-0 .
• Günter Müller (Ed.): FEM for practitioners . 4 volumes. Expert Verlag, Renningen.
  • Volume 1: Basics: Basic knowledge and working examples for FEM applications. 2007, ISBN 978-3-8169-2685-6 .
  • Volume 2: Structural Dynamics. 2008, ISBN 978-3-8169-2842-3 .
  • Volume 3: Temperature Fields. 2007, ISBN 978-3-8169-2714-3 .
  • Volume 4: Electrical Engineering. 2009, ISBN 978-3-8169-2841-6 .
• Klaus-Jürgen Bathe: Finite Element Methods . 2nd Edition. Springer-Verlag, 2002, ISBN 3-540-66806-3 .
• WE Gawehn: Finite Element Method . BOD Book on Demand, 2009, ISBN 978-3-8370-2497-5 (FEM basics for statics and dynamics).
• Frank Rieg, Reinhard Hackenschmidt, Bettina Alber-Laukant: Finite Element Analysis for Engineers: An easy to understand introduction . Hanser Fachbuchverlag, 2012, ISBN 978-3-446-42776-1 (application of FEM in engineering).
• René de Borst , Mike Crisfield , Joris Remmers, Clemens Verhoosel: Nonlinear finite element analysis of solids and structures , Wiley-VCH 2014
• Karl-Eugen Kurrer : The History of the Theory of Structures. Searching for Equilibrium , Ernst and Son 2018, pp. 881–914, ISBN 978-3-433-03229-9

Web links

Commons : Finite Element Method  - collection of images, videos and audio files

• History of the FEM.
• The finite element method in biomedicine, biomechanics and related areas.
• Numeric methods. (Lecture and internship).
• FU Mathiak: The finite element method (FEM). [PDF; 3.86 MB].

Individual evidence

1. ^ Karl Schellbach: Problems of the calculus of variations . In: Journal for pure and applied mathematics . tape 41 , no. 4 , 1852, p. 293-363 .
2. ↑ Ernst Gustav Kirsch: The fundamental equations of the theory of the elasticity of solid bodies, derived from the consideration of a system of points which are connected by elastic struts. In: Journal of the Association of German Engineers , Volume 7 (1868), Issue 8.
3. ^ John William Strutt: On the theory of resonance . In: Philosophical Transactions of the Royal Society of London . tape 161 , 1871, pp. 77-118 .
4. ↑ Walter Ritz: About a new method for solving certain problems of variation in mathematical physics . In: Journal for pure and applied mathematics . tape 135 , 1909, pp. 1-61 .
5. ↑ Christoph Haderer: Extension and Parameter Studies of a 1-D Stochastic Finite Element Code with Random Fields. Engineering Risk Analysis Group. Technical University of Munich, 2017.
6. ^ David Roylance: Finite Element Analysis. (PDF; 348 kB), accessed on May 10, 2017.