Monte Carlo simulation

Monte Carlo simulation or Monte Carlo study , also called MC simulation , is a method from stochastics in which a very large number of similar random experiments is the basis. The attempt is made to numerically solve problems that cannot be solved analytically or only with great effort using probability theory . The law of large numbers should be seen as the basis. The random experiments can either be carried out in real life - for example by rolling the dice - or in computer calculations in which seemingly random numbers are calculated using suitable algorithms to simulate random events , which are also referred to as pseudo- random numbers .
Stanislaw Ulam , Nicholas Metropolis and John von Neumann were among the pioneers of the Monte Carlo method in the 1940s . The basic publication is a work by Metropolis, Edward Teller , Augusta H. Teller , Marshall Rosenbluth and Arianna W. Rosenbluth from 1953.
history
Enrico Fermi had the first ideas for Monte Carlo simulations in the 1930s. These were carried out in 1946 by Stanislaw Ulam and John von Neumann, whom he therefore contacted. This happened at the time of World War II while working on a then secret project at the Los Alamos Scientific Laboratory that required a code name. In the context of the development of the first atomic bomb, it was about neutron diffusion in nuclear materials. The mathematical method of the simulation also had to be kept secret. The name Monte-Carlo was coined by Nicholas Metropolis and is related to the method as follows: Stan Ulam had an uncle who always borrowed money from relatives to play games, because “he had to go to Monte Carlo”. This is of course an allusion to the Monte-Carlo casino in the district of the same name in the city-state of Monaco .
The basic publication is a work by Nicholas Metropolis, Marshall N. Rosenbluth and his wife Arianna W. Rosenbluth, Edward Teller and his wife Augusta H. Teller, published in 1953 in the Journal of Chemical Physics. The aim was to calculate the equation of state of a two-dimensional system of rigid spheres as models of a liquid. The simulation was carried out with 224 particles and periodic boundary conditions. Each simulation consisted of up to 48 cycles, in which each particle performed one movement step. One cycle took three minutes on the MANIAC I computer at Los Alamos National Laboratory . A sampling method with weighting via the Boltzmann factor was used, the heart of the MC method in the Metropolis algorithm , whereby the idea according to Marshall Rosenbluth should have come from Teller. After Rosenbluth, he and his wife did the main work for the article (Metropolis would have mainly provided computer time) and they were the only authors who followed up the process in subsequent publications, but soon turned to other research topics (plasma physics) themselves. to.
mathematics
Mathematically, the system is a probability-weighted path in phase space (generally state space). Monte Carlo simulations are particularly suited to statistical averages in size ,
or high-dimensional integrals ( Monte Carlo integration ) such as
to calculate. should in this context be a standardized statistical weight (e.g. a Boltzmann weight ). is the value of the size in the state . The summation or integration runs over a space , i.e. the phase space of the particles in the system.
Often the space is so large that the summation cannot be carried out completely. Instead, one now creates a Markov chain of states in , the frequency of which is distributed like the given weight . Areas of the room with high weight should therefore be represented more frequently in the Markov chain than areas with low weight. (One speaks here of Importance Sampling .) If this succeeds, the expectation values can simply be calculated as the arithmetic mean of the quantity for these states of the Markov chain, i.e. as
This relationship is based on the law of large numbers. Depending on the physical system, it can be difficult to create this Markov chain. In particular, it must be ensured that the Markov chain actually covers the entire room and does not only scan part of the room. It is said: the algorithm must be ergodic .
Applications
Applications of the Monte Carlo simulation are for example:
- as an alternative to the analytical solution of problems of purely mathematical origin,
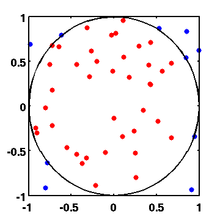
- the approximation of the number Pi with the help of Buffon's needle problem or by the random "sprinkling" of a square on the unit circle with random points (here the proportion of points that lie in the unit circle is about π / 4).
- in generalization the calculation of the integral of a function over the interval [0; 1] (area) and then also higher-dimensional integrals (volume).
- Distribution properties of random variables of unknown distribution type,
- the determination of the non-central distribution of the correlation coefficient . With the help of random numbers, the realization of any number of correlation coefficients is simulated. A summary of the coefficients in a frequency table results in an empirical distribution function .
- the properties of estimators when there are outliers in the data. With the help of the simulation it can be shown that the arithmetic mean is no longer a best estimate for the expected value .
- the estimation of distribution parameters.
- the simulation of complex processes that cannot be analyzed directly,
- Production processes in a manufacturing company to identify bottlenecks and opportunities in production
- Weather and climate of the earth.
- Reconstruction procedures in nuclear medicine .
- Risk aggregation to determine the overall scope of a company's risk in risk management
- Derivation of reviews in the valuation , eg. B. in company valuation or real estate management
- spatial distribution of the energy-dependent neutron flux in a heterogeneous medium, for example in the blanket of a nuclear fusion reactor .
Problems with statistical behavior can be simulated with the Monte Carlo method. This method has therefore found important applications, particularly in physics , and two books by the author Kurt Binder are among the most cited publications in this branch of science.
- The path of a single raindrop that collides with randomly distributed other drops can be simulated. After simulating several specific droplets, statements can be made about the average droplet size or about the temperature and droplet density at which snow or hail occurs.
- For the Galton board , the distribution of the balls on the compartments can be calculated using the binomial distribution, if the probability that a ball falls to the right is exactly 50% for the obstacles. If this is not the case, the overall experiment can be modeled in a Monte Carlo simulation. For this purpose, a suitable probability is assumed for each obstacle and a high number of ball throws is simulated according to these probabilities.
- If no analytical formula for the valuation of a financial product is known, Monte Carlo simulation can be used to find suitable distribution assumptions for the relevant random variables and to price complex financial contracts (such as “exotic” options) in a simple manner.
Examples
Miller-Rabin primality test
An example of a Monte Carlo simulation is the Miller-Rabin test , in which a probabilistic determination is made whether a natural number is prime or not. The output of the test is either "safely composed" or "probably prime". The probability that a composite number is classified as “probably prime” is less than 25% per run and can be further reduced by executing it multiple times. The Miller-Rabin test does not provide any information about the factors of a composite number, so it is not a factorization procedure .
Probabilistic determination of the number Pi
For this purpose, one selects random points and checks (by applying the Pythagorean theorem ) whether they lie within the unit circle :
- .
The ratio of the number of points inside and outside the circle can then be determined as follows:
Numerical integration

The above example for determining Pi practically forms the area integral of a quadrant. Correspondingly, the area integral of general, also higher-dimensional functions can be calculated using this method. Should be the integral
a function are calculated, then one selects independent points uniformly distributed in the interval and approximates through
In the more general case of higher-dimensional functions, the procedure is similar. Let be an arbitrary -dimensional set and an integrable function. About the value
To calculate approximately, one randomly chooses points for uniformly distributed in the set . Then approximated
the value as a function of arbitrarily precise. In order to calculate Pi as presented above, one has to choose and as the characteristic function of the unit circle. Here is the area of the unit circle.
In practice, Monte Carlo methods are mainly used for the calculation of high-dimensional integrals. Classic integration algorithms are strongly affected by the curse of dimensionality and can no longer be used. However, especially high-dimensional integrands are mostly strongly localized. In these cases, MCMC methods in particular allow the generation of samples with a distribution that allows such high-dimensional integrals to be calculated efficiently.
Supercomputers
Today's supercomputers ( HPC ) are based on massive multiprocessing with many thousands of individual processors working in parallel. These conditions can be exploited particularly well with such probabilistic solution methods. Supercomputers and MC methods are among others. a. used for the simulation of aging nuclear weapons (see also Stockpile stewardship ) of the USA.
Program packages
- MCNP , the Monte-Carlo N-Particle Transport Code , is a prototypical, worldwide widespread reactor physics program that is very often used, also in nuclear engineering and nuclear fusion engineering . The current version is MCNP6.2. On the MCNP website, manuals and release notes can be found as internet documents, for example Volume I of the MCNP manual Overview and Theory .
- PYTHIA is a simulation program for particle physics and simulates collisions and the resulting particles.
- SHERPA is a simulation program for high energy particle physics. Created at the TU Dresden , it is now being developed by an internationally distributed working group headed by Frank Krauss.
- SPICE is a simulation program for analog, digital and mixed electronic circuits. With the Monte Carlo simulation it is possible to calculate the effects of the scatter of the component values within the specified tolerance.
See also
literature
- Kurt Binder : Monte Carlo methods in statistical physics. Springer, Berlin [a. a.] 1979, ISBN 3-540-09018-5 .
- Kurt Binder: Applications of the Monte Carlo method in statistical physics. Springer, Berlin 1984, ISBN 3-540-12764-X .
- Paul Glasserman : Monte Carlo Methods in Financial Engineering. Springer, Berlin 2003, ISBN 978-1-4419-1822-2 .
- David P. Landau , Kurt Binder: A guide to Monte Carlo simulations in statistical physics. Cambridge University Press, Cambridge, 2014, ISBN 978-1107074026
Web links
- Interactive animation of the Monte Carlo simulation to estimate the number of circles π.
- The Monte Carlo simulation for particle physics. Film by the Karlsruhe Institute of Technology on the Monte Carlo simulation in particle physics on YouTube
Individual evidence
- ↑ Christophe Andrieu, Nando de Freitas, Arnaud Doucet, Michael I. Jordan: An Introduction to MCMC for Machine Learning (PDF, 1.0 MB), In: Machine Learning 2003 , Vol. 50, Vol. 1–2, p. 5 -43.
- ^ Lecture Notes in Structural Reliability - Engineering Risk Analysis Group; Technical University of Munich
- ^ N Metropolis: BEGINNING of the MONTE CARLO METHOD . Ed .: Los Alamos Science Special Issue. 1987, p. 125-130 ( fas.org [PDF]).
- ^ Douglas Hubbard, How to Measure Anything: Finding the Value of Intangibles in Business. John Wiley & Sons, 2007, p. 46.
- ^ Charles Grinstead, J. Laurie Snell: Introduction to Probability. American Mathematical Society, 1997, pp. 10-11.
- ^ HL Anderson: Metropolis, Monte Carlo and the MANIAC . (PDF, 829 kB) Los Alamos Science, No. 14, 1986, pp. 96-108, 1986.
- ↑ N. Metropolis, AW Rosenbluth, MN Rosenbluth, AH Teller, E. Teller: Equation of State Calculations by Fast Computing Machines. In: The Journal of Chemical Physics. Volume 21, Number 6, June 1953, pp. 1087-1092, doi : 10.1063 / 1.1699114 .
- ↑ M. Rosenbluth: Genesis of the Monte Carlo Algorithm for Statistical Mechanics , AIP Conference Proceedings, Volume 690, 2003, pp. 22–30, conference at LANL on the occasion of the 50th anniversary of the publication of the 1953 work
- ^ JE Gubernatis: "Marshall Rosenbluth and the Metropolis Algorithm , Physics of Plasmas, Volume 12, 2005, p. 057303.
- ↑ M. Rosenbluth, A. Rosenbluth: Further Results on Monte Carlo Equations of State , The Journal of Chemical Physics, Volume 22, 1954, pp. 881-884
- ↑ M. Rosenbluth, A. Rosenbluth: Monte Carlo Calculation of the Average Extension of Molecular Chains , The Journal of Chemical Physics, Volume 23, 1955, pp. 356-359
- ↑ Gleißner; W .: Risk analysis, risk quantification and risk aggregation, in: WiSt, 9/2017, pp. 4–11
- ↑ S. Jayraman: A Review of Monte Carlo Methods in Real Estate. May 2, 2013, accessed May 20, 2017 (English and sources therein).
- ↑ Klaus Bernhard Gablenz : Monte Carlo helps with uncertainties. In: Immobilienzeitung . Issue 29, July 26, 2007, p. 6 ( svgablenz.de [PDF]).
- ↑ David MacKay : Chapter 4.4 Typicality & Chapter 29.1 . In: Information Theory, Inference and Learning Algorithms . Cambridge University Press, 2003, ISBN 978-0-521-64298-9 .
- ↑ Prof. A. Bachem in Interview, c't 12/2010, p. 18: In this way, probabilistic solution methods can usually be parallelized far better than the deterministic methods that are common today.
- ↑ MERCURY. Retrieved August 13, 2019 .
- ↑ 2014 Jul 10: Trinity supercomputer to support nuclear stockpile simulations -. Accessed August 13, 2019 .
- ↑ Nicole Hemsoth: NNSA Stockpile of Nuclear Security supercomputer Continues Evolution. July 16, 2015. Retrieved August 13, 2019 (American English).
- ^ Stockpile Stewardship Program. Retrieved August 13, 2019 .
- ↑ The WorldCat bibliographic database lists more than 10,000 works that are dedicated to the MCNP program itself or to applications of the program
- ^ A General Monte Carlo N-Particle (MCNP) Transport Code: Monte Carlo Methods, Codes, & Applications Group. Retrieved June 19, 2018 .
- ↑ X-5 Monte Carlo Team: MCNP - A General Monte Carlo N-Particle Transport Code, Version 5: Volume I: Overview and Theory. Retrieved June 19, 2018 .









![\ left (x, y | x \ in \ left [-1..1 \ right] \ wedge y \ in \ left [-1..1 \ right] \ right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/323480dbfb59c62878e5144f29de6e71df8b3c0a)






![[0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)











![K: = [- 1,1] ^ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49cc626b4e8375a8346cd0f89a5e7974afa8f4bb)

