Buffon's needle problem

The Buffon needle problem asks for the probability that a randomly thrown needle intersects a grid of parallel lines. Among other things, it allows the number of circles to be determined experimentally. The problem belongs to the field of integral geometry and was one of the first in this field. Georges-Louis Leclerc de Buffon treated it for the first time in 1733 before the Paris Academy of Sciences and again in more detail in the supplement to his Histoire Naturelle 1777. ${\displaystyle \pi }$

Experimental implementation

Green dots describe an intersection of the sticks with the line.

As many identical chopsticks as possible are required. On a flat surface, parallel auxiliary lines are constructed at a distance . ${\displaystyle d}$

All existing chopsticks are randomly scattered on the surface. Finally you count how many sticks cross one of the lines.

If the distance between the lines is the same as the length of the sticks, an approximation for is obtained by multiplying the number of all sticks used by 2 and dividing by the number of sticks that cross a line. ${\displaystyle d}$ ${\displaystyle l}$ ${\displaystyle \pi }$

In the picture on the right, 11 of 17 double crochets cross a line; so it arises

${\displaystyle \pi \approx {\frac {2\cdot 17}{11}}\approx 3{,}1}$.

If (in the case of short sticks) the formula is ${\displaystyle d\geq l}$

${\displaystyle \pi \approx {\frac {2\cdot N_{A}\cdot l}{N_{C}\cdot d}}}$

to apply, where the number of all double crochets denotes the length . is the number of all bars that cross one of the lines and is the distance between two neighboring lines. ${\displaystyle N_{A}}$ ${\displaystyle l}$ ${\displaystyle N_{C}}$ ${\displaystyle d}$

The formula for the hit probability (derived in the following section) was used. According to the law of large numbers , the relative frequency in practical implementation for a large number of rods approaches the given probability: and thus for . ${\displaystyle p={\tfrac {2\cdot l}{\pi \cdot d}}}$ ${\displaystyle {\tfrac {N_{C}}{N_{A}}}\rightarrow p}$ ${\displaystyle {\tfrac {2\cdot N_{A}\cdot l}{N_{C}\cdot d}}\rightarrow \pi }$ ${\displaystyle N_{A}\rightarrow \infty }$

In the case (the case of long rods) the relationship is a little more complicated. ${\displaystyle d<l}$

Proof for needles of any length

The angle ${\displaystyle \varphi }$

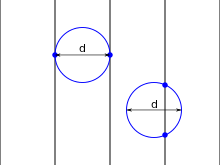
For the case (short needle) just consider a horizontal strip of width d, see figure on the right for the case . A needle of the length touches the edge if the end point of the needle lying on the vertical dashed line lies within a strip the width of one of the two edges. The likelihood of this is . Integration over gives the probability that the needle will touch a line: ${\displaystyle l\leq d}$ ${\displaystyle l=d}$ ${\displaystyle l}$ ${\displaystyle l|{\cos {\varphi }}|}$ ${\displaystyle {\tfrac {l|{\cos {\varphi }}|}{d}}}$ ${\displaystyle {\varphi }}$

${\displaystyle p=\int _{0}^{2\pi }{\frac {l|{\cos {\varphi }}|}{d}}{\frac {d\varphi }{2\pi }}={\frac {2l}{\pi d}}}$

In the case (long needle) one has to take into account the possibility of multiple touching of lines, so that the formulas become more complicated: ${\displaystyle l>d}$

${\displaystyle p={\frac {2}{\pi }}\left({\frac {l}{d}}-{\sqrt {\left({\frac {l}{d}}\right)^{2}-1}}+\operatorname {arcsec} {\frac {l}{d}}\right)}$

You can also use the arc secan in the last formula instead of the arc secan . In the case , both formulas result . In the case of the long needle, it grows strictly monotonously with the length of the needle and goes for towards 1. ${\displaystyle \operatorname {arcsec} {x}=\arccos {\tfrac {1}{x}}={\tfrac {\pi }{2}}-\arcsin {\tfrac {1}{x}}}$ ${\displaystyle d=l}$ ${\displaystyle p={\tfrac {2}{\pi }}}$ ${\displaystyle p}$ ${\displaystyle l}$ ${\displaystyle l\to \infty }$

Barber's Proof of Small Needles

For Barbier's proof: Two points of intersection or contact for circles of diameter d

In 1860 Barbier gave a proof for the case of small needles that does not require integration. First of all, it is shown that the expected value for the number of hits is a linear function of the length of the needle ( with the length ), which also applies to any curves, since they can be approximated by a path. The constant of proportionality c is to be determined. For this purpose, the case of circles with diameter d is considered, which always have exactly 2 hits on the parallel lines at a distance d. The circle is approximated by inscribed and circumscribed polygons P, Q (with the circumference p or q) and we get: ${\displaystyle E}$ ${\displaystyle E=cl}$ ${\displaystyle l}$

${\displaystyle E(P)=cp\leq 2\leq E(Q)=cq}$

And when the number of sides of the polygons reaches the limit:

${\displaystyle cd\pi \leq 2\leq cd\pi }$

so and thus the desired result . ${\displaystyle c={\tfrac {2}{d\pi }}}$ ${\displaystyle E={\tfrac {2l}{d\pi }}}$

Because of its elegance, the proof of Barbier von Aigner and Ziegler was included in The Book of Proofs .

Generalizations

You can ask about figures other than lines that are randomly thrown onto a plane, for example polygons. From the formula for the Buffon problem it follows for polygons with a diameter smaller and the circumference the hit probability ${\displaystyle d}$ ${\displaystyle U}$

${\displaystyle p={\frac {2U}{\pi d}}}$.

If a closed curve is approximated by such a polygon, the probability of a hit also results in this case if the circumference of the polygon is replaced by the length of the curve (here too, the diameter must be smaller ). These are the starting points for methods of integral geometry to obtain formulas, for example for the arc length of curves, from suitable hit probabilities. ${\displaystyle U}$ ${\displaystyle d}$

In the so-called Buffon-Laplace needle problem one asks about the hit probability for a rectangular grid with side lengths and . For small needles ( and ) results ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle l<a}$ ${\displaystyle l<b}$

${\displaystyle p={\frac {2l(a+b)-l^{2}}{\pi ab}}}$.

The problem can also be extended to the throwing of other bodies, as in the Franc-Carreau problem, also addressed by Buffon in 1733 : you throw a coin (circular disc, diameter ) on a square grid (side length ), where is. What is the probability that the coin will come to rest on the edge? Since the coin can only touch the edge if its center is at a distance from the edge, the hit probability can be specified as an area ratio through simple geometric considerations: ${\displaystyle l}$ ${\displaystyle d}$ ${\displaystyle l<d}$ ${\displaystyle {\tfrac {l}{2}}}$

${\displaystyle p={\frac {d^{2}-{(d-l)}^{2}}{d^{2}}}={\frac {l}{d}}\left(2-{\frac {l}{d}}\right)}$

For a fair game it must be. ${\displaystyle l=d(1-{\tfrac {1}{\sqrt {2}}})\approx 0{,}293\cdot d}$

Historical

Buffon reported the needle problem and similar problems to the French Academy of Sciences in 1733, as reported by Fontenelle . It was of interest in connection with a game popular with nobles at the time: you throw a coin at a tile pattern and bet on the position of the coin whether it touches one of the cracks or not ( Franc-Carreau problem ). Buffon went into this in more detail in 1777, assuming the correct answer in the case of the needle problem. In particular, he derived from the formula for short needles that for fair betting (i.e., for bets with a 50 percent chance of winning), the needle problem must be the ratio . For the throw on a square grid, however, he gave a wrong formula. The correct formula (also in the case of a rectangular grid) was only given by Pierre Simon de Laplace in 1812, without mentioning Buffon. He cited this as an example of the application of probability theory to the determination of curve lengths and areas. This was then carried out by Isaac Todhunter among others in 1865. Working with Buffon's needle problem also resulted in Crofton's formula (see Morgan Crofton ) for the arc length of a curve in integral geometry (1868). ${\displaystyle {\tfrac {l}{d}}={\tfrac {\pi }{4}}}$

A certain Mario Lazzarini is said to have carried out the most extensive experimental test of the formula in 1901 (with a specially built machine), with 3408 throws of needles with an aspect ratio . His result was 1,808 hits, then a value of that of revealed to six decimal places exactly. However, the numbers he provided are suspicious (other authors interpreted this as a stroke of luck) and appear to be tailored to the known approximation for . The astronomer Wolf carried out the experiment in 1850 and received 2532 hits with 5000 throws, according to an estimate for von Further experiments Ambrose Smith carried out in 1855 with 3204 throws ( ) with 1218 hits, which results in a value of . Hans-J. Bentz performed the experiment with 2000 litters and received for . ${\displaystyle {\tfrac {l}{d}}={\tfrac {5}{6}}}$ ${\displaystyle \pi }$ ${\displaystyle 3{,}1415929\ldots }$ ${\displaystyle {\tfrac {355}{113}}}$ ${\displaystyle \pi }$ ${\displaystyle {\tfrac {l}{d}}=0{,}8}$ ${\displaystyle \pi }$ ${\displaystyle 3{,}1596}$ ${\displaystyle {\tfrac {l}{d}}=0{,}6}$ ${\displaystyle \pi }$ ${\displaystyle 3{,}155\ldots }$ ${\displaystyle 3{,}1430\ldots }$ ${\displaystyle \pi }$

literature

• Martin Aigner , Günter M. Ziegler : The book of proofs , Springer Verlag 2002, chapter 24 The needle problem by Buffon , pp. 179-182
• Maurice George Kendall , PAP Moran: Geometric Probability , London: Charles Griffin, 1963, pp. 70ff
• P. Holgate: Buffon's cycloid , Studies in the history of probability and statistics XXXIX, Biometrika 68 (3) (1981), 712-716 (for history)
• Magdalena Hyksova, Anna Kalousova, Ivan Saxl: Early history of geometric probability and stereology , Image Anal. Stereology 31, 2012, 1-16, pdf
• Isaac Todhunter : A History of the mathematical theory of probability from the time of Pascal to that of Laplace , Macmillan 1865, pp. 347ff, Archive
• Persi Diaconis : Buffon's Needle Problem with a Long Needle , J. Appl. Prob. 13, 1976, pp. 614–618 (distribution of the number of hits with long needles)
• L. Schroeder: Buffon's needle problem: An exciting application of many mathematical concepts , Mathematics Teacher, 67, 1974, pp. 183-186
• James Victor Uspensky : Introduction to Mathematical Probability , McGraw Hill 1937, p. 112ff

Web links

• Eric Weisstein: Buffon's Needle Problem . In: MathWorld (English).
• Paul Kunkel Buffon's Needle
• Buffon's Needle Problem, Cut the Knot, Alex Bogomolny
• Buffon's Needle Problem, Cut the Knot, Scott Brodie

Individual evidence

1. ↑ Later it turned out that Isaac Newton had also made considerations in this area, but did not publish them
2. ^ Isaac Todhunter: History of the Mathematical Theory of Probability , 1865, p. 203
3. ^ John J. O'Connor, Edmund F. Robertson :  Georges Louis Leclerc Comte de Buffon. In: MacTutor History of Mathematics archive .
4. ↑ Buffon: Essai d'arithmétique morale , Histoire naturelle, générale er particulière, Supplément 4, 46-123, 1777. The essay is from around 1760. Todhunter, History of the Mathematical Theory of Probability , 1865, p. 344
5. ↑ Eric Weisstein: Buffon's Needle Problem . In: MathWorld (English).
6. ↑ The derivation is not much more difficult. In the area of ​​integration, a distinction is made between an area in which only one contact can take place, in which integration can be carried out as with short needles, and an area with at least one contact, where the probability is 1. See Aigner, Ziegler.
7. ^ E. Barbier: Note on the problem of l'aiguelle et le jeu du joint couvert , J. Math. Pures et Appliqués, Volume 5, 1860, pp. 273-286
8. ↑ Aigner, Ziegler: The Book of Proofs , Springer Verlag, Chapter 24
9. ↑ For example Boris Wladimirowitsch Gnedenko Theory of Probability , MIR Publishers, 1978, p. 38f
10. ↑ Eric Weisstein: Buffon-Laplace Needle Problem . In: MathWorld (English).
11. ↑ Diderot, Encyclopedia 1752 on the Franc Carreau Problem, PDF
12. ^ Histoire de l'Academie royale des Sciences, année 1733, Paris 1735, pp. 43–45, only in a short communication
13. ^ Laplace: Théorie analytique des probabilités , Paris: Veuve Courcier, 1812, pp. 359ff
14. ↑ For more details on the analysis of results like that of Lazzarini: Gnedenko Theory of Probability , MIR 1978, p. 37f. If the number of throws is less than 5000, it follows from elementary considerations that if the number of hits is changed by 1, the fourth decimal place is changed. According to Gnedenko, the probability of obtaining precisely this numerical value in the case of Lazzarini's experiment is less than three percent. ${\displaystyle \pi }$
15. ↑ Kendall, Moran: Geometric Probability , p. 70 jokingly make the following entry by NT Gridgeman in their table of experiments ( Geometric Probability and the Number Pi , Scripta Mathematica 25, 1960, 183-195): Number of throws: 2, Hit: 1 ,, gives the approximation for of ${\displaystyle {\tfrac {l}{d}}=0{,}7857}$ ${\displaystyle \pi }$ ${\displaystyle 3{,}143}$
16. ↑ According to Aigner, Ziegler: ${\displaystyle 3408\cdot {\tfrac {5}{6}}=2840=8\cdot 355}$
17. ↑ See also: Lee Badger: Lazzarini's Lucky Approximation of π , Mathematics Magazine, Volume 67, 1994, 83-91
18. ^ Biography of Wolf in the ADB by Siegmund Günther
19. ^ Kendall, Moran: Geometric Probability , p. 70
20. ↑ Augustus De Morgan reports on this in A Budget of Paradoxes 1872, see Uspensky: Introduction to Mathematical Probability , 113
21. ↑ To be precise, 1213 in 11 unclear cases, half of which were assessed
22. ↑ H.-J. Bentz: Das Buffon-Nadelproblem (1777) , Praxis der Mathematik, 22, 1980, Heft 6, S. 167-171
23. ↑ Simulation with a computer program ( Monte Carlo method ): Hans-J. Bentz: For the simulation of the Buffon needle problem , Praxis der Mathematik, 24, 1982, issue 5, pp. 129-137