Galton board

Model of a galton board

Play media file

Video Galton board

Galton board with falling balls

A Galton board (after Francis Galton ), also called a random board or Galton's nail board , is a mechanical model for demonstrating and visualizing the binomial distribution , a probability distribution that plays a role in many random experiments .

concept

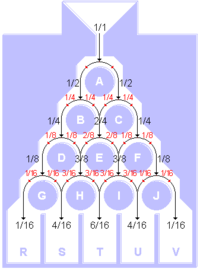
The Galton board consists of a regular arrangement of obstacles against which a ball thrown in from above can bounce off to the left or right. After passing the obstacles, the balls are caught in compartments to be counted there.

The Galton board simulates a physical measuring device whose measured value is noisy. The horizontal position of the sphere is the value to be measured, which is still exactly present at the upper input, while it was changed in one of the compartments by a noise signal below. The obstacles symbolize small disturbances that can influence the measured value positively or negatively. In total, they can grow into a larger disruption, but they can also add up to zero. At the end of the day, the filling levels of the compartments provide information about the frequency distribution of the various strengths of the accumulated disturbances. In real measurements, for example, this corresponds to the noise distribution of an electrical signal, caused by a large number of very small interference signals, which can contribute just as positively as negatively. A fundamental mathematical law, the central limit theorem , guarantees that an almost arbitrarily composed distribution of such very small and very numerous individual perturbations converges in the sum against the bell-shaped Gaussian normal distribution. If the requirements for such a noise distribution are met, one speaks of Gaussian noise. With a finite number of perturbations, as in the Galton board, the binomial distribution is obtained , which in the limit of many perturbations and many compartments also converges to the normal distribution, see Moivre-Laplace's limit theorem . The statistical regularities of such a random measurement noise can be studied and checked clearly using the Galton board.

Mathematical consideration

Each time a ball hits one of the obstacles, it is a Bernoulli attempt . The two possible outcomes are “ball falls to the right” (X = 1) and “ball falls to the left” (X = 0).

If the structure is symmetrical , the probability of falling to the right and the probability of falling to the left are . By an asymmetrical structure or by tilting the board you can also achieve a different value for , but of course still is, because the balls that do not fall to the right fall to the left. This case is discussed below. ${\ displaystyle P (X = 1) = p = 1/2}$ ${\ displaystyle P (X = 0) = q = 1/2}$ ${\ displaystyle p}$ ${\ displaystyle q = 1-p}$

As the ball hits a new one after passing the first obstacle, for which the same conditions apply, another Bernoulli attempt is carried out here; running through the entire device is therefore a multi-level Bernoulli chain, with the number of horizontal rows of obstacles being the length of this chain. The picture shown is therefore a repetition of a Bernoulli experiment four times, i.e. H. a Bernoulli chain of length 4.

You can now calculate the probability of a ball falling into a certain compartment. If there is only one obstacle (A), the probability is 1/2 for the left and for the right, or to put it another way, on average half of all balls fall to the right and half to the left. This means that half of the balls hit B and the other half hit C, where they split again with equal probabilities to the left and right. But this means that only 1/4 of the balls at B fall to the left, 1/4 at C to the right, and 1/4 from the left and from the right into the space between B and C. Here the probabilities add up, and 1 / 4 + 1/4 = 2/4 (= 1/2, but not shortened on purpose ) falls through the middle between B and C.

With the help of the figure, you can follow how the flow of balls is divided at each row of obstacles (for the next row you will therefore have to count eighths, for the next but one with sixteenths of the total) and, on the other hand, reunite in every space between two adjacent obstacles .

The resulting probabilities after the last division and combination at the lowest row of obstacles (G, H, I, J) are the probabilities with which the balls will fall into the compartments (R, S, T, U, V).

In the example, all of these probabilities have the denominator 16, since there are 4 rows of obstacles (16 = 2 ⁴ ). The counters are obtained by adding the counters in the series above, which corresponds to the union of the ball streams in the spaces in between. This results in the following scheme for the probabilities:

                  Zähler:        Nenner:
    Reihe 0:         1           1 → =2^0
          1:        1,1          2 → =2^1
          2:       1,2,1         4 → =2^2
          3:      1,3,3,1        8 → =2^3
          4:     1,4,6,4,1      16 → =2^4

It can be seen that the counters are the binomial coefficients because they are created according to the Pascal triangle scheme . The denominators are powers of 2, they follow from the probability of falling to the right or left. ${\ displaystyle p = q = 1/2}$

The compartments R, S, T, U, V can be numbered according to how often a ball has to fall to the right to reach the respective compartment. This gives compartment R the number 0, because a ball that lands in R has never fallen to the right, but only to the left. Compartment S has the number 1, because a ball that lands here has fallen to the right exactly once (in the first, second, third or fourth row, but only this once). The other subjects are given the numbers 2, 3, and 4 accordingly.

The result is similar to a binomial distribution. Since the cavities between the obstacles are too large compared to the balls, some balls are not deflected. This falsifies the result and the middle bar appears too high.

The probability of falling into the 0 bin is

{\ displaystyle B (0) = 1 \ cdot \ left ({\ frac {1} {2}} \ right) ^ {4} = {\ frac {1} {16}}.}

The probability of falling into compartment 1 is

{\ displaystyle B (1) = 4 \ cdot \ left ({\ frac {1} {2}} \ right) ^ {4} = {\ frac {4} {16}}.}

It also follows:

{\ displaystyle B (2) = 6 \ cdot \ left ({\ frac {1} {2}} \ right) ^ {4} = {\ frac {6} {16}},}

{\ displaystyle B (3) = 4 \ cdot \ left ({\ frac {1} {2}} \ right) ^ {4} = {\ frac {4} {16}},}

{\ displaystyle B (4) = 1 \ cdot \ left ({\ frac {1} {2}} \ right) ^ {4} = {\ frac {1} {16}}.}

In general, the following applies to the subject : ${\ displaystyle k}$

{\ displaystyle B (k) = {4 \ choose k} \ cdot \ left ({\ frac {1} {2}} \ right) ^ {4} = {4 \ choose k} \ cdot {\ frac {1 } {16}}.}

Here is the binomial coefficient in row 4, column of Pascal's triangle (Note: the columns are the numbers of the compartments, so they start with 0). ${\ displaystyle {4 \ choose k}}$ ${\ displaystyle k}$

If the formula is generalized further to a Galton board with rows of obstacles (instead of 4, as in the example), i.e. to a Bernoulli chain of length , the following applies: ${\ displaystyle n}$ ${\ displaystyle n}$

{\ displaystyle B (k, n) = {n \ choose k} \ cdot \ left ({\ frac {1} {2}} \ right) ^ {n} = {n \ choose k} \ cdot {\ frac {1} {2 ^ {n}}}}

.

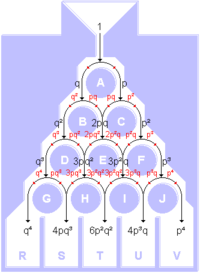
For further generalization, imagine an asymmetrical Galton board, where the probabilities for left and right are not the same. The balls fall with the probability to the right and to the left. ${\ displaystyle p}$ ${\ displaystyle q = 1-p}$

Then they end up in compartment 0 with the probability q ⁴ instead of (1/2) ⁴ , because they still have to fall four times to the left, but now each do so with the probability . ${\ displaystyle q}$

In the rightmost compartment (for which you have to fall to the right four times, which you do with the probability of doing this) you land with . ${\ displaystyle p}$ ${\ displaystyle p ^ {4}}$

Result when the Galton board is tilted, here the probability p is approx. 0.9.

For the other compartments they have to fall to the right according to the number ( ) and to the left the other times ( ). They do this with the probabilities respectively . What does not change are the unions of the spherical streams in the spaces in between. The binomial coefficients remain unaffected. The general formula for a 4-row Galton board with the probability of falling to the right is therefore: ${\ displaystyle k}$ ${\ displaystyle k}$ ${\ displaystyle 4-k}$ ${\ displaystyle p ^ {k}}$ ${\ displaystyle q ^ {4-k} = (1-p) ^ {4-k}}$ ${\ displaystyle p}$

{\ displaystyle B (k, p, 4) = {4 \ choose k} \ cdot p ^ {k} \ cdot q ^ {4-k} = {4 \ choose k} \ cdot p ^ {k} \ cdot (1-p) ^ {4-k}.}

And for the general formula of a correspondingly- row board follows: ${\ displaystyle n}$

{\ displaystyle B (k, p, n) = {n \ choose k} \ cdot p ^ {k} \ cdot q ^ {nk} = {n \ choose k} \ cdot p ^ {k} \ cdot (1 -p) ^ {nk}.}

This is then exactly the binomial distribution of a Bernoulli chain of length with and . ${\ displaystyle n}$ ${\ displaystyle P (1) = p}$ ${\ displaystyle P (0) = q = 1-p}$

Web links

Commons : Galtonbrett - collection of images, videos and audio files

Java applet for illustration
Galton board - physical simulation in HTML5
Galton board variable - flexible simulation including tasks

literature

Gerd Binnig : Out of nowhere. About the creativity of nature and people. 2nd Edition. Piper, Munich et al. 1997, ISBN 3-492-21486-X .
Sir Francis Galton : Natural inheritance. Macmillan, London 1889 (contains the description of the Galton board).