Binomial distribution

Binomial distribution
Probability distribution
Distribution function
parameter	${\displaystyle n\in \mathbb {N} ^{+}}$, ${\displaystyle p\in [0,1]}$
carrier	${\displaystyle k\in \{0,\dotsc ,n\}}$
Probability function	${\displaystyle \textstyle {n \choose k}\,p^{k}(1-p)^{n-k}}$
Distribution function	${\displaystyle I_{1-p}(n-\lfloor k\rfloor ,1+\lfloor k\rfloor )}$
Expected value	${\displaystyle np}$
Median	i. A. no closed formula, see below
mode	${\displaystyle \lfloor (n+1)p\rfloor }$ or ${\displaystyle \lfloor (n+1)p-1\rfloor }$
Variance	${\displaystyle np(1-p)}$
Crookedness	${\displaystyle {\frac {1-2p}{\sqrt {np(1-p)}}}}$
Bulge	${\displaystyle 3+{\frac {1-6p(1-p)}{np(1-p)}}}$
entropy	${\displaystyle {\frac {1}{2}}\log _{2}{\big (}2\pi \mathrm {e} \,np(1-p){\big )}}$ ${\displaystyle +{\mathcal {O}}\left({\frac {1}{n}}\right)}$
Moment generating function	${\displaystyle \left(1-p+p\mathrm {e} ^{t}\right)^{n}}$
Characteristic function	${\displaystyle \left(1-p+p\mathrm {e} ^{\mathrm {i} t}\right)^{n}}$

Probability function of the binomial distribution for ; (blue), (green) and (red) ${\displaystyle n=20}$ ${\displaystyle p=0{,}1}$ ${\displaystyle p=0{,}5}$ ${\displaystyle p=0{,}8}$

Binomial distributions for with and as in Pascal's triangle The probability that a ball in a Galton board with eight levels ( ) will fall into the middle compartment ( ) is . ${\displaystyle p=0{,}5}$
${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle n=8}$ ${\displaystyle k=4}$ ${\displaystyle 70/256}$

The binomial distribution is one of the most important discrete probability distributions .

It describes the number of successes in a series of similar and independent experiments, each of which has exactly two possible results (“success” or “failure”). Such series of experiments are also called Bernoulli processes .

If the probability of success in one attempt and the number of attempts, then one designates with (also , or ) the probability of achieving exactly successes (see section definition ). ${\displaystyle p}$ ${\displaystyle n}$ ${\displaystyle B(k\mid p,n)}$ ${\displaystyle B_{n,p}(k)}$ ${\displaystyle B(n,p,k)}$ ${\displaystyle B(n;p;k)}$ ${\displaystyle k}$

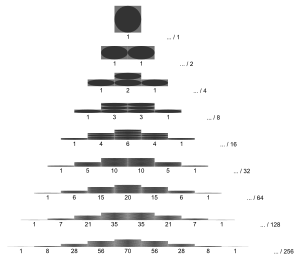
The binomial distribution and Bernoulli's experiment can be illustrated with the help of the Galton board . It is a mechanical device into which bullets are thrown. These then fall randomly into one of several subjects, with the division corresponding to the binomial distribution. Depending on the construction, different parameters and are possible. ${\displaystyle n}$ ${\displaystyle p}$

Although the binomial distribution was known long before, the term was first used in 1911 in a book by George Udny Yule .

Examples

The probability of rolling a number greater than 2 with a normal dice is ; the probability that this will not be the case is . Assuming you roll the dice 10 times ( ), there is a small probability that a number greater than 2 will not be rolled once, or vice versa every time. The probability of throwing such a number times is described by the binomial distribution . ${\displaystyle p={\tfrac {4}{6}}={\tfrac {2}{3}}}$ ${\displaystyle q}$ ${\displaystyle q=1-p={\tfrac {1}{3}}}$ ${\displaystyle n=10}$ ${\displaystyle k}$ ${\displaystyle (0\leq k\leq 10)}$ ${\displaystyle B_{n,p}(k)}$

The process described by the binomial distribution is often illustrated by a so-called urn model . In an urn z. B. 6 balls, 2 of them black, the others white. Reach into the urn 10 times, take out a ball, note its color and put the ball back. In a special interpretation of this process, the drawing of a white ball is understood as a "positive event" with the probability , the drawing of a non-white ball as a "negative result". The probabilities are distributed in the same way as in the previous example of rolling the dice. ${\displaystyle p}$

definition

Probability function, (cumulative) distribution function, properties

The discrete probability distribution with the probability function

${\displaystyle B(k\mid p,n)={\begin{cases}{\binom {n}{k}}p^{k}(1-p)^{n-k}&{\text{falls}}\quad k\in \left\{0,1,\dots ,n\right\}\\0&{\text{sonst.}}\end{cases}}}$

is called the binomial distribution for the parameters (number of attempts) and (the success or hit probability ). ${\displaystyle n}$ ${\displaystyle p\in \left[0,1\right]}$

The above formula can be understood as follows: We need exactly successes of the probability for all experiments and consequently we have exactly failures of the probability . However, any of the successes can occur in any of the attempts, so we still have to multiply by the number of -element subsets of an -element set. Because there are just as many possibilities to choose the successful ones from all attempts . ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle p^{k}}$ ${\displaystyle n-k}$ ${\displaystyle (1-p)^{n-k}}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle {\tbinom {n}{k}}}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle k}$

The probability of failure complementary to the probability of success is often abbreviated with . ${\displaystyle p}$ ${\displaystyle 1-p}$ ${\displaystyle q}$

As is necessary for a probability distribution, the probabilities for all possible values must add up to 1. This results from the binomial theorem as follows: ${\displaystyle k}$

${\displaystyle \sum _{k=0}^{n}{\binom {n}{k}}p^{k}(1-p)^{n-k}=\left(p+\left(1-p\right)\right)^{n}=1^{n}=1}$

A randomly distributed variable is accordingly called binomially distributed with the parameters and as well as the distribution function ${\displaystyle B(\cdot \mid p,n)}$ ${\displaystyle X}$ ${\displaystyle n}$ ${\displaystyle p}$

${\displaystyle F_{X}(x)=\operatorname {P} (X\leq x)=\sum _{k=0}^{\lfloor x\rfloor }{\binom {n}{k}}p^{k}(1-p)^{n-k}}$,

where denotes the rounding function. ${\displaystyle \lfloor x\rfloor }$

Other common notations of the cumulative binomial distribution are , and . ${\displaystyle F(k\mid p,n)}$ ${\displaystyle F(n,p,k)}$ ${\displaystyle F(n;p;k)}$

Derivation as Laplace probability

Scheme of experiment: An urn contains balls, of which are black and white. So the probability of drawing a black ball is . Balls are taken one after the other at random , their color is determined and then put back again. ${\displaystyle N}$ ${\displaystyle M}$ ${\displaystyle N-M}$ ${\displaystyle p}$ ${\displaystyle p={\frac {M}{N}}}$ ${\displaystyle n}$

We calculate the number of possibilities in which black balls can be found, and from this the so-called Laplace probability (“number of possibilities favorable for the event, divided by the total number of (equally probable) possibilities”). ${\displaystyle k}$

There are options for each of the draws, so overall options for selecting the balls. In order for these balls to be black, the draws must have a black ball. There are possibilities for every black ball, and possibilities for every white ball . The black balls can still be distributed across the draws in possible ways , so there is ${\displaystyle n}$ ${\displaystyle N}$ ${\displaystyle N^{n}}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle M}$ ${\displaystyle N-M}$ ${\displaystyle k}$ ${\displaystyle {\tbinom {n}{k}}}$ ${\displaystyle n}$

${\displaystyle {\binom {n}{k}}M^{k}(N-M)^{n-k}}$

Cases where exactly black balls have been selected. So the probability of finding exactly black balls among balls is: ${\displaystyle k}$ ${\displaystyle p_{k}}$ ${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle {\begin{aligned}p_{k}&={\binom {n}{k}}{\frac {M^{k}(N-M)^{n-k}}{N^{n}}}\\&={\binom {n}{k}}\left({\frac {M}{N}}\right)^{k}\left({\frac {N-M}{N}}\right)^{n-k}\\&={\binom {n}{k}}p^{k}(1-p)^{n-k}\end{aligned}}}$

properties

symmetry

• The binomial distribution is in the special cases , and symmetrical and otherwise asymmetrical. ${\displaystyle p=0}$ ${\displaystyle p=0{,}5}$ ${\displaystyle p=1}$
• The binomial distribution has the property ${\displaystyle B(k|p,n)=B(n-k|1-p,n).}$

Expected value

The binomial distribution has the expected value . ${\displaystyle np}$

proof

The expected value is calculated directly from the definition and the binomial theorem to ${\displaystyle \mu }$ ${\displaystyle \mu =\sum _{i=1}^{n}x_{i}p_{i}}$

${\displaystyle {\begin{aligned}\mu &=\sum _{k=0}^{n}k{\binom {n}{k}}p^{k}(1-p)^{n-k}\\&=np\sum _{k=0}^{n}k{\frac {(n-1)!}{(n-k)!k!}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{k=1}^{n}{\frac {(n-1)!}{(n-k)!(k-1)!}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{k=1}^{n}{\binom {n-1}{k-1}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{\ell =0}^{n-1}{\binom {n-1}{\ell }}p^{\ell }(1-p)^{(n-1)-\ell }\quad {\text{mit }}\ell :=k-1\\&=np\sum _{\ell =0}^{m}{\binom {m}{\ell }}p^{\ell }(1-p)^{m-\ell }\qquad {\text{mit }}m:=n-1\\&=np\left(p+\left(1-p\right)\right)^{m}=np1^{m}=np.\end{aligned}}}$

Alternatively, you can use that -distributed random variable as a sum of independent Bernoulli distributed random variables with can be written. With the linearity of the expected value it then follows ${\displaystyle B(\cdot \mid p,n)}$ ${\displaystyle X}$ ${\displaystyle n}$ ${\displaystyle X_{i}}$ ${\displaystyle \operatorname {E} (X_{i})=p}$

${\displaystyle \operatorname {E} (X)=\operatorname {E} (X_{1}+\dotsb +X_{n})=\operatorname {E} (X_{1})+\dotsb +\operatorname {E} (X_{n})=np.}$

Alternatively, the following proof can also be given with the help of the binomial theorem: Differentiate in the equation

${\displaystyle (a+b)^{n}=\sum _{k=0}^{n}{\tbinom {n}{k}}a^{k}b^{n-k}}$

both sides after , arises ${\displaystyle a}$

${\displaystyle n(a+b)^{n-1}=\sum _{k=0}^{n}k{\tbinom {n}{k}}a^{k-1}b^{n-k}}$,

so

${\displaystyle na(a+b)^{n-1}=\sum _{k=0}^{n}k{\tbinom {n}{k}}a^{k}b^{n-k}}$.

The desired result follows with and . ${\displaystyle a=p}$ ${\displaystyle b=1-p}$

Variance

The binomial distribution has the variance with . ${\displaystyle npq}$ ${\displaystyle q=1-p}$

proof

Let it be a -distributed random variable. The variance is determined directly from the shift set to ${\displaystyle X}$ ${\displaystyle B(n,p)}$ ${\displaystyle \operatorname {Var} (X)=\operatorname {E} \left(X^{2}\right)-\left(\operatorname {E} \left(X\right)\right)^{2}}$

${\displaystyle \operatorname {Var} (X)=\sum _{k=0}^{n}k^{2}\cdot P(X=k)-(np)^{2}}$

${\displaystyle =\sum _{k=0}^{n}k^{2}\cdot {n \choose k}p^{k}(1-p)^{n-k}-n^{2}p^{2}}$

${\displaystyle ={\cancel {n^{2}p^{2}}}-np^{2}+np{\cancel {-n^{2}p^{2}}}}$

${\displaystyle =np(1-p)=npq}$

or alternatively, from the equation of Bienaymé applied to the variance of independent random variables when considering that the identical individual processes of the Bernoulli distribution with enough to ${\displaystyle X_{i}}$ ${\displaystyle \operatorname {Var} (X_{i})=p(1-p)=pq}$

${\displaystyle \operatorname {Var} (X)=\operatorname {Var} (X_{1}+\dotsb +X_{n})=\operatorname {Var} (X_{1})+\dotsb +\operatorname {Var} (X_{n})=n\operatorname {Var} (X_{1})=np\left(1-p\right)=npq.}$

The second equality holds because the individual experiments are independent, so that the individual variables are uncorrelated.

Coefficient of variation

The coefficient of variation is obtained from the expected value and the variance

${\displaystyle \operatorname {VarK} (X)={\sqrt {\frac {1-p}{np}}}.}$

Crookedness

The skew arises too

${\displaystyle \operatorname {v} (X)={\frac {1-2p}{\sqrt {np(1-p)}}}.}$

Bulge

The curvature can also be shown closed as

${\displaystyle \beta _{2}=3+{\frac {1-6pq}{npq}}.}$

That’s the excess

${\displaystyle \gamma ={\frac {1-6pq}{npq}}.}$

mode

The mode , i.e. the value with the maximum probability, is for equal and for equal . If is a natural number, is also a mode. If the expected value is a natural number, the expected value is equal to the mode. ${\displaystyle p<1}$ ${\displaystyle k=\lfloor np+p\rfloor }$ ${\displaystyle p=1}$ ${\displaystyle n}$ ${\displaystyle np+p}$ ${\displaystyle k=np+p-1}$

proof

Be without limitation . We consider the quotient ${\displaystyle 0<p<1}$

${\displaystyle \alpha _{k}:={\frac {B(k+1\mid p,n)}{B(k\mid p,n)}}={\frac {\,{\frac {n!}{(k+1)!(n-k-1)!}}\,}{\frac {n!}{k!(n-k)!}}}\cdot {\frac {p^{k+1}(1-p)^{n-k-1}}{p^{k}(1-p)^{n-k}}}={\frac {n-k}{k+1}}\cdot {\frac {p}{1-p}}}$.

Now , if and if . So: ${\displaystyle \alpha _{k}>1}$ ${\displaystyle k<np+p-1}$ ${\displaystyle \alpha _{k}<1}$ ${\displaystyle k>np+p-1}$

${\displaystyle {\begin{aligned}k>(n+1)p-1\Rightarrow \alpha _{k}<1\Rightarrow B(k+1\mid p,n)<B(k\mid p,n)\\k=(n+1)p-1\Rightarrow \alpha _{k}=1\Rightarrow B(k+1\mid p,n)=B(k\mid p,n)\\k<(n+1)p-1\Rightarrow \alpha _{k}>1\Rightarrow B(k+1\mid p,n)>B(k\mid p,n)\end{aligned}}}$

And only in this case does the quotient have the value 1, i.e. H. . ${\displaystyle np+p-1\in \mathbb {N} }$ ${\displaystyle B(np+p-1\mid n,p)=B(np+p\mid n,p)}$

Median

It is not possible to give a general formula for the median of the binomial distribution. Therefore, different cases have to be considered that provide a suitable median:

• If a natural number, then the expected value, median and mode match and are the same . ${\displaystyle np}$ ${\displaystyle np}$
• A median lies in the interval . Here denote the rounding function and the rounding function . ${\displaystyle m}$ ${\displaystyle \lfloor np\rfloor \leq m\leq \lceil np\rceil }$ ${\displaystyle \lfloor \cdot \rfloor }$ ${\displaystyle \lceil \cdot \rceil }$
• A median can not deviate too much from the expected value: . ${\displaystyle m}$ ${\displaystyle |m-np|\leq \min\{\ln 2,\max\{p,1-p\}\}}$
• The median is unique and matches round if either or or (unless and is even). ${\displaystyle m=}$ ${\displaystyle (np)}$ ${\displaystyle p\leq 1-\ln 2}$ ${\displaystyle p\geq \ln 2}$ ${\displaystyle |m-np|\leq \min\{p,1-p\}}$ ${\displaystyle p=1/2}$ ${\displaystyle n}$
• If and is odd, then every number in the interval is a median of the binomial distribution with parameters and . Is and even, so is the clear median. ${\displaystyle p=1/2}$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle 1/2(n-1)\leq m\leq 1/2(n+1)}$ ${\displaystyle p}$ ${\displaystyle n}$ ${\displaystyle p=1/2}$ ${\displaystyle n}$ ${\displaystyle m=n/2}$

Accumulators

The function generating cumulants is analogous to the Bernoulli distribution

${\displaystyle g_{X}(t)=n\ln(pe^{t}+q)}$.

Therewith the first cumulants are and the recursion equation applies ${\displaystyle \kappa _{1}=np,\kappa _{2}=npq}$

${\displaystyle \kappa _{k+1}=p(1-p){\frac {d\kappa _{k}}{dp}}.}$

Characteristic function

The characteristic function has the form

${\displaystyle \phi _{X}(s)=\left(\left(1-p\right)+p\mathrm {e} ^{\mathrm {i} s}\right)^{n}=\left(q+p\mathrm {e} ^{\mathrm {i} s}\right)^{n}.}$

Probability generating function

For the probability generating function one obtains

${\displaystyle g_{X}(s)=(ps+(1-p))^{n}.}$

Moment generating function

The moment-generating function of the binomial distribution is

${\displaystyle {\begin{aligned}m_{X}(s)&=\operatorname {E} \left(e^{sX}\right)\\&=\sum _{X=0}^{n}\mathrm {e} ^{sX}\cdot {\binom {n}{X}}p^{X}(1-p)^{n-X}\\&=\sum _{X=0}^{n}{\binom {n}{X}}(\mathrm {e} ^{s}p)^{X}(1-p)^{n-X}\\&=\left(p\cdot \mathrm {e} ^{s}+\left(1-p\right)\right)^{n}.\end{aligned}}}$

Sum of binomially distributed random variables

For the sum of two independent binomially distributed random variables and with the parameters , and , the individual probabilities are obtained by applying the Vandermonde identity ${\displaystyle Z=X+Y}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle n_{1}}$ ${\displaystyle p}$ ${\displaystyle n_{2}}$ ${\displaystyle p}$

${\displaystyle {\begin{aligned}\operatorname {P} (Z=k)&=\sum _{i=0}^{k}\left[{\binom {n_{1}}{i}}p^{i}(1-p)^{n_{1}-i}\right]\left[{\binom {n_{2}}{k-i}}p^{k-i}(1-p)^{n_{2}-k+i}\right]\\&={\binom {n_{1}+n_{2}}{k}}p^{k}(1-p)^{n_{1}+n_{2}-k}\qquad (k=0,1,\dotsc ,n_{1}+n_{2}),\end{aligned}}}$

so again a binomial random variable, but with the parameters and . Thus applies to the convolution ${\displaystyle n_{1}+n_{2}}$ ${\displaystyle p}$

${\displaystyle \operatorname {Bin} (n,p)*\operatorname {Bin} (m,p)=\operatorname {Bin} (n+m,p)}$

The binomial distribution is therefore reproductive for fixed or forms a convolution half-group . ${\displaystyle p}$

If the sum is known, each of the random variables and under this condition follows a hypergeometric distribution. To do this, one calculates the conditional probability : ${\displaystyle Z=X+Y}$ ${\displaystyle X}$ ${\displaystyle Y}$

${\displaystyle {\begin{aligned}P(X=\ell |Z=k)&={\frac {P(X=\ell \cap Z=k)}{P(Z=k)}}\\&={\frac {P(X=\ell \cap Y=k-\ell )}{P(Z=k)}}\\&={\frac {P(X=\ell )P(Y=k-\ell )}{P(Z=k)}}\\&={\frac {{\binom {n_{1}}{\ell }}p^{\ell }(1-p)^{n_{1}-\ell }{\binom {n_{2}}{k-\ell }}p^{k-\ell }(1-p)^{n_{2}-k+\ell }}{{\binom {n_{1}+n_{2}}{k}}p^{k}(1-p)^{n_{1}+n_{2}-k}}}\\&={\frac {{\binom {n_{1}}{\ell }}{\binom {n_{2}}{k-\ell }}}{\binom {n_{1}+n_{2}}{k}}}\\&=h(\ell ;n_{1}+n_{2};n_{1};k)\end{aligned}}}$

This represents a hypergeometric distribution .

In general, if the random variables are stochastically independent and satisfy the binomial distributions , then the sum is also binomially distributed, but with the parameters and . Adding binomial random variables with , then we obtain a generalized binomial distribution . ${\displaystyle m}$ ${\displaystyle X_{i}}$ ${\displaystyle B(n_{i},p)}$ ${\displaystyle X_{1}+X_{2}+\dotsb +X_{m}}$ ${\displaystyle n_{1}+n_{2}+\dotsb +n_{m}}$ ${\displaystyle p}$ ${\displaystyle X_{1},X_{2}}$ ${\displaystyle p_{1}\neq p_{2}}$

Relationship to other distributions

Relationship to the Bernoulli distribution

A special case of the binomial distribution for is the Bernoulli distribution . The sum of independent and identical Bernoulli-distributed random variables is therefore sufficient for the binomial distribution. ${\displaystyle n=1}$

Relationship to the generalized binomial distribution

The binomial distribution is a special case of the generalized binomial distribution with for all . More precisely, it is the generalized binomial distribution with maximum entropy for a fixed expectation value and a fixed order . ${\displaystyle p_{i}=p_{j}}$ ${\displaystyle i,j\in \{1,\dotsc ,n\}}$

Transition to normal distribution

According to Moivre-Laplace's theorem , the binomial distribution converges in the limit to a normal distribution , i.e. That is, the normal distribution can be used as a useful approximation of the binomial distribution if the sample size is sufficiently large and the proportion of the desired expression is not too small. With the Galton board one can experience the approximation to the normal distribution. ${\displaystyle n\to \infty }$

It is true and by inserting it into the distribution function the standard normal distribution follows ${\displaystyle \mu =np}$ ${\displaystyle \sigma ^{2}=npq.}$ ${\displaystyle \Phi }$

${\displaystyle B(k\mid p,n)\approx \Phi \left({k+0{,}5-np \over {\sqrt {npq}}}\right)-\ \Phi \left({k-0{,}5-np \over {\sqrt {npq}}}\right)\approx {1 \over {\sqrt {npq}}}\cdot \ {\frac {1}{\sqrt {2\pi }}}\,\cdot \ \exp \left(-{{(k-np)}^{2} \over 2npq}\right).}$

As can be seen, the result is nothing more than the function value of the normal distribution for , as well as (which can also be visualized as the area of ​​the -th strip of the histogram of the standardized binomial distribution with its width and its height). The approximation of the binomial distribution to the normal distribution is used in the normal approximation in order to quickly determine the probability of many levels of the binomial distribution, especially if there are no table values ​​(any longer) for these. ${\displaystyle x=k}$ ${\displaystyle \mu =n\cdot p}$ ${\displaystyle \sigma ^{2}=n\cdot p\cdot q}$ ${\displaystyle k}$ ${\displaystyle 1/\sigma }$ ${\displaystyle \Phi ((k-\mu )/\sigma )}$

Transition to the Poisson distribution

An asymptotically asymmetrical binomial distribution, the expectation value of which converges for and against a constant , can be approximated by the Poisson distribution . The value is then the expected value for all binomial distributions considered in the limit value formation as well as for the resulting Poisson distribution. This approximation is also known as the Poisson approximation , Poisson's limit theorem or the law of rare events. ${\displaystyle np}$ ${\displaystyle n\rightarrow \infty }$ ${\displaystyle p\rightarrow 0}$ ${\displaystyle \lambda }$ ${\displaystyle \lambda }$

${\displaystyle {\begin{aligned}B(k\mid p,n)&={n \choose k}p^{k}\,(1-p)^{n-k}={\frac {n!}{(n-k)!\,k!}}\left({\frac {np}{n}}\right)^{k}\left(1-{\frac {np}{n}}\right)^{n-k}\\&={\frac {n(n-1)(n-2)\dotsm (n-k+1)}{n^{k}}}\,{\frac {(np)^{k}}{k!}}\left(1-{\frac {np}{n}}\right)^{n-k}\\&=\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)\dotsm \left(1-{\frac {k-1}{n}}\right){\frac {(np)^{k}}{k!}}\left(1-{\frac {(np)}{n}}\right)^{n-k}\\&\to \,{\frac {\lambda ^{k}}{k!}}\mathrm {e} ^{-\lambda },\quad {\text{wenn}}\quad n\to \infty \quad {\text{und}}\quad p\rightarrow 0\end{aligned}}}$

As a rule of thumb, this approximation is useful if and . ${\displaystyle n\geq 50}$ ${\displaystyle p\leq 0{,}05}$

The Poisson distribution is the limit distribution of the binomial distribution for large and small , it is a question of convergence in distribution . ${\displaystyle n}$ ${\displaystyle p}$

Relationship to the geometric distribution

The number of failures up to the first occurrence of success is described by the geometric distribution .

Relationship to the negative binomial distribution

The negative binomial distribution, on the other hand, describes the probability distribution of the number of attempts that are required to achieve a specified number of successes in a Bernoulli process .

Relationship to the hypergeometric distribution

With the binomial distribution, the selected samples are returned to the selected set and can therefore be selected again at a later point in time. In contrast, if the samples are not returned to the population , the hypergeometric distribution is used. The two distributions merge into one another if the size of the population is large and the size of the samples is small . As a rule of thumb, even if the samples are not taken, the binomial distribution can be used instead of the mathematically more demanding hypergeometric distribution, since in this case the two only provide results that differ from one another only insignificantly. ${\displaystyle N}$ ${\displaystyle n}$ ${\displaystyle n/N\leq 0{,}05}$

Relationship to the multinomial distribution

The binomial distribution is a special case of the multinomial distribution .

Relationship to the Rademacher distribution

If binomial distribution is for the parameter and , the scaled sum of Rademacher-distributed random variables can be represented: ${\displaystyle Y}$ ${\displaystyle p=0{,}5}$ ${\displaystyle n}$ ${\displaystyle Y}$ ${\displaystyle n}$ ${\displaystyle X_{1},\dotsc ,X_{n}}$

${\displaystyle Y=0{,}5\left(n+\sum _{i=1}^{n}X_{i}\right)}$

This is particularly the symmetric random walk on used. ${\displaystyle \mathbb {Z} }$

Relationship to the Panjer distribution

The binomial distribution is a special case of the Panjer distribution , which combines the distributions binomial distribution, negative binomial distribution and Poisson distribution in one distribution class.

Relationship to beta distribution

For many applications it is necessary to use the distribution function

${\displaystyle \sum _{i=0}^{k}B(i\mid p,n)}$

to be calculated specifically (for example in statistical tests or for confidence intervals ).

The following relationship to the beta distribution helps here :

${\displaystyle \sum _{i=0}^{k}{\binom {n}{i}}\cdot p^{i}\cdot (1-p)^{n-i}=\operatorname {Beta} (1-p;n-k;k+1)}$

For integer positive parameters and : ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle \operatorname {Beta} (x;a;b)={(a+b-1)! \over (a-1)!\cdot (b-1)!}\int _{0}^{x}u^{a-1}(1-u)^{b-1}\,\mathrm {d} u}$

To the equation

${\displaystyle \sum _{i=0}^{k}{\binom {n}{i}}\cdot p^{i}\cdot (1-p)^{n-i}={n! \over (n-k-1)!\cdot k!}\int _{0}^{1-p}u^{n-k-1}(1-u)^{k}\,\mathrm {d} u}$

to prove, one can proceed as follows:

• The left and right sides are the same for (both sides are equal to 1). ${\displaystyle p=0}$
• The derivatives according to are the same for the left and right side of the equation, namely they are both equal . ${\displaystyle p}$ ${\displaystyle -{n! \over (n-k-1)!\cdot k!}\cdot p^{k}\cdot (1-p)^{n-k-1}}$

Relationship to the beta binomial distribution

A binomial distribution whose parameters are beta-distributed is called a beta binomial distribution . It is a mixed distribution . ${\displaystyle p}$

Relationship to the Pólya distribution

The binomial distribution is a special case of the Pólya distribution (choose ). ${\displaystyle c=0}$

Examples

Symmetrical binomial distribution ( p = 1/2)

• 

  p = 0.5 and n = 4, 16, 64

• 

  Mean value deducted

• 

  Scaling with standard deviation

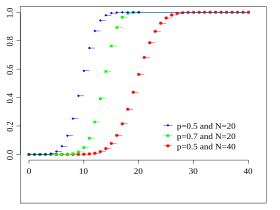
This case occurs when tossing a fair coin twice (probability for heads is the same as for tails, i.e. equal to 1/2). The first figure shows the binomial distribution for and for various values ​​of as a function of . These binomial distributions are mirror symmetrical around the value : ${\displaystyle n}$ ${\displaystyle p=0{,}5}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle k=n/2}$

Binomial distributions with p = 0.5 (with shift by - n / 2 and scaling) for n  = 4, 6, 8, 12, 16, 23, 32, 46

The same data in semi-log plot

${\displaystyle B(k\mid 1/2;n)=B(n-k\mid 1/2;n)}$

This is illustrated in the second figure. The width of the distribution increases proportionally to the standard deviation . The function value at , i.e. the maximum of the curve, decreases proportionally . ${\displaystyle \sigma ={\frac {\sqrt {n}}{2}}}$ ${\displaystyle k=n/2}$ ${\displaystyle \sigma }$

Accordingly, one may binomial distributions with different successive scale by the abscissa by splits and the ordinate with multiplied (third figure above). ${\displaystyle n}$ ${\displaystyle k-n/2}$ ${\displaystyle \sigma }$ ${\displaystyle \sigma }$

The graphic opposite shows once again rescaled binomial distributions, now for other values ​​of and in a plot that better shows that all function values ​​converge towards a common curve with increasing values . By applying the Stirling formula to the binomial coefficients , you can see that this curve (solid black in the picture) is a Gaussian bell curve : ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}\,{\mathrm {e} }^{-{\frac {x^{2}}{2}}}}$.

This is the probability density for the standard normal distribution . In the central limit theorem , this finding is generalized in such a way that sequences of other discrete probability distributions also converge to the normal distribution. ${\displaystyle {\mathcal {N}}(0,1)}$

The second graphic opposite shows the same data in a semi-logarithmic plot. This is recommended if you want to check whether even rare events that deviate from the expected value by several standard deviations follow a binomial or normal distribution.

Pulling bullets

There are 80 balls in a container, 16 of which are yellow. A ball is removed 5 times and then put back again. Because of the replacement, the probability of drawing a yellow ball is the same for all withdrawals, namely 16/80 = 1/5. The value indicates the probability that precisely the balls removed are yellow. As an example we calculate : ${\displaystyle B\left(k\mid {\tfrac {1}{5}};5\right)}$ ${\displaystyle k}$ ${\displaystyle k=3}$

${\displaystyle B\left(3\mid {\tfrac {1}{5}};5\right)={\binom {5}{3}}\cdot \left({\frac {1}{5}}\right)^{3}\cdot \left({\frac {4}{5}}\right)^{2}={\frac {5\cdot 4}{1\cdot 2}}\cdot {\frac {1}{125}}\cdot {\frac {16}{25}}={\frac {64}{1250}}=0{,}0512}$

So in about 5% of the cases you draw exactly 3 yellow balls.

B (k | 0.2; 5)
k	Probability in%
0	0032.768
1	0040.96
2	0020.48
3	0005.12
4th	0000.64
5	0000.032
∑	0100
Adult value	0001
Variance	0000.8

Number of people with birthday on the weekend

The probability that a person's birthday will be on a weekend this year is 2/7 (for the sake of simplicity). There are 10 people in one room. The value indicates (in the simplified model) the probability that exactly those present have a birthday on a weekend this year. ${\displaystyle B(k\mid 2/7;10)}$ ${\displaystyle k}$

B (k | 2/7; 10)
k	Probability in% (rounded)
0	0003.46
1	0013.83
2	0024.89
3	0026.55
4th	0018.59
5	0008.92
6th	0002.97
7th	0000.6797
8th	0000.1020
9	0000.009063
10	0000.0003625
∑	0100
Adult value	0002.86
Variance	0002.04

Common birthday in the year

253 people came together. The value indicates the probability that exactly those present have a birthday on a randomly chosen day (regardless of the year of birth). ${\displaystyle B(k\mid 1/365;253)}$ ${\displaystyle k}$

B (k | 1/365; 253)
k	Probability in% (rounded)
0	049.95
1	034.72
2	012.02
3	002.76
4th	000.47

The likelihood that “anyone” of these 253 people, i.e. H. one or more people who have their birthday on this day is therefore . ${\displaystyle 1-B(0\mid 1/365;253)=50.05\,\%}$

With 252 people the probability is . This means that the threshold for the number of people from which the probability that at least one of these people has a birthday on a randomly chosen day is greater than 50% is 253 people (see also the birthday paradox ). ${\displaystyle 1-B(0\mid 1/365;252)=49.91\,\%}$

Calculating the binomial distribution directly can be difficult due to the large factorials. An approximation using the Poisson distribution is permissible here ( ). ${\displaystyle n>50,p<0{,}05}$The parameter results in the following values: ${\displaystyle \lambda =np=253/365}$

P 253/365 (k)
k	Probability in% (rounded)
0	050
1	034.66
2	012.01
3	002.78
4th	000.48

Confidence interval for a probability

In an opinion poll of people, people say they vote for party A. Determine a 95% confidence interval for the unknown proportion of voters who vote for party A in the total electorate. ${\displaystyle n}$ ${\displaystyle k}$

A solution to the problem without recourse to the normal distribution can be found in the article Confidence Interval for the Success Probability of the Binomial Distribution .

Utilization model

Using the formula can be the probability calculated that of people an activity that on average takes minutes per hour to run simultaneously. ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle m}$

${\displaystyle P(X=k)={n \choose k}\cdot \left({\frac {m}{60}}\right)^{k}\cdot \left(1-{\frac {m}{60}}\right)^{n-k}}$

Statistical error of the class frequency in histograms

The representation of independent measurement results in a histogram leads to the grouping of the measurement values ​​in classes.

The probability for entries in class is given by the binomial distribution ${\displaystyle n_{i}}$ ${\displaystyle i}$

${\displaystyle B_{n,p_{i}}(n_{i})}$with and . ${\displaystyle n=\sum n_{i}}$ ${\displaystyle p_{i}={\frac {n_{i}}{n}}}$

Expectation and variance of are then ${\displaystyle n_{i}}$

${\displaystyle E(n_{i})=np_{i}=n_{i}}$and . ${\displaystyle V(n_{i})=np_{i}(1-p_{i})=n_{i}\left(1-{\frac {n_{i}}{n}}\right)}$

Thus the statistical error of the number of entries in class is at ${\displaystyle i}$

${\displaystyle \sigma (n_{i})={\sqrt {n_{i}\left(1-{\frac {n_{i}}{n}}\right)}}}$.

If there is a large number of classes, and becomes small . ${\displaystyle p_{i}}$ ${\displaystyle \sigma (n_{i})\approx {\sqrt {n_{i}}}}$

In this way, for example, the statistical accuracy of Monte Carlo simulations can be determined.

Random numbers

Random numbers for the binomial distribution are usually generated using the inversion method.

Alternatively, one can also take advantage of the fact that the sum of Bernoulli-distributed random variables is binomially distributed. To do this, one generates Bernoulli-distributed random numbers and adds them up; the result is a binomial distributed random number. ${\displaystyle n}$

Web links

Wikibooks: Binomial Distribution  - Learning and Teaching Materials

Wikibooks: ${\displaystyle {\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}}$  - Mathematics for school

• Bernoulli experiments and binomial distribution
• Calculator for simple and cumulative probabilities of the binomial distribution
• Computing the Binomial Distribution for easy and cumulative probabilities ( English )
• Extensive tables
• Binomial and normal distribution - online tutorial with dynamic worksheets (Java plugin required)
• Interactive coin toss simulation - including tasks (HTML5 without plugin)
• Interactive animation - University of Konstanz (Java plugin required)
• Interactive animation (Flash plugin required)
• Earliest Known Uses of Some of the Words of Probability & Statistics - Kees Verduin.

Individual evidence

1. ↑ Peter Kissel: MAC08 Stochastics (Part 2). Studiengemeinschaft Darmstadt 2014, p. 12.
2. ↑ Bigalke / Köhler: Mathematics 13.2 Basic and advanced course. Cornelsen, Berlin 2000, p. 130.
3. ↑ George Udny Yule : An Introduction to the Theory of Statistics. Griffin, London 1911, p. 287.
4. ↑ Peter Kissel: MAC08 Stochastics (Part 2). Studiengemeinschaft Darmstadt 2014, p. 23.
5. ↑ Bigalke / Köhler: Mathematics 13.2 Basic and advanced course. Cornelsen, Berlin 2000, pp. 144 ff.
6. ↑ P. Neumann: About the median of the binomial and Poisson distribution . In: Scientific journal of the Technical University of Dresden . 19, 1966, pp. 29-33.
7. ↑ Lord, Nick. (July 2010). "Binomial averages when the mean is an integer", The Mathematical Gazette 94, 331-332.
8. ↑ ^{a b} R. Kaas, JM Buhrman: Mean, Median and Mode in Binomial Distributions . In: Statistica Neerlandica . 34, No. 1, 1980, pp. 13-18. doi : 10.1111 / j.1467-9574.1980.tb00681.x .
9. ↑ ^{a b} K. Hamza: The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions . In: Statistics & Probability Letters . 23, 1995, pp. 21-25. doi : 10.1016 / 0167-7152 (94) 00090-U .
10. ↑ Peter Harremoës: Binomial and Poisson Distributions as Maximum Entropy Distributions . In: IEEE Information Theory Society (Ed.): IEEE Transactions on Information Theory . 47, 2001, pp. 2039-2041. doi : 10.1109 / 18.930936 .
11. ↑ M. Brokate, N. Henze, F. Hettlich, A. Meister, G. Schranz-Kirlinger, Th. Sonar: Basic knowledge of mathematics studies: higher analysis, numerics and stochastics. Springer-Verlag, 2015, p. 890.
12. ↑ In the concrete case one has to calculate for the binomial distribution and for the Poisson distribution . Both are easy with the calculator. When calculating with paper and pencil, you need 8 or 9 terms for the value of the Poisson distribution with the exponential series, while for the binomial distribution you get the 256th power by squaring several times and then dividing by the third power. ${\displaystyle \left({\tfrac {364}{365}}\right)^{253}}$ ${\displaystyle e^{-253/365}}$