Binomial coefficient

The binomial coefficient is a mathematical function that can be used to solve one of the basic problems of combinatorics . It indicates how many different ways one can select certain objects from a set of different objects (without replacing, without considering the order). The binomial coefficient is the number of -element subsets of a -element set. ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle n}$

"49 over 6" (or "45 over 6" in Austria and Switzerland) is z. B. the number of possible draws in the lottery (without considering the additional number).

A binomial coefficient depends on two natural numbers and . He will be with the symbol ${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle {\binom {n}{k}}}$

written and spoken as “n over k”, “k out of n” or “n deep k”. The English abbreviation nCr for n choose r can be found on pocket calculators.

These numbers were named because they appear as coefficients in the powers of the binomial ; the so-called binomial theorem applies : ${\displaystyle x+y}$

${\displaystyle {\begin{aligned}(x+y)^{n}&={\binom {n}{0}}x^{n}+{\binom {n}{1}}x^{n-1}y+\dotsb +{\binom {n}{n-1}}xy^{n-1}+{\binom {n}{n}}y^{n}\\&=\sum _{k=0}^{n}{\binom {n}{k}}x^{n-k}y^{k}\end{aligned}}}$

An extension of the binomial coefficient derived from combinatorics is the general binomial coefficient , which is used in analysis .

definition

For a complex number and a nonnegative integer , the binomial coefficient "n over k" is defined as follows: ${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle {\begin{aligned}{\binom {n}{k}}&={\frac {n}{1}}\cdot {\frac {n-1}{2}}\dotsm {\frac {n-(k-1)}{k}}\\&={\frac {n\cdot (n-1)\dotsm (n-k+1)}{k!}}\\&=\prod _{j=1}^{k}{\frac {n+1-j}{j}},\end{aligned}}}$

where denotes the factorial of . The empty product ( ) is included . ${\displaystyle k!}$ ${\displaystyle k}$ ${\displaystyle k=0}$ ${\displaystyle 1}$

If it is a nonnegative integer with , the definition known from combinatorics can be used: ${\displaystyle n}$ ${\displaystyle n\geq k}$

${\displaystyle {\binom {n}{k}}={\frac {n!}{k!\cdot (n-k)!}}}$

properties

If the restriction is also made to non-negative whole numbers, the following applies: ${\displaystyle k}$ ${\displaystyle n}$

• ${\displaystyle {\tbinom {n}{k}}}$is always a nonnegative integer. Is , so is , otherwise is . ${\displaystyle k\leq n}$ ${\displaystyle {\tbinom {n}{k}}\geq 1}$ ${\displaystyle {\tbinom {n}{k}}=0}$
• ${\displaystyle {\binom {n}{0}}=1={\binom {n}{n}}}$
• ${\displaystyle {\binom {n}{1}}=n={\binom {n}{n-1}}}$
• ${\displaystyle {\binom {n}{k}}={\frac {n-k+1}{k}}{\binom {n}{k-1}}}$
• ${\displaystyle {\binom {n}{k}}={\frac {n}{k}}\cdot {\binom {n-1}{k-1}}\Leftrightarrow k\cdot {\binom {n}{k}}=n\cdot {\binom {n-1}{k-1}}}$
• ${\displaystyle {\binom {n+1}{k+1}}={\binom {n}{k}}+{\binom {n}{k+1}}}$. For is the right summand . ${\displaystyle n=k}$ ${\displaystyle {\tbinom {n}{n+1}}=0}$

In the general case of real or complex values ​​for , some of the expressions cited here can become undefined in the sense given above, if namely should no longer be whole and nonnegative; this concerns the statements , and . It turns out, however, that these statements become correct if, in accordance with the analytical generalization below, the beta function is also allowed for complex values. ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle 1={\tbinom {n}{n}}}$ ${\displaystyle n={\tbinom {n}{n-1}}}$ ${\displaystyle {\tbinom {n}{n+1}}=0}$ ${\displaystyle k}$

Symmetry of the binomial coefficients

Binomial integer coefficients are symmetric in the sense of

${\displaystyle {\binom {n}{k}}={\binom {n}{n-k}}}$

for all non-negative and . ${\displaystyle n}$ ${\displaystyle k}$

proof

${\displaystyle {\begin{aligned}{\binom {n}{n-k}}&={\frac {n!}{(n-k)!\cdot (n-(n-k))!}}\\&={\frac {n!}{(n-k)!\cdot k!}}\\&={\frac {n!}{k!\cdot (n-k)!}}\\&={\binom {n}{k}}\end{aligned}}}$

example

${\displaystyle {\binom {5}{3}}={\binom {5}{5-3}}={\binom {5}{2}}}$

${\displaystyle {\binom {5}{3}}={\frac {5!}{3!\cdot (5-3)!}}={\frac {5!}{3!\cdot 2!}}={\frac {1\cdot 2\cdot 3\cdot 4\cdot 5}{(1\cdot 2\cdot 3)\cdot (1\cdot 2)}}={\frac {4\cdot 5}{1\cdot 2}}=10}$

${\displaystyle {\binom {5}{2}}={\frac {5!}{2!\cdot (5-2)!}}={\frac {5!}{2!\cdot 3!}}={\frac {1\cdot 2\cdot 3\cdot 4\cdot 5}{(1\cdot 2)\cdot (1\cdot 2\cdot 3)}}={\frac {4\cdot 5}{1\cdot 2}}=10}$

Recursive representation and Pascal's triangle

For whole numbers and with , the binomial coefficients can also be determined using the following recursion rule: ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle 0\leq k\leq n}$ ${\displaystyle \textstyle {\binom {n}{k}}}$

${\displaystyle {\binom {n}{0}}=1={\binom {n}{n}}}$ for all ${\displaystyle n\geq 0}$

${\displaystyle {\binom {n+1}{k+1}}={\binom {n}{k}}+{\binom {n}{k+1}}}$for everyone and for everyone with ${\displaystyle n>0}$ ${\displaystyle k}$ ${\displaystyle 0\leq k<n}$

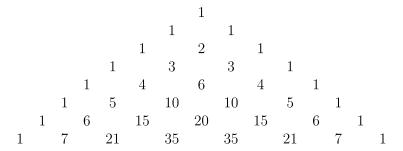
With their help, all binomial coefficients can easily be determined up to a given limit for , a scheme for this is the Pascal triangle : The recursive part there corresponds to the fact that every number is the sum of the two numbers above it. ${\displaystyle n}$

Proof:

${\displaystyle {\begin{aligned}{\binom {n}{k}}+{\binom {n}{k+1}}&={\frac {n!}{k!\cdot (n-k)!}}+{\frac {n!}{(k+1)!\cdot (n-(k+1))!}}\\[.5em]&={\frac {(k+1)\cdot n!}{(k+1)\cdot k!\cdot (n-k)!}}+{\frac {n!\cdot (n-k)}{(k+1)!\cdot (n-k-1)!\cdot (n-k)}}\\[.5em]&={\frac {(k+1)\cdot n!}{(k+1)!\cdot (n-k)!}}+{\frac {n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}}\\[.5em]&={\frac {(k+1)\cdot n!+n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}}\\[.5em]&={\frac {n!\cdot ((k+1)+(n-k))}{(k+1)!\cdot (n-k)!}}\\[.5em]&={\frac {n!\cdot (n+1)}{(k+1)!\cdot (n-k)!}}\\[.5em]&={\frac {(n+1)!}{(k+1)!\cdot ((n+1)-(k+1))!}}\\[.5em]&={\binom {n+1}{k+1}}\end{aligned}}}$

The coefficient can be found in the -th line at the -th position (both counting from zero!): ${\displaystyle {\tbinom {n}{k}}}$ ${\displaystyle n}$ ${\displaystyle k}$

The same triangle represented in the -inomial symbols: ${\displaystyle {\tbinom {n}{k}}}$

${\displaystyle {\tbinom {0}{0}}}$
${\displaystyle {\tbinom {1}{0}}\quad {\tbinom {1}{1}}}$
${\displaystyle {\tbinom {2}{0}}\quad {\tbinom {2}{1}}\quad {\tbinom {2}{2}}}$
${\displaystyle {\tbinom {3}{0}}\quad {\tbinom {3}{1}}\quad {\tbinom {3}{2}}\quad {\tbinom {3}{3}}}$
${\displaystyle {\tbinom {4}{0}}\quad {\tbinom {4}{1}}\quad {\tbinom {4}{2}}\quad {\tbinom {4}{3}}\quad {\tbinom {4}{4}}}$
${\displaystyle {\tbinom {5}{0}}\quad {\tbinom {5}{1}}\quad {\tbinom {5}{2}}\quad {\tbinom {5}{3}}\quad {\tbinom {5}{4}}\quad {\tbinom {5}{5}}}$
${\displaystyle {\tbinom {6}{0}}\quad {\tbinom {6}{1}}\quad {\tbinom {6}{2}}\quad {\tbinom {6}{3}}\quad {\tbinom {6}{4}}\quad {\tbinom {6}{5}}\quad {\tbinom {6}{6}}}$
${\displaystyle {\tbinom {7}{0}}\quad {\tbinom {7}{1}}\quad {\tbinom {7}{2}}\quad {\tbinom {7}{3}}\quad {\tbinom {7}{4}}\quad {\tbinom {7}{5}}\quad {\tbinom {7}{6}}\quad {\tbinom {7}{7}}}$

Algorithm for efficient calculation

For integers, there is an efficient algorithm that uses the product formula ${\displaystyle n}$

${\displaystyle {n \choose k}=\prod _{i=1}^{k}{\frac {n-k+i}{i}}}$

of the binomial coefficient. Due to the constant change between multiplication and division, the intermediate results do not grow unnecessarily. In addition, all intermediate results are also natural numbers.

In order to avoid unnecessary computational effort, the binomial coefficient is calculated in the case : ${\displaystyle k>n/2}$

${\displaystyle {n \choose n-k}={n \choose k}}$

The following pseudocode clarifies the calculation:

binomialkoeffizient(n, k)
1  wenn 2*k > n dann k = n-k
2  ergebnis = 1
3  für i = 1 bis k
4      ergebnis = ergebnis * (n - k + i) / i
5  rückgabe ergebnis

Pocket calculators also use this calculation method if they offer the function. Otherwise the computing capacity would be exhausted. The labeling of the function key with nCr describes the order of the input values ​​in infix notation ; first the number of elements n, then the function key Combinations, then the number of selected objects r ( referred to as k in the article ). ${\displaystyle n=69}$

The calculation nPr ( permutations ) takes into account the permutations of the r elements, the division by is omitted: ${\displaystyle r!}$

${\displaystyle P(n,r)={\frac {n!}{(n-r)!}}}$.

The binomial coefficient in combinatorics

In combinatorial counting there are

${\displaystyle {\binom {n}{k}}={\frac {n!}{k!\cdot (n-k)!}}}$

the number of combinations without repetition of elements of elements. Due to this property, the binomial coefficient plays a central role in combinatorics and is used in the calculation and in the formulas of other combinatorial quantities. ${\displaystyle k}$ ${\displaystyle n}$

Illustration with quantities

Compare also: Combination (combinatorics) → Set representation

Another interpretation of combinations without repetition of k out of n elements is the number of all -element subsets of a -element set. ${\displaystyle k}$ ${\displaystyle n}$

It can be interpreted as follows:

version 1

First one counts all - tuples with pairwise different elements, which can be put together from the -element initial set. There are options for choosing the first tuple element. After any choice of this first, there are only options for the second element, after its selection only for the third, etc., up to options for the -th and last tuple element. The number of all tuples put together in this way is therefore the product of factors, which can also be noted as with the help of the faculty . Now, however, exactly each of the counted -Tuples are permutations of each other and therefore correspond to one and the same -element subset. After dividing by this “counting multiplicity”, the result is actually the number of subsets sought. ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n-1}$ ${\displaystyle n-2}$ ${\displaystyle n-k+1}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle n\cdot (n-1)\cdot (n-2)\dotsm (n-k+2)\cdot (n-k+1)}$ ${\displaystyle k}$ ${\displaystyle {\tfrac {n!}{(n-k)!}}}$ ${\displaystyle k!}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle {\tfrac {n!}{k!\cdot (n-k)!}}={\tbinom {n}{k}}}$

Variant 2

Another, more symmetrical illustration does not emphasize the act of selecting from elements, but rather the aspect of breaking it down into two subsets of and elements. Assume that an -element output tuple consists of red and white elements that are somehow lined up. If one forms all permutations of this sequence, they are each indistinguishable in terms of color, because permutations of the red elements with one another do not change anything in the color sequence, just as little as ever independent permutations within the white ones. So there are only color sequences of the length with all possible different assignments with red elements. Each sequence can now be uniquely assigned to one of the -element subsets of a -element set. The same applies because of the symmetry of red and white or of and also for the complementary -element subsets. The total number of these subsets is thus each . ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle l:=n-k}$ ${\displaystyle n=l+k}$ ${\displaystyle k}$ ${\displaystyle l}$ ${\displaystyle (k+l)!}$ ${\displaystyle k!\cdot l!}$ ${\displaystyle k!}$ ${\displaystyle l!}$ ${\displaystyle {\tfrac {(k+l)!}{k!\cdot l!}}={\tbinom {k+l}{k}}={\tbinom {k+l}{l}}}$ ${\displaystyle k+l}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k+l}$ ${\displaystyle k}$ ${\displaystyle l}$ ${\displaystyle l}$ ${\displaystyle {\tbinom {k+l}{k}}={\tbinom {n}{k}}={\tbinom {n}{n-k}}={\tbinom {k+l}{l}}}$

example

The following applies to the number of possible draws or tickets for the German Lotto 6 out of 49 (without additional number or super number):

${\displaystyle {\tbinom {49}{6}}=13.983.816\approx 14\ {\text{Millionen}}}$

Obviously there is exactly one way to pick 6 correct numbers. counts the possibilities for 0 correct ones, namely to choose all 6 tips from the 43 wrong ones. The number of different tips with 5 correct numbers is very simple , because there are 6 ways to pick just 5 of the 6 numbers drawn (or to omit one of them), and then in each case there are ways to place the omitted tip on one of the 43 wrong numbers . In general, the number of different tips with correct ones results in 6 from 49 with the same consideration . At 6, 0 and 5 right one hardly notices that the factors used , and actually simple binomial coefficients. The sum of all the tip numbers mentioned gives the total number of 13983816 of all possible tips - this follows from the Vandermonde identity given below . ${\displaystyle {\tbinom {43}{6}}}$ ${\displaystyle 6\cdot 43=258}$ ${\displaystyle 43=49-6}$ ${\displaystyle r}$ ${\displaystyle {\tbinom {6}{r}}\cdot {\tbinom {43}{6-r}}}$ ${\displaystyle 1={\tbinom {6}{6}}={\tbinom {6}{0}}={\tbinom {43}{0}}}$ ${\displaystyle 6={\tbinom {6}{5}}}$ ${\displaystyle 43={\tbinom {43}{1}}}$

So the probability of 6 correct numbers with one tip is that of 5 correct numbers . For 0 correct numbers the result is about 44%. The general probability of being correct is a special case of the hypergeometric distribution , which combines three binomial coefficients in this way. ${\displaystyle 1/13983816}$ ${\displaystyle 258/13983816}$ ${\displaystyle 6096454/13983816}$ ${\displaystyle {\tbinom {6}{r}}\cdot {\tbinom {43}{6-r}}/{\tbinom {49}{6}}}$ ${\displaystyle r}$

For more examples, see: Combination (combinatorics) → Examples

Combinatorial Evidence

The combinatorial interpretation also allows simple proofs of relations between binomial coefficients, for example by double counting . Example: For : ${\displaystyle 1\leq k\leq n}$

${\displaystyle {n \choose k}={n-1 \choose k-1}+{n-1 \choose k}}$

Proof: Let it be a -element set and a fixed element. Then the -element subsets of split into two classes: ${\displaystyle X}$ ${\displaystyle n}$ ${\displaystyle x\in X}$ ${\displaystyle k}$ ${\displaystyle X}$

• the subsets that contain; They therefore consist of, together with a -element subset of the -element set , ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle (k-1)}$ ${\displaystyle (n-1)}$ ${\displaystyle X\setminus \{x\}}$
• the subsets that do not contain; they are -element subsets of the -element set . ${\displaystyle x}$ ${\displaystyle k}$ ${\displaystyle (n-1)}$ ${\displaystyle X\setminus \{x\}}$

Combination quantities

The set of all -element subsets of a set is sometimes also referred to because of its power . So for every finite set : ${\displaystyle k}$ ${\displaystyle M}$ ${\displaystyle {\tbinom {\left|M\right|}{k}}}$ ${\displaystyle {\tbinom {M}{k}}}$ ${\displaystyle M}$

${\displaystyle \left|{M \choose k}\right|={\left|M\right| \choose k}}$

Expressions with binomial coefficients

Sums with binomial coefficients

${\displaystyle \sum _{k=0}^{n}{\binom {n}{k}}={\binom {n}{0}}+{\binom {n}{1}}+\dotsb +{\binom {n}{n}}=2^{n}}$

This formula is based on a combinatorial fact. Since the total number of -element subsets of is -element amount, the number is given by the summation of all its subsets, so . The formula can also be derived from the binomial theorem by putting. ${\displaystyle {\tbinom {n}{k}}}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle 2^{n}}$ ${\displaystyle x=y=1}$

Sums with alternating binomial coefficients

${\displaystyle \sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}={\binom {n}{0}}-{\binom {n}{1}}+{\binom {n}{2}}\mp \dotsb +(-1)^{n}{\binom {n}{n}}=0}$for . ${\displaystyle n>0}$

This formula follows for odd from the symmetry of the binomial coefficient. For any it can be derived from the binomial theorem by setting and (or and ). ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle x=1}$ ${\displaystyle y=-1}$ ${\displaystyle x=-1}$ ${\displaystyle y=1}$

Sums of binomial coefficients with even or odd numbers of selected objects

By subtraction or addition to the above equations and followed by halving for get: ${\displaystyle \textstyle \sum _{k=0}^{n}{\binom {n}{k}}=2^{n}}$ ${\displaystyle \textstyle \sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}=0}$ ${\displaystyle n>0}$

${\displaystyle \sum _{k=0}^{[{\frac {n}{2}}]}{\binom {n}{2k}}=2^{n-1}}$like also ; ${\displaystyle \sum _{k=0}^{[{\frac {n-1}{2}}]}{\binom {n}{2k+1}}=2^{n-1}}$

where [] are Gaussian brackets .

Sum of shifted binomial coefficients

Starting from the induction start for anything that uses the recursion rule for binomial coefficients, it is easy to prove with induction after using the recursion rule again: ${\displaystyle \textstyle \sum _{k=0}^{m=1}{\binom {n+k}{n}}={\binom {n}{n}}+{\binom {n+1}{n}}={\binom {n+1}{n+1}}+{\binom {n+1}{n}}={\binom {n+1+1}{n+1}}}$ ${\displaystyle n}$ ${\displaystyle m}$

${\displaystyle \sum _{k=0}^{m}{\binom {n+k}{n}}={\binom {n}{n}}+{\binom {n+1}{n}}+\dotsb +{\binom {n+m}{n}}={\binom {n+m+1}{n+1}}}$;

because of the symmetry of the summands as well as the sum, the following also applies:

${\displaystyle \sum _{k=0}^{m}{\binom {n+k}{k}}={\binom {n}{0}}+{\binom {n+1}{1}}+\dotsb +{\binom {n+m}{m}}={\binom {n+m+1}{m}}={\binom {n+m+1}{n+1}}}$.

Vandermonde identity

${\displaystyle \sum _{j=0}^{k}{\binom {m}{j}}{\binom {n}{k-j}}={\binom {m+n}{k}}.}$

There is also a combinatorial argument here: The right-hand side corresponds to the number of -element subsets of a -element set of spheres. One can now imagine that the balls have two different colors: balls are red and balls green. A subset of elements then consists of a certain number of red balls and many green ones. For each possible , the corresponding summand on the left gives the number of possibilities for such a division into red and green spheres. The sum provides the total number. A proof that is often perceived as simple uses the binomial theorem in the form ${\displaystyle k}$ ${\displaystyle (m+n)}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle j}$ ${\displaystyle k-j}$ ${\displaystyle j}$

${\displaystyle (1+x)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}x^{k},}$

as well as the approach

${\displaystyle (1+x)^{m}(1+x)^{n}=(1+x)^{m+n}}$

and coefficient comparison.

In a special case , Vandermonde's identity results in the following formula for the sums of squares: ${\displaystyle k=m=n}$

${\displaystyle \sum _{j=0}^{n}{\binom {n}{j}}^{2}={\binom {2n}{n}}}$

Divisional remnants

Is a prime number, and , then is ${\displaystyle p}$ ${\displaystyle n_{0},k_{0}\in \{0,\dotsc ,p-1\}}$ ${\displaystyle n_{1},k_{1}\in \mathbb {N} }$

${\displaystyle {\binom {n_{0}+pn_{1}}{k_{0}+pk_{1}}}\equiv {\binom {n_{0}}{k_{0}}}{\binom {n_{1}}{k_{1}}}{\pmod {p}}.}$

That means, modulo can be calculated efficiently with the help of the representations from and to the base , namely “digit by digit”. ${\displaystyle p}$ ${\displaystyle {\tbinom {n}{k}}}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle p}$

Binomial coefficients in analysis

generalization

A generalization that plays a role in calculus is obtained if one allows for an arbitrary complex number , but continues to assume that it is an integer. In this case it is ${\displaystyle n}$ ${\displaystyle \alpha }$ ${\displaystyle k}$

${\displaystyle {\binom {\alpha }{k}}={\begin{cases}{\frac {\alpha (\alpha -1)(\alpha -2)\dotsm (\alpha -(k-1))}{k!}},&{\text{wenn }}\quad k>0\\1,&{\text{wenn }}\quad k=0\\0,&{\text{wenn }}\quad k<0\end{cases}}}$

the binomial coefficient " over " (the empty product in the case is defined as 1). This definition agrees for nonnegative integer with the combinatorial definition (i.e. the definition of as the number of all -element subsets of a fixed -elemental set), and for nonnegative with the algebraic definition (i.e. the definition of as the product ). ${\displaystyle \alpha }$ ${\displaystyle k}$ ${\displaystyle k=0}$ ${\displaystyle \alpha }$ ${\displaystyle {\tbinom {\alpha }{k}}}$ ${\displaystyle k}$ ${\displaystyle \alpha }$ ${\displaystyle k}$ ${\displaystyle {\tbinom {\alpha }{k}}}$ ${\displaystyle {\tfrac {\alpha }{1}}\cdot {\tfrac {\alpha -1}{2}}\dotsm {\tfrac {\alpha -(k-1)}{k}}}$

For example is

${\displaystyle {2{,}5 \choose 2}={\frac {2{,}5\cdot 1{,}5}{2!}}={\frac {3{,}75}{2}}=1{,}875}$

and

${\displaystyle {-1 \choose k}={\frac {(-1)(-2)\dotsm (-k)}{k!}}=(-1)^{k}.}$

The second parameter can also be generalized to any complex assignment if the beta function is used to define: ${\displaystyle k}$ ${\displaystyle z}$ ${\displaystyle \mathrm {B} (x,y)}$ ${\displaystyle \alpha \in \mathbb {C} \setminus \{-1,-2,-3,\dotsc \}}$

${\displaystyle {\binom {\alpha }{z}}={\frac {1}{(\alpha +1)\,\mathrm {B} (z+1,\alpha -z+1)}}={\frac {\Gamma (\alpha +1)}{\Gamma (z+1)\,\Gamma (\alpha -z+1)}},}$

where denotes the gamma function . If there is or is a negative integer, then the value on the right-hand side is 0 because the non-positive integers are the (only) poles of . ${\displaystyle \Gamma (z)}$ ${\displaystyle z}$ ${\displaystyle \alpha -z}$ ${\displaystyle \Gamma (z)}$

Obviously, the symmetry relationship still applies

${\displaystyle {\binom {\alpha }{z}}={\binom {\alpha }{\alpha -z}}}$,

in particular

${\displaystyle {\binom {\alpha }{1}}={\binom {\alpha }{\alpha -1}}=\alpha }$,

${\displaystyle {\binom {\alpha }{0}}={\binom {\alpha }{\alpha }}=1}$

and with a non-negative whole ${\displaystyle m}$

${\displaystyle {\binom {\alpha }{-m}}={\binom {\alpha }{\alpha +m}}=0}$.

In order to extract the sign from the first parameter, provided it is an integer, the relation

${\displaystyle {\binom {-\alpha }{k}}=(-1)^{k}{\binom {\alpha +k-1}{k}}}$

specify.

Generally, for complex , the relationship ${\displaystyle \alpha }$ ${\displaystyle z}$

${\displaystyle {\binom {-\alpha }{z}}=\left(\cos(\pi z)+\sin(\pi z)\cot(\pi \alpha )\right){\binom {\alpha +z-1}{z}}}$.

The multinomial coefficients , which are required when generalizing the binomial to the multinomial theorem , offer a further generalization .

Binomial series

For and with you maintain the relationship ${\displaystyle n\in \mathbb {N} _{0}}$ ${\displaystyle z\in \mathbb {C} \setminus \{1\}}$ ${\displaystyle |z|\geq 1}$

${\displaystyle \sum _{k=0}^{\infty }{\binom {k}{n}}{\frac {1}{z^{k+1}}}=\sum _{k=n}^{\infty }{\binom {k}{n}}{\frac {1}{z^{k+1}}}={\frac {1}{(z-1)^{n+1}}},}$

which is a generalization of the geometric series and belongs to the binomial series .

If , as well as , the following series converges according to ${\displaystyle |z|\leq 1}$ ${\displaystyle z\neq -1}$ ${\displaystyle \alpha \in \mathbb {C} }$

${\displaystyle \sum _{k=0}^{\infty }{\binom {\alpha }{k}}z^{k}=(1+z)^{\alpha }.}$

More exact conditions for and are given in the article Binomial Series . ${\displaystyle z}$ ${\displaystyle \alpha }$

Sum expression for the beta function

Another relationship can be proved for all relatively easily with complete induction, ${\displaystyle m,n\geq 0}$

${\displaystyle \sum \limits _{k=0}^{n}{\binom {n}{k}}{\frac {(-1)^{k}}{m+k+1}}={\dfrac {1}{(m+n+1)\displaystyle {\binom {m+n}{m}}}},}$

from which immediately the symmetry

${\displaystyle \sum \limits _{k=0}^{n}{\binom {n}{k}}{\frac {(-1)^{k}}{m+k+1}}=\sum \limits _{k=0}^{m}{\binom {m}{k}}{\frac {(-1)^{k}}{n+k+1}}}$

follows. A generalization for with and reads ${\displaystyle z,s\in \mathbb {C} }$ ${\displaystyle -z,-s\notin \mathbb {N} }$ ${\displaystyle s+z\neq -1}$

${\displaystyle \sum \limits _{k=0}^{\infty }{\binom {s}{k}}{\frac {(-1)^{k}}{z+k+1}}={\dfrac {1}{(z+s+1)\displaystyle {\binom {z+s}{s}}}}=\mathrm {B} (z+1,s+1).}$

Gaussian product representation for the gamma function

The last formula from the previous section is for ${\displaystyle -z\notin \{0,1,2,\dotsc ,n\}}$

${\displaystyle \sum \limits _{k=0}^{n}{\binom {n}{k}}{\frac {(-1)^{k}}{z+k}}={\frac {n!}{z\,(z+1)\,(z+2)\dotsm (z+n)}}.}$

Looking at the case , replace the fractions in the sum with integrals according to ${\displaystyle \operatorname {Re} z>0}$

${\displaystyle {\frac {1}{z+k}}=\int \limits _{0}^{1}t^{z+k-1}\mathrm {d} t}$

and summarizes the sum of the powers according to the binomial formulas, one obtains

${\displaystyle \sum \limits _{k=0}^{n}{\binom {n}{k}}{\frac {(-1)^{k}}{z+k}}=\int \limits _{0}^{1}t^{z-1}(1-t)^{n}\mathrm {d} t=n^{-z}\int \limits _{0}^{n}t^{z-1}\left(1-{\frac {t}{n}}\right)^{n}\mathrm {d} t,}$

where the substitution was used for the last integral . After all, you have the equation ${\displaystyle t\to t/n}$

${\displaystyle \int \limits _{0}^{n}t^{z-1}\left(1-{\frac {t}{n}}\right)^{n}\mathrm {d} t={\frac {n^{z}\,n!}{z\,(z+1)\,(z+2)\dotsm (z+n)}},}$

from which the Gaussian product representation of the gamma function results directly from the border crossing , ${\displaystyle n\to \infty }$

${\displaystyle \Gamma (z)=\lim \limits _{n\to \infty }{\frac {n^{z}\,n!}{z\,(z+1)\,(z+2)\dotsm (z+n)}},}$

results.

Digammafunction and Euler-Mascheroni constant

For with applies ${\displaystyle m,n\in \mathbb {N} }$ ${\displaystyle m\leq n}$

${\displaystyle \sum \limits _{k=1}^{m}{\binom {n}{m-k}}{\frac {(-1)^{k-1}}{k}}={\binom {n}{m}}\sum \limits _{k=n-m+1}^{n}{\frac {1}{k}},}$

which can also be proven by induction . For the special case this equation is simplified to ${\displaystyle m}$ ${\displaystyle n=m}$

${\displaystyle \sum \limits _{k=1}^{n}{\binom {n}{k}}{\frac {(-1)^{k-1}}{k}}=\sum \limits _{k=1}^{\infty }{\binom {n}{k}}{\frac {(-1)^{k-1}}{k}}=\sum \limits _{k=1}^{n}{\frac {1}{k}}=H_{n},}$

where is the sequence of the harmonic numbers, i.e. the partial sums of the harmonic series . The conversion of the left total into a row (limit instead of ) is allowed because of for ${\displaystyle H_{n}}$ ${\displaystyle \infty }$ ${\displaystyle n}$ ${\displaystyle {\tbinom {n}{k}}=0}$ ${\displaystyle n<k.}$

${\displaystyle H_{n}}$ is on the other hand representable as

${\displaystyle H_{n}=\psi (n+1)-\psi (1)=\psi (n+1)+\gamma }$

with the digamma function and the Euler-Mascheroni constant ${\displaystyle \psi (n)}$ ${\displaystyle \gamma .}$

${\displaystyle \psi (n)}$can be continued for complex values - except for negative whole numbers. So you get the row ${\displaystyle z}$

${\displaystyle \sum \limits _{k=1}^{\infty }{\binom {z}{k}}{\frac {(-1)^{k-1}}{k}}=\psi (z+1)+\gamma }$

as a complex interpolation of the sequence of harmonic numbers.

Trivia

The literal translation of " over " into English " over " does not denote the binomial coefficient , but the fraction . " Choose " is correct . ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle {\tbinom {n}{k}}}$ ${\displaystyle {\tfrac {n}{k}}}$ ${\displaystyle n}$ ${\displaystyle k}$

Web links

Wiktionary: binomial coefficient  - explanations of meanings, word origins, synonyms, translations

Wikibooks: Math for Non-Freaks: Binomial Coefficient  - Learning and Teaching Materials

Wikibooks: Algorithm Collection: Statistics: Binomial Coefficient  - Learning and Teaching Materials

Wikibooks: Combinatorial property of the binomial coefficient

Commons : binomial coefficient  - collection of images, videos, and audio files

• Download from BigAl. (Small, free and platform-independent program, among other things for the exact calculation of the binomial coefficient; with source code).
• Online calculation of any binomial coefficient.

Individual evidence

1. ↑ Disquisitiones generales circa seriem infinitam 1 +… . 1813, p. 26 (also in Carl Friedrich Gauß: Werke. Volume 3, p. 145 ).