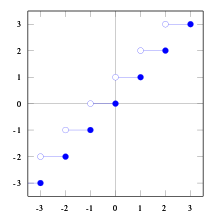
The rounding function (also floor function , integer function , integer part function or Entier Brace ) and the ceiling function are functions that each real number with the closest not greater or is not smaller integer assign. The notation was named after Carl Friedrich Gauß , who introduced the symbol for the rounding function in 1808. End of the 20th century, the spread of Kenneth E. Iverson notation introduced and (Engl. Floor "floor") for the floor function as well and ( English ceiling "ceiling") for the ceiling function. In German, the word Gaussian bracket, without any additional additions, mostly refers to the original notation used by Gauss. The terms lower Gaussian bracket and upper Gaussian bracket are used to differentiate the variants introduced by Iverson .
[
x
]
{\ displaystyle \ left [x \ right]}
floor
(
x
)
{\ displaystyle \ operatorname {floor} (x)}
⌊
x
⌋
{\ displaystyle \ lfloor x \ rfloor}
ceil
(
x
)
{\ displaystyle \ operatorname {ceil} (x)}
⌈
x
⌉
{\ displaystyle \ lceil x \ rceil}
Character set The characters for the rounding and rounding function are further developed square brackets and can be coded as follows in the various environments:
LEFT FLOOR
⌊
U+230A(HTML & # 8970;
& lfloor;)
RIGHT FLOOR
⌋
U+230B(HTML & # 8971;
& rfloor;)
LEFT CEILING
⌈
U+2308(HTML & # 8968;
& lceil;)
RIGHT CEILING
⌉
U+2309(HTML & # 8969;
& rceil;)
In the LaTeX typesetting system , these characters can be specified as \lfloor, \rfloor, \lceiland in math mode \rceil.
Rounding function or Gaussian bracket
Rounding function or Gaussian bracket function
definition
For a real number , the largest integer that is less than or equal to is:
x
{\ displaystyle x}
⌊
x
⌋
{\ displaystyle \ lfloor x \ rfloor}
x
{\ displaystyle x}
⌊
x
⌋
: =
Max
{
k
∈
Z
∣
k
≤
x
}
{\ displaystyle \ lfloor x \ rfloor: = \ max \ {k \ in \ mathbb {Z} \ mid k \ leq x \}}
Examples
⌊
2
,
8th
⌋
=
2
{\ displaystyle \ lfloor 2 {,} 8 \ rfloor = 2}
⌊
-
2
,
8th
⌋
=
-
3
{\ displaystyle \ lfloor -2 {,} 8 \ rfloor = -3}
Note that is not about the same . The definition calls for yes , and it is .
⌊
-
2
,
8th
⌋
{\ displaystyle \ lfloor -2 {,} 8 \ rfloor}
-
2
{\ displaystyle -2}
⌊
x
⌋
≤
x
{\ displaystyle \ lfloor x \ rfloor \ leq x}
-
2
>
-
2
,
8th
{\ displaystyle -2> -2 {,} 8}
⌊
-
2
,
2
⌋
=
-
3
{\ displaystyle \ lfloor -2 {,} 2 \ rfloor = -3}
⌊
2
⌋
=
2
{\ displaystyle \ lfloor 2 \ rfloor = 2}
properties
For all true
k
∈
Z
,
x
∈
R.
{\ displaystyle k \ in \ mathbb {Z}, x \ in \ mathbb {R}}
k
≤
⌊
x
⌋
⟺
k
≤
x
{\ displaystyle k \ leq \ lfloor x \ rfloor \ Longleftrightarrow k \ leq x}
It always applies . Where is if and only if is an integer.
⌊
x
⌋
≤
x
<
⌊
x
⌋
+
1
{\ displaystyle \ lfloor x \ rfloor \ leq x <\ lfloor x \ rfloor +1}
⌊
x
⌋
=
x
{\ displaystyle \ lfloor x \ rfloor = x}
x
{\ displaystyle x}
For every whole number and every real number applies
k
{\ displaystyle k}
x
{\ displaystyle x}
⌊
x
+
k
⌋
=
⌊
x
⌋
+
k
{\ displaystyle \ lfloor x + k \ rfloor = \ lfloor x \ rfloor + k}
The following applies to
all real numbers
x
,
y
{\ displaystyle x, y}
⌊
x
⌋
+
⌊
y
⌋
≤
⌊
x
+
y
⌋
≤
⌊
x
⌋
+
⌊
y
⌋
+
1
{\ displaystyle \ lfloor x \ rfloor + \ lfloor y \ rfloor \ leq \ lfloor x + y \ rfloor \ leq \ lfloor x \ rfloor + \ lfloor y \ rfloor +1}
The following applies to
every whole number and every natural number
k
{\ displaystyle k}
n
{\ displaystyle n}
⌊
k
n
⌋
≥
k
-
n
+
1
n
{\ displaystyle \ left \ lfloor {\ frac {k} {n}} \ right \ rfloor \ geq {\ frac {k-n + 1} {n}}}
The rounding function is idempotent : it applies
⌊
⌊
x
⌋
⌋
=
⌊
x
⌋
{\ displaystyle {\ bigl \ lfloor} \ lfloor x \ rfloor {\ bigr \ rfloor} = \ lfloor x \ rfloor}
If and are coprime natural numbers, then applies
m
{\ displaystyle m}
n
{\ displaystyle n}
∑
j
=
1
n
-
1
⌊
j
m
n
⌋
=
(
m
-
1
)
(
n
-
1
)
2
{\ displaystyle \ sum _ {j = 1} ^ {n-1} \ left \ lfloor {\ frac {jm} {n}} \ right \ rfloor = {\ frac {(m-1) (n-1) } {2}}}
The rounding function is not continuous , but above- semi- continuous .
For non-integer reals , the Fourier series of the -periodic function converges , and we have
x
{\ displaystyle x}
1
{\ displaystyle 1}
⌊
x
⌋
-
x
{\ displaystyle \ lfloor x \ rfloor -x}
⌊
x
⌋
=
x
-
1
2
+
1
π
∑
k
=
1
∞
sin
(
2
k
π
x
)
k
{\ displaystyle \ lfloor x \ rfloor = x - {\ frac {1} {2}} + {\ frac {1} {\ pi}} \ sum _ {k = 1} ^ {\ infty} {\ frac { \ sin {(2k \ pi x)}} {k}}}
Are and , then applies . It follows directly that if , . Furthermore also applies .
m
∈
Z
{\ displaystyle m \ in \ mathbb {Z}}
n
∈
N
{\ displaystyle n \ in \ mathbb {N}}
⌊
x
+
m
n
⌋
=
⌊
⌊
x
⌋
+
m
n
⌋
{\ displaystyle \ left \ lfloor {\ frac {x + m} {n}} \ right \ rfloor = \ left \ lfloor {\ frac {\ lfloor x \ rfloor + m} {n}} \ right \ rfloor}
m
≠
0
{\ displaystyle m \ neq 0}
⌊
⌊
x
/
m
⌋
n
⌋
=
⌊
x
m
n
⌋
{\ displaystyle \ left \ lfloor {\ frac {\ lfloor x / m \ rfloor} {n}} \ right \ rfloor = \ left \ lfloor {\ frac {x} {mn}} \ right \ rfloor}
⌊
m
n
⌋
=
⌈
m
-
n
+
1
n
⌉
{\ displaystyle \ left \ lfloor {\ frac {m} {n}} \ right \ rfloor = \ left \ lceil {\ frac {m-n + 1} {n}} \ right \ rceil}
The following also applies to real numbers
x
,
y
≥
0
{\ displaystyle x, y \ geq 0}
⌊
x
⌋
⋅
⌊
y
⌋
≤
⌊
x
⋅
y
⌋
{\ displaystyle \ lfloor x \ rfloor \ cdot \ lfloor y \ rfloor \ leq \ lfloor x \ cdot y \ rfloor}
Rounding function definition
For a real number, is the smallest integer that is greater than or equal to .
x
{\ displaystyle x}
⌈
x
⌉
{\ displaystyle \ lceil x \ rceil}
x
{\ displaystyle x}
⌈
x
⌉
: =
min
{
k
∈
Z
∣
k
≥
x
}
{\ displaystyle \ lceil x \ rceil: = \ min \ {k \ in \ mathbb {Z} \ mid k \ geq x \}}
Examples
⌈
2
,
8th
⌉
=
3
{\ displaystyle \ lceil 2 {,} 8 \ rceil = 3}
⌈
2
,
3
⌉
=
3
{\ displaystyle \ lceil 2 {,} 3 \ rceil = 3}
⌈
-
2
,
8th
⌉
=
-
2
{\ displaystyle \ lceil -2 {,} 8 \ rceil = -2}
⌈
2
⌉
=
2
{\ displaystyle \ lceil 2 \ rceil = 2}
properties
It applies analogously .
⌈
⌈
x
⌉
⌉
=
⌈
x
⌉
{\ displaystyle \ lceil \ lceil x \ rceil \ rceil = \ lceil x \ rceil}
Are and , then applies . It follows directly that if , .
m
∈
Z
{\ displaystyle m \ in \ mathbb {Z}}
n
∈
N
{\ displaystyle n \ in \ mathbb {N}}
⌈
x
+
m
n
⌉
=
⌈
⌈
x
⌉
+
m
n
⌉
{\ displaystyle \ left \ lceil {\ frac {x + m} {n}} \ right \ rceil = \ left \ lceil {\ frac {\ lceil x \ rceil + m} {n}} \ right \ rceil}
m
≠
0
{\ displaystyle m \ neq 0}
⌈
⌈
x
/
m
⌉
n
⌉
=
⌈
x
m
n
⌉
{\ displaystyle \ left \ lceil {\ frac {\ lceil x / m \ rceil} {n}} \ right \ rceil = \ left \ lceil {\ frac {x} {mn}} \ right \ rceil}
General properties
Gaussian brackets and decimal places
The following applies to positive numbers:
x
=
⌊
x
⌋
+
frac
(
x
)
{\ displaystyle x = \ lfloor x \ rfloor + \ operatorname {frac} (x)}
The function thereby yields the fractional part with .
frac
(
x
)
{\ displaystyle \ operatorname {frac} (x)}
0
≤
frac
(
x
)
<
1
{\ displaystyle 0 \ leq \ operatorname {frac} (x) <1}
Relationships between the rounding function
It is always therefore the rounding function can be obtained from the Gaussian bracket function by
⌈
x
⌉
+
⌊
-
x
⌋
=
0
{\ displaystyle \ lceil x \ rceil + \ lfloor -x \ rfloor = 0}
⌈
x
⌉
=
-
⌊
-
x
⌋
{\ displaystyle \ lceil x \ rceil = - \ lfloor -x \ rfloor}
It is always
⌈
x
⌉
≤
y
⟺
x
≤
⌊
y
⌋
{\ displaystyle \ left \ lceil x \ right \ rceil \ leq y \ Longleftrightarrow x \ leq \ left \ lfloor y \ right \ rfloor}
⌊
x
⌋
<
y
⟺
x
<
⌈
y
⌉
{\ displaystyle \ left \ lfloor x \ right \ rfloor <y \ Longleftrightarrow x <\ left \ lceil y \ right \ rceil}
The following applies to whole numbers :
k
{\ displaystyle k}
⌊
k
2
⌋
+
⌈
k
2
⌉
=
k
{\ displaystyle \ left \ lfloor {\ frac {k} {2}} \ right \ rfloor + \ left \ lceil {\ frac {k} {2}} \ right \ rceil = k}
Commercial rounding
The commercial rounding to the nearest whole number can also be expressed with these functions:
⌊
x
+
0
,
5
⌋
{\ displaystyle \ lfloor x + 0 {,} 5 \ rfloor}
x
≥
0
{\ displaystyle x \ geq 0}
⌈
x
-
0
,
5
⌉
{\ displaystyle \ lceil x-0 {,} 5 \ rceil}
x
<
0
{\ displaystyle x <0}
The function delivers the same result, albeit with a somewhat more complicated formula, but without differentiating between cases with regard to the sign of the argument
⌊
|
x
|
+
0
,
5
⌋
⋅
so-called
(
x
)
{\ displaystyle \ lfloor | x | +0 {,} 5 \ rfloor \ cdot \ operatorname {sgn} (x)}
Web links Individual evidence
↑ Earliest Uses of Function Symbols : Until recently [x] has been the standard symbol for the greatest integer function. According to Grinstein (1970), "The use of the bracket notation, which has led some authors to term this the bracket function , stems back to the work of Gauss (1808) in number theory. The function is also referred to by Legendre who used the now obsolete notation E (x). " The Gauss reference is to Theorematis arithmetici demonstratio nova . Works Volume: Vol. 2 p. 5. (accessed July 25, 2009).
↑ Earliest Known Uses of Some of the Words of Mathematics (C) : The terms Ceiling Function and appear in Kenneth E. Iverson's A Programming Language (1962, p. 12): “Two functions are defined: 1. the floor of x ( or integral part of x) denoted by and defined as the largest integer not exceeding x, 2. the ceiling of x denoted by and defined as the smallest integer not exceeded by x. " This was the first appearance of the terms and symbols, according to RL Graham , DE Knuth & O. Patashnik Concrete Mathematics: A Foundation for Computer Science (1989, p. 67). (accessed on July 25, 2009).
⌊
x
⌋
{\ displaystyle \ lfloor x \ rfloor}
⌈
x
⌉
{\ displaystyle \ lceil x \ rceil}
^ Max Koecher: Classical elementary analysis . Springer, 2013, ISBN 978-3-0348-5167-1 , p. 115
^ Konrad Königsberger: Analysis 1 . Springer, 3rd edition, 2013, ISBN 978-3-642-97622-3 , p. 28
↑ Jürgen Large: Basic Statistics with R: An application-oriented introduction to the use of statistical software R . Springer, 2010, ISBN 978-3-8348-1039-7 , pp. 33-34
<img src="https://de.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">
![\ left [x \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bee30b48da3d61e9dfa898ca4d209afdcc6503dc)