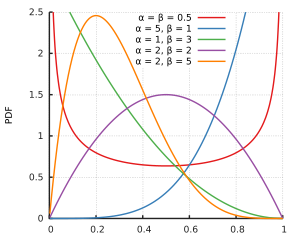
Beta distribution

Beta distribution for different parameter values

Cumulative distribution function for various parameter values

The beta distribution is a family of continuous probability distributions over the interval , parameterized by two parameters, which are often referred to as p and q - or also as α and β . In Bayesian statistics , the beta distribution is the conjugate a priori probability distribution for the Bernoulli, binomial, negative binomial, and geometric distributions. ${\displaystyle (0,1)}$

definition

The beta distribution is defined by the probability density ${\displaystyle \operatorname {Beta} (p,q)}$

${\displaystyle f(x)={\frac {1}{\mathrm {B} (p,q)}}x^{p-1}(1-x)^{q-1}.}$

Outside the interval it is continued with. For can be replaced by . The beta distribution has the real parameters and (in the adjacent graphics and ). In order to guarantee that they can be standardized, (or ) is required. ${\displaystyle (0,1)}$ ${\displaystyle f(x)=0}$ ${\displaystyle p,q\geq 1}$ ${\displaystyle (0,1)}$ ${\displaystyle [0,1]}$ ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle p,q>0}$ ${\displaystyle \alpha ,\beta >0}$

The prefactor is used for correct normalization. The expression ${\displaystyle 1/\mathrm {B} (p,q)}$

${\displaystyle \mathrm {B} (p,q)={\frac {\Gamma (p)\Gamma (q)}{\Gamma (p+q)}}=\int _{0}^{1}u^{p-1}(1-u)^{q-1}\,\mathrm {d} u}$

stands for the beta function after which the distribution is named. The gamma function denotes . ${\displaystyle \Gamma }$

The distribution function is corresponding

${\displaystyle F(x)={\begin{cases}0&{\text{für}}\;x\leq 0,\\I_{x}(p,q)&{\text{für}}\;0<x\leq 1,\\1&{\text{für}}\;x>1\\\end{cases}}}$

With

${\displaystyle I_{x}(p,q):={\frac {1}{\mathrm {B} (p,q)}}\int _{0}^{x}u^{p-1}(1-u)^{q-1}\mathrm {d} u.}$

The function is also called the regularized incomplete beta function . ${\displaystyle I_{x}(p,q)}$

properties

Expected value

The expected value is calculated as

${\displaystyle \operatorname {E} (X)={\frac {p}{p+q}}}$.

mode

The mode , so the maximum point of the density function is for , ${\displaystyle f}$ ${\displaystyle p>1}$ ${\displaystyle q>1}$

${\displaystyle \left(1+{\frac {q-1}{p-1}}\right)^{-1}={\frac {p-1}{p+q-2}}}$.

Variance

The variance results from

${\displaystyle \operatorname {Var} (X)={\frac {pq}{(p+q+1)(p+q)^{2}}}}$.

Standard deviation

For the standard deviation results

${\displaystyle \sigma ={\sqrt {\frac {pq}{(p+q+1)(p+q)^{2}}}}}$.

Coefficient of variation

The coefficient of variation is obtained directly from the expected value and the variance

${\displaystyle \operatorname {VarK} (X)={\sqrt {\frac {q}{p(p+q+1)}}}}$.

Crookedness

The skew arises too

${\displaystyle \operatorname {v} (X)={\frac {2(q-p){\sqrt {p+q+1}}}{(p+q+2){\sqrt {pq}}}}}$.

Higher moments

The torque-generating function results in the k-th moments

${\displaystyle \operatorname {E} (X^{k})=\prod _{r=0}^{k-1}{\frac {p+r}{p+q+r}}}$.

symmetry

The beta distribution is for symmetrical around with the skewness . ${\displaystyle p=q}$ ${\displaystyle x={\frac {1}{2}}}$ ${\displaystyle \operatorname {v} (X)=0}$

Moment generating function

The moment-generating function of a beta-distributed random variable is

${\displaystyle M_{X}(t)=1+\sum _{n=1}^{\infty }\left(\prod _{k=0}^{n-1}{\frac {p+k}{p+q+k}}\right){\frac {t^{n}}{n!}}}$.

The representation is obtained with the hypergeometric function ${\displaystyle _{1}F_{1}}$

${\displaystyle M_{X}(t)={}_{1}F_{1}(p;q;t)}$.

Characteristic function

The characteristic function is obtained analogously to the torque-generating function

${\displaystyle \varphi _{X}(t)={}_{1}F_{1}(p;q;it)}$.

Relationships with other distributions

Special cases

• The constant uniform distribution results as a special case for . ${\displaystyle p=q=1}$
• The arcsin distribution is a special case for . ${\displaystyle p=q={\frac {1}{2}}}$

Relationship to the gamma distribution

If and are independent gamma distributed random variables with parameters and , then the size is beta distributed with parameters and , for short ${\displaystyle X\sim \gamma (p_{1},b)}$ ${\displaystyle Y\sim \gamma (p_{2},b)}$ ${\displaystyle p_{1},b}$ ${\displaystyle p_{2},b}$ ${\displaystyle {\tfrac {X}{X+Y}}}$ ${\displaystyle p_{1}}$ ${\displaystyle p_{2}}$

${\displaystyle \operatorname {Beta} (p_{1},p_{2})\sim {\frac {\gamma (p_{1},b)}{\gamma (p_{1},b)+\gamma (p_{2},b)}}.}$

Relationship to constant uniform distribution

If independent random variables are uniformly distributed, then the order statistics are beta-distributed. More precisely applies ${\displaystyle X_{1},X_{2},\dotsc ,X_{n}}$ ${\displaystyle [0,1]}$ ${\displaystyle X_{(1)},X_{(2)},\dotsc ,X_{(n)}}$

${\displaystyle X_{(k)}\sim \operatorname {Beta} (k,n-k+1)}$

for . ${\displaystyle k=1,\dotsc ,n}$

Mixed distributions

A binomial distribution whose parameters are beta-distributed is called a beta binomial distribution . This is a special case of mixed distribution . ${\displaystyle p}$

example

→ Main article : coefficient of determination

The beta distribution can be determined from two gamma distributions : The quotient of the stochastically independent random variables and , both of which are gamma distributed with the parameters and or , is beta distributed with the parameters and . and can be interpreted as chi-square distributions with or degrees of freedom . ${\displaystyle X=U/(U+V)}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle b}$ ${\displaystyle p_{u}}$ ${\displaystyle p_{v}}$ ${\displaystyle p_{u}}$ ${\displaystyle p_{v}}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle 2p_{u}}$ ${\displaystyle 2p_{v}}$

Using the linear regression is an estimated regression line by a " point cloud " with pairs of values of two statistical features and down, in such a way that the sum of squares of the vertical distances of the values of the straight line is minimized. ${\displaystyle {\hat {y}}={\hat {\beta }}_{0}+{\hat {\beta }}_{1}x_{i}}$ ${\displaystyle n}$ ${\displaystyle \{x_{i};y_{i}\}_{i=1,\dots ,n}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle y_{i}}$ ${\displaystyle {\hat {y}}_{i}}$

The spread of the estimated values around their mean value can be measured by and the dispersion of the measured values around their mean value can be measured by. The former represents the "(by regression) explained sum of squares " ( sum of squares explained ' , in short: SSE ) and the latter is the " total sum of squares " ( sum of squares total , in short SST ) is the. Quotient of these two variables is the coefficient of determination : ${\displaystyle {\hat {y}}_{i}}$ ${\displaystyle {\overline {\hat {y}}}={\overline {y}}}$ ${\displaystyle \textstyle {\text{SSE}}\equiv \sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}}$ ${\displaystyle y_{i}}$ ${\displaystyle \textstyle {\text{SST}}\equiv \sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}$

${\displaystyle {\mathit {R}}^{2}\equiv {\frac {\text{SSE}}{\text{SST}}}}$.

The "non-declared (by regression) square sum" or the " residual sum " ( residual sum of squares , shortly SSR ) is by given. By decomposing the sum of squares , the coefficient of determination can also be represented as ${\displaystyle \textstyle {\text{SSR}}\equiv \sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}$ ${\displaystyle {\text{TSS}}={\text{ESS}}+{\text{RSS}}}$

${\displaystyle {\mathit {R}}^{2}={\frac {\text{SSE}}{{\text{SSE}}+{\text{SSR}}}}}$.

So it's beta distributed. Since the coefficient of determination is the square of the correlation coefficient of and ( ), the square of the correlation coefficient is also beta-distributed. However, the distribution of the coefficient of determination for the global F test can be specified using the F distribution , which is available in a table. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle R^{2}=r^{2}}$

Generalization: Beta distribution on (a, b)

definition

The general beta distribution is defined by the probability density

${\displaystyle f(x)={\frac {1}{B(a,b,p,q)}}(x-a)^{p-1}(b-x)^{q-1},}$

where and are the upper and lower limits of the interval. The calculation of zu results accordingly ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle B}$

${\displaystyle B(a,b,p,q)=\int _{a}^{b}(u-a)^{p-1}(b-u)^{q-1}\mathrm {d} u={\frac {\Gamma (p)\Gamma (q)}{\Gamma (p+q)}}(b-a)^{p+q-1}.}$

properties

Is beta distributed on the interval with parameters , then is ${\displaystyle X}$ ${\displaystyle (0,1)}$ ${\displaystyle p}$ ${\displaystyle q}$

${\displaystyle Y=(b-a)X+a}$

beta distributed on the interval using the same parameters , . Conversely, if beta is distributed to , then is ${\displaystyle (a,b)}$ ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle Y}$ ${\displaystyle (a,b)}$

${\displaystyle X={\frac {Y-a}{b-a}}}$

beta distributed to . ${\displaystyle (0,1)}$

example

In the triangle test , three samples are arranged in an equilateral triangle with one corner of the imaginary triangle pointing upwards. Two of the three samples belong to product A and one sample belongs to product B or vice versa. The test person's task is to find the product that only occurs once. The probability of giving the correct answer by mere guessing is . ${\displaystyle {\tfrac {1}{3}}}$

Distribution of the success probabilities of a sample in the triangular test (black line) with a rate-success probability of (blue line) ${\displaystyle 1/3}$

The chances of success vary depending on sensory skills. Assuming that no test person deliberately gives a wrong answer, the probability of success is not lower for anyone . For gourmets or large differences in taste, this can theoretically increase to 100%. In the following, the beta distribution is derived for any rate-success probabilities using . For the reasons just mentioned, this probability density models the probands' success probabilities more realistically than a beta distribution . ${\displaystyle {\tfrac {1}{3}}}$ ${\displaystyle c}$ ${\displaystyle 0<c<1}$ ${\displaystyle (c,1)}$ ${\displaystyle (0,1)}$

The probabilities of success of the individual test persons are initially beta distributed to with parameters and . The corrected success probabilities on result from . The probability density of can be determined using the transformation theorem for densities . The beta distribution of has a positive density in the interval . The transformation with is a diffeomorphism. This gives the inverse function . For the searched density function of one obtains ${\displaystyle \pi _{i}}$ ${\displaystyle i=1,\dots ,n}$ ${\displaystyle (0,1)}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle (c,1)}$ ${\displaystyle p_{i}=c+(1-c)\pi _{i}}$ ${\displaystyle p_{i}}$ ${\displaystyle \pi _{i}}$ ${\displaystyle (0,1)}$ ${\displaystyle u\colon (0,1)\rightarrow (c,1)}$ ${\displaystyle u(\pi )=c+(1-c)\pi =p}$ ${\displaystyle u^{-1}(p)={\frac {p-c}{1-c}}}$ ${\displaystyle p}$

${\displaystyle f_{p}(p)=f_{\pi }(u^{-1}(p))\left|{\frac {\partial }{\partial p}}u^{-1}(p)\right|=f_{\pi }\left({\frac {p-c}{1-c}}\right)\left|{\frac {1}{1-c}}\right|={\frac {1}{1-c}}f_{\pi }\left({\frac {p-c}{1-c}}|\alpha ,\beta \right)}$.

This probability density of on is shown as a function of the probability density of on . The graph on the right shows an example of a beta distribution with parameters and . The expected value is . The average probability of success is thus higher than the rate-success probability of . ${\displaystyle p}$ ${\displaystyle (c,1)}$ ${\displaystyle \pi }$ ${\displaystyle (0,1)}$ ${\displaystyle ({\tfrac {1}{3}},1)}$ ${\displaystyle \alpha =0{,}5}$ ${\displaystyle \beta =4}$ ${\displaystyle 40{,}7\,\%}$ ${\displaystyle 7{,}4\,\%}$ ${\displaystyle 33{,}3\,\%}$

Individual evidence

1. ↑ Brockhoff, Per Bruun. "The statistical power of replications in difference tests." Food Quality and Preference 14.5 (2003): 405-417.

Web links

• Sigrid Markstein: Mathematical and computational processing of the beta distribution of the 1st type for technological investigations.