Logarithmic normal distribution
The logarithmic normal distribution ( log-normal distribution for short ) is a continuous probability distribution for a variable that can only have positive values. It describes the distribution of a random variable if the random variable transformed with the logarithm is normally distributed . It has proven itself as a model for many measured variables in the natural sciences, medicine and technology, for example for energies, concentrations, lengths and quantities.
In analogy to a normally distributed random variable, which according to the central limit theorem can be understood as the sum of many different random variables, a logarithmically normally distributed random variable arises from the product of many positive random variables. Thus the log-normal distribution is the simplest type of distribution for multiplicative random processes . Since multiplicative laws play a greater role than additive ones in science, economics, and technology, the log-normal distribution is in many applications the one that best fits theory - the second reason why it is often used instead of the usual additive normal distribution should be used.
definition
generation
If is a standard normally distributed random variable, then is log normally distributed with the parameters and , written as . Alternatively, the sizes and can be used as parameters . is a scale parameter. or also determines the form of the distribution.
If there is a log-normal distribution, then there is also a log-normal distribution, with the parameters and or and, respectively . There is also a log-normal distribution, with the parameters and respectively and .
Density function
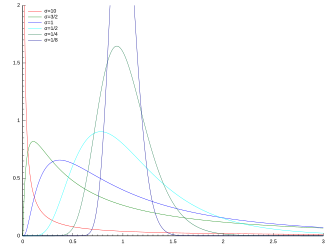
A continuous, positive random variable is subject to a logarithmic normal distribution with the parameters and , if the transformed random variable follows a normal distribution . Your density function is then
- .
Distribution function
This has the log-normal distribution for the distribution function
- ,
where denotes the distribution function of the standard normal distribution .
The distribution function of the logarithmic normal distribution appears on logarithmically divided probability paper as a straight line.
Multidimensional log-normal distribution
Let be a multidimensional (or multivariate) normally distributed random vector. Then there is (i.e. ) multivariate log-normal distribution. The multidimensional log-normal distribution is much less important than the one-dimensional one. Therefore the following text refers almost exclusively to the one-dimensional case.
properties
Quantiles
If the p- quantile of a standard normal distribution (i.e. , where the distribution function is the standard normal distribution), then the p-quantile of the log-normal distribution is given by
- .
Median, multiplicative expected value
The median of the logarithmic normal distribution is accordingly . It is also called the multiplicative or geometric expectation value (see geometric mean ). It is a scale parameter, so the following applies.
Multiplicative standard deviation
Analogous to the multiplicative expected value is the multiplicative or geometric standard deviation. It determines (as well as itself) the form of distribution. It applies .
Since the multiplicative or geometric mean of a sample of lognormal observations (see “Parameter Estimation” below) is itself lognormally distributed, its standard deviation can be stated, which is .
Expected value
The expected value of the logarithmic normal distribution is
- .
Variance, standard deviation, coefficient of variation
The variance results from
- .
For the standard deviation results
- .
The coefficient of variation is obtained directly from the expected value and the variance
- .
Crookedness
The skew arises too
- ,
d. that is, the log-normal distribution is skewed to the right.
The greater the difference between expected value and median, the more pronounced i is. a. the skewness of a distribution. Here these parameters differ by the factor . The probability of extremely large values is therefore high with the log normal distribution with large .
Moments
All moments exist and the following applies:
- .
The moment-generating function and the characteristic function do not exist in explicit form for the log-normal distribution.
entropy
The entropy of the logarithmic normal distribution (expressed in nats ) is
- .
Multiplication of independent, log-normally distributed random variables
Multiplying two independent, log-normally distributed random variables and , then again results in a log-normal random variable with the parameters and , where . The same applies to the product of such variables.
Limit theorem
The geometric mean of independent, equally distributed, positive random variables approximates a log-normal distribution that is more and more similar to an ordinary normal distribution as it decreases.
Expectation value and covariance matrix of a multidimensional log-normal distribution
The expectation vector is
and the covariance matrix
Relationships with other distributions
Relationship to normal distribution
The logarithm of a logarithmically normally distributed random variable is normally distributed. More precisely: If a -distributed real random variable (i.e. normally distributed with expected value and variance ), then the random variable is log-normally distributed with these parameters and .
If and with it goes, the shape of the log-normal distribution goes against that of an ordinary normal distribution.
Distribution with heavy margins
The distribution belongs to the distributions with heavy margins .
Parameter estimation and statistics
Parameter estimation
The parameters are estimated from a sample of observations by determining the mean value and (squared) standard deviation of the logarithmic values:
.
The multiplicative parameters are estimated by and . is the geometric mean . Its distribution is log-normal with a multiplicative expected value and an estimated multiplicative standard deviation (better known as the multiplicative standard error) .
If no individual values are available, but only the mean value and the empirical variance of the non-logarithmic values are known, suitable parameter values are obtained via
- or directly .
statistics
In general, the simplest and most promising statistical analysis of log-normally distributed quantities is carried out in such a way that the quantities are logarithmized and the methods based on the normal normal distribution are used on these transformed values. If necessary, the results, for example confidence or prediction intervals, are then transformed back into the original scale.
The basic example of this is the calculation of dispersion intervals. Since, for an ordinary normal distribution, the probability is around 2/3 (more precisely 68%) and 95% of the probability, the following applies to the log-normal distribution:
- The interval contains 2/3
- and the interval contains 95%
the probability (and thus roughly this percentage of the observations in a sample). The intervals can be noted in analogy to as and .
Such asymmetrical intervals should therefore be shown in graphical representations of (untransformed) observations.
Applications
Variation in many natural phenomena can be described well with the log-normal distribution. This can be explained by the idea that small percentage deviations work together, i.e. the individual effects multiply. This is particularly obvious in the case of growth processes. In addition, the formulas for most of the fundamental laws of nature consist of multiplications and divisions. Additions and subtractions then result on the logarithmic scale, and the corresponding Central Limit Theorem leads to normal distribution - transformed back to the original scale, i.e. to log-normal distribution. This multiplicative version of the limit theorem is also known as Gibrat's law . Robert Gibrat (1904–1980) formulated it for companies.
In some sciences, it is customary to give measured quantities in units that are obtained by taking the logarithm of a measured concentration (chemistry) or energy (physics, technology). The acidity of an aqueous solution is measured by the pH value , which is defined as the negative logarithm of the hydrogen ion activity. A volume is specified in decibels (dB) , which is the ratio of the sound pressure level to a corresponding reference value. The same applies to other energy levels. In financial mathematics, logarithmic values (prices, rates, income) are also often used for calculations, see below.
For such “already logarithmic” quantities, the usual normal distribution is often a good choice; so if one wanted to consider the originally measured quantity, the log-normal distribution would be suitable here.
In general, the log-normal distribution is suitable for measured quantities that can only have positive values, i.e. concentrations, masses and weights, spatial quantities, energies, etc.
The following list shows with examples the wide range of applications of the log-normal distribution.
- Geology : concentration of elements
- Hydrology : The log-normal distribution is useful for the analysis of extreme values such as - for example - monthly or annual maxima of the daily amount of rain or the runoff from water bodies.
- Ecology : The abundance of species often shows a log-normal distribution.
-
Biology and medicine
- Dimensions of the size of living beings (length, skin area, weight);
- Physiological variables such as the blood pressure of men and women. As a consequence, reference ranges for healthy values should be estimated based on a log-normal distribution.
- Incubation periods of infectious diseases;
- In neurology, the distribution of the impulse rate of nerve cells often shows a log-normal form, for example in the cortex and striatum and in the hippocampus and in the entorhinal cortex as well as in other brain regions. Likewise for other neurobiological variables.
- Sensitivity to fungicides ;
- Bacteria on plant leaves:
- Permeability of cell walls and mobility of solutes:
-
Social sciences and economics
- Income distributions show, apart from a few extreme values, an approximate log-normal distribution. (For the top end, the Pareto distribution works well .)
- In financial mathematics , logarithmic returns, prices, etc. are modeled as normally distributed, which means that the original quantities are log-normally distributed. This also applies to the famous Black-Scholes model on which the pricing of options and derivatives is based. However, on closer analysis, the Lévy distribution for the extremely large values may fit better, especially when the stock market crashes .
- Population of cities
- In Internet forums, the length of the comments is log-normally distributed, as is the length of time spent on online articles such as news or jokes.
- The duration of chess games follows a log-normal distribution.
-
technology
- In the modeling of the reliability , repair times are described as log-normal distribution.
- Internet: The file size of publicly available audio and video files is approximately log-normally distributed. The same applies to data traffic.
literature
- Edwin L Crow (Ed.): Lognormal Distributions, Theory and Applications (= Statistics: Textbooks and Monographs), Volume 88. Marcel Dekker, Inc., 1988, ISBN 978-0-8247-7803-3 , pp. Xvi + 387 .
- j Aitchison, JAC Brown: The Lognormal Distribution . Cambridge University Press, 1957.
- Eckhard Limpert, Werner A Stahel, Markus Abbt: PDF Lognormal distributions across the sciences: keys and clues . In: BioScience . 51, No. 5, 2001, pp. 341-352. doi : 10.1641 / 0006-3568 (2001) 051 [0341: LNDATS] 2.0.CO; 2 .
Individual evidence
- ^ Leigh Halliwell: The Lognormal Random Multivariate . In: Casualty Actuarial Society E-Forum, Arlington VA, Spring 2015 ..
- ^ Eckhard Limpert, Werner A Stahel, Markus Abbt: Lognormal distributions across the sciences: keys and clues . In: BioScience . 51, No. 5, 2001, pp. 341-352. doi : 10.1641 / 0006-3568 (2001) 051 [0341: LNDATS] 2.0.CO; 2 .
- ^ Eckhard Limpert, Werner A Stahel: Problems with Using the Normal Distribution - and Ways to Improve Quality and Efficiency of Data Analysis . In: PlosOne . 51, No. 5, 2011, pp. 341-352. doi : 10.1641 / 0006-3568 (2001) 051 [0341: LNDATS] 2.0.CO; 2 .
- ^ John Sutton: Gibrat's Legacy . In: Journal of Economic Literature . 32, No. 1, 1997, pp. 40-59.
- ^ LH Ahrens: The log-normal distribution of the elements (A fundamental law of geochemistry and its subsidiary) . In: Geochimica et Cosmochimica Acta . 5, 1954, pp. 49-73.
- ^ RJ Oosterbaan: 6: Frequency and Regression Analysis . In: HP Ritzema (Ed.): Drainage Principles and Applications, Publication 16 . International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands 1994, ISBN 978-90-70754-33-4 , pp. 175-224.
- ↑ G Sugihara: Minimal community structure: An explanation of species abundance patterns . In: American Naturalist . 116, 1980, pp. 770-786.
- ^ Julian S Huxley: Problems of relative growth . London, 1932, ISBN 978-0-486-61114-3 , OCLC 476909537 .
- ^ Robert W. Makuch, DH Freeman, MF Johnson: Justification for the lognormal distribution as a model for blood pressure . In: Journal of Chronic Diseases . 32, No. 3, 1979, pp. 245-250. doi : 10.1016 / 0021-9681 (79) 90070-5 .
- ↑ PE Sartwell: The incubation period and the dynamics of infectious disease . In: American Journal of Epidemiology . 83, 1966, pp. 204-216.
- ^ Gabriele Scheler, Johann Schumann: Diversity and stability in neuronal output rates . In: 36th Society for Neuroscience Meeting, Atlanta ..
- ↑ Kenji Mizuseki, György Buzsáki: Preconfigured, skewed distribution of firing rates in the hippocampus and entorhinal cortex . In: Cell Reports . 4, No. 5, September 12, 2013, ISSN 2211-1247 , pp. 1010-1021. doi : 10.1016 / j.celrep.2013.07.039 . PMID 23994479 . PMC 3804159 (free full text).
- ↑ György Buzsáki, Kenji Mizuseki: The log-dynamic brain: how skewed distributions affect network operations . In: Nature Reviews. Neuroscience . 15, No. 4, 2017, ISSN 1471-003X , pp. 264-278. doi : 10.1038 / nrn3687 . PMID 24569488 . PMC 4051294 (free full text).
- ↑ Adrien Wohrer, Mark D Humphries, Christian K-making: Population-wide distributions of neural activity during perceptual decision-making . In: Progress in Neurobiology . 103, 2013, ISSN 1873-5118 , pp. 156-193. doi : 10.1016 / j.pneurobio.2012.09.004 . PMID 23123501 . PMC 5985929 (free full text).
- ^ Gabriele Scheler: Logarithmic distributions prove that intrinsic learning is Hebbian . In: F1000 Research . 6, 2017, p. 1222. doi : 10.12688 / f1000research.12130.2 . PMID 29071065 . PMC 5639933 (free full text).
- ^ RA Romero, TB Sutton: Sensitivity of Mycosphaerella fijiensis, causal agent of black sigatoka of banana, to propiconozole . In: Phytopathology . 87, 1997, pp. 96-100.
- ↑ SS Hirano, EV Nordheim, DC Arny, CD Upper: Log-normal distribution of epiphytic bacterial populations on leaf surfaces . In: Applied and Environmental Microbiology . 44, 1982, pp. 695-700.
- ^ P Baur: Log-normal distribution of water permeability and organic solute mobility in plant cuticles . In: Plant, Cell and Environment . 20, 1997, pp. 167-177.
- ^ Fabio Clementi, Mauro Gallegati: Pareto's law of income distribution: Evidence for Germany, the United Kingdom, and the United States . 2005.
- ^ Souma Wataru: Physics of Personal Income . Bibcode: 2002cond.mat..2388S . Retrieved February 22, 2002.
- ^ F Black, M Scholes: The Pricing of Options and Corporate Liabilities . In: Journal of Political Economy . 81, No. 3, 1973, p. 637. doi : 10.1086 / 260062 .
- ^ Benoit Mandelbrot: The (mis-) Behavior of Markets . Basic Books, 2004, ISBN 9780465043552 .
- ↑ Sobkowicz Pawel, et al .: Lognormal distributions of user post lengths in Internet discussions - a consequence of the Weber-Fechner law? . In: EPJ Data Science . 2013.
- ↑ Peifeng Yin, Ping Luo, Wang-Chien Lee, Min Wang: Silence is also evidence: interpreting dwell time for recommendation from psychological perspective . In: ACM International Conference on KDD ..
- ↑ Thomas Ahle: What is the average length of a game of chess? . Retrieved April 14, 2018.
- ↑ Patrick O'Connor Andre Kleyner: Practical Reliability Engineering . John Wiley & Sons, 2011, ISBN 978-0-470-97982-2 , p. 35.
- ^ C Gros, G. Kaczor, D Markovic: Neuropsychological constraints to human data production on a global scale . In: The European Physical Journal B . 85, No. 28, 2012, p. 28. arxiv : 1111.6849 . bibcode : 2012EPJB ... 85 ... 28G . doi : 10.1140 / epjb / e2011-20581-3 .
- ↑ Mohammed Alamsar, George Parisis, Richard Clegg, Nickolay Zakhleniuk: On the distribution of traffic volumes in the Internet and Its Implications . 2019.





















































![{\ displaystyle \ operatorname {E} [{\ boldsymbol {X}}] _ {i} = e ^ {\ mu _ {i} + {\ frac {1} {2}} \ Sigma _ {ii}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4a0389bb62ea69eef66f53a25bec3b03597bd26)
![{\ displaystyle \ operatorname {Var} [{\ varvec {X}}] _ {ij} = e ^ {\ mu _ {i} + \ mu _ {j} + {\ frac {1} {2}} ( \ Sigma _ {ii} + \ Sigma _ {jj})} (e ^ {\ Sigma _ {ij}} - 1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cc764c10dbb0aa65161b9080cddb8a7bf2633f2)














![{\ displaystyle \ quad {\ hat {\ mu}} = \ ln \ left ({\ bar {X}} ^ {2} \ {\ sqrt [{}] {\ frac {1} {{\ hat {\ mathrm {var}}} + {\ bar {X}} ^ {2}}}} \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee9865b53cdf19db90076ba64e736a7bf3cd405)


![{\ displaystyle \ [\ mu ^ {*} / \ sigma ^ {*}, \ mu ^ {*} \ cdot \ sigma ^ {*}] \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8cc1fb208900e6a381cbb185167dc66b6b28d2e)
![{\ displaystyle \ [\ mu ^ {*} / (\ sigma ^ {*}) ^ {2}, \ mu ^ {*} \ cdot (\ sigma ^ {*}) ^ {2}] \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c5b421ac4ed4019ae4548968380ed81a10ac58e)



