Black-Scholes model
The Black-Scholes model (pronounced ˌblæk ˈʃoʊlz ) is a financial mathematical model for evaluating financial options , which was published by Fischer Black and Myron Samuel Scholes in 1973 (after being rejected twice by renowned magazines) and is considered to be a milestone in the financial industry .
history
Robert C. Merton was also involved in the drafting, but published a separate article. In fairness, the model should therefore also bear his name, but this never caught on. However, Merton was honored together with Scholes for the development of this model with the Swedish Reichsbank Prize for Economics in 1997 , Black had died in 1995. However, Black also set different accents than Scholes and Merton.
Model frame
The analysis leading to the Black-Scholes model looks at any derivative that has a non- dividend-paying stock as its underlying .
Assumptions
The original model makes some idealizing assumptions:
- The price of the base value , i.e. the share price, follows a geometric Brownian movement with constant drift and volatility .
- The short sale of financial instruments is possible without restriction.
- There are no transaction costs or taxes. All financial instruments can be traded in any small unit.
- There is no dividend payment on the underlying stock from the time the derivative is closed to maturity .
- There is no risk-free option for arbitrage ( no arbitrage ).
- Financial instruments are traded continuously.
- There is a risk-free interest rate that is constant over time and the same for all terms.
In model extensions, dividend payments, stochastic interest rates or stochastic volatilities are also considered.
Black-Scholes model and Black-Scholes differential equation
The basic idea is to construct a risk-free portfolio from the derivative and the share. In this context, “risk-free” means that the value of the portfolio for short periods of time - synonymous with small changes in the share price - does not depend on the price of the share.
According to the assumptions, the share price moves according to a geometric Brownian movement with incremental price changes
- .
Where is the expected return on the stock price, the volatility and the time. denotes a standard Wiener process . can be viewed as an infinitesimal increase in length over a time interval , i.e. H. as a normally distributed random variable with expected value and variance .
With Itō's lemma one obtains the formula for the changes in the value of a derivative
- .
Here and are the same values as before, since the price of the derivative depends on the price process of the share.
The Wiener process thus influences the share price via a factor and the value of the derivative via a factor . The portfolio that is risk-free in the sense of the analysis therefore consists of
- -1 derivatives ( i.e. a short position in the derivative)
- Pieces of stocks
(Or with the opposite sign: a long position in the derivative and a short position in the stocks of the specified size). In practice, this concept of portfolio hedging is used in the form of delta hedging .
With the given portfolio weights and the price processes for shares and derivatives, the portfolio value and the changes in the portfolio value can be formulated over short periods of time.
The portfolio value is
- ,
i.e. the sum of the negative value of the derivative plus the value of shares. The change in value of the portfolio over short periods of time can be written as
- .
The price changes in the portfolio do not depend on the random price changes in the share price from the Vienna Trial or on the expected return on the share . The second point is an important lesson from the Black-Scholes model.
Since the portfolio is risk-free and, according to assumptions, there are no arbitrage opportunities, the portfolio must generate precisely the risk-free return over short periods of time , i.e.
Substituting this into the last equation gives the Black-Scholes differential equation
- .
Under the given assumptions, this equation is valid for all derivatives that can be defined on the basis of the pricing process for . The type of derivative for which the equation is to be solved determines the boundary conditions for the differential equation.
Black-Scholes option prices
European options produce the capital flows at the end of the term (at )
- for a call
respectively
- for a put
The fair price of the option can be derived from various arguments. It can be shown as the discounted expected value of the payments mentioned in , whereby the expected value is to be formed in relation to the risk-neutral measure. Another way to derive an explicit formula for the option prices is to solve the Black-Scholes differential equation, whereby the payments on maturities are considered as boundary conditions.
Pricing formulas
The Black-Scholes price formula for a European call or put is obtained in both ways:
respectively
in which
denotes the distribution function of the standard normal distribution .
The value of an option is therefore determined by 5 parameters:
- : current share price
- : interest rate congruent with the remaining term of the option
- : The future volatility of the underlying. This is the only unknown variable when the contract is concluded and is therefore ultimately the subject of pricing between the contracting parties.
- : Remaining term of the option with total term at the time
- : Base price, defined as part of the contract
The Greeks according to Black-Scholes
As Greeks ( English Greeks ) are called the partial derivatives of the option price according to the respective model parameters. The advantage of the explicit formula for the option prices - for example in contrast to a numerical solution - is that these derivatives can be calculated easily.
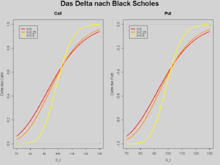
delta
The delta indicates by how much the price of the option changes if the price of the underlying changes by one unit and all other influencing factors remain the same. For example, a "deep in the money" call option has a delta of +1, a "deep in the money" put option of -1.
In the Black-Scholes model, the delta is calculated as:
for the European call, resp.
for the put.
gamma
The gamma is the second derivative of the option price after the price of the underlying asset. It is the same for call and put in the Black-Scholes model
- .
So the gamma is not negative, that is, the option price always changes in the same direction (rise / fall) as the volatility. If the option is in the money (English at the money ), the gamma with decreasing maturity may increase beyond all bounds. The letter stands for the density function of the normal distribution , see distribution function .
Vega (Lambda, Kappa)
Vega, also called lambda or kappa, describes the derivation of the option price according to volatility and thus indicates how strongly an option reacts to changes in volatility (constant in the Black-Scholes model). The Vega is the same for a European call and put, namely
- .
Vega is not a Greek letter . Sigma is already assigned as a symbol for the standard deviation . The volatility is used as an estimate of the future standard deviation.
Theta
The theta denotes the derivative according to the elapsed time t, so it indicates the sensitivity of the option to changes in time. Since, all things being equal , the value of an option approaches the payoff on the maturity date over time, the theta of a European call option is never positive and the option loses value over time. It is also known as the option's time value. In the Black-Scholes model it is
or.
- .
Rho
Rho describes the option's sensitivity to small changes in the interest rate.
- .
omega
The option elasticity is a percentage sensitivity:
- .
application
The Greeks are important for risk management. They make it easier to analyze the influence of individual risk factors. This is particularly true at the level of a portfolio of financial instruments when the influence of individual risk factors - namely the model parameters - on the overall portfolio is to be estimated. An example would be a portfolio of options and positions in the corresponding underlying, e.g. B. Options on the Euro-Bund-Future and Euro-Bund-Future positions as such. The (linear) effect of a change in the futures price on the overall portfolio can be displayed using the delta.
Therefore, the Greeks can also be used for risk protection. The best known example is delta hedging . Using the Rho sensitivity, for example, it can be determined how an option portfolio must be hedged against changes in the refinancing interest rate.
The graphs on the right show the curves with European call values with different remaining terms. These do not overlap and the higher the longer the remaining term. The lowest, kinked curve is the intrinsic value of the option depending on the current base rate today.
- The option values grow monotonically (this does not have to be the case in general, as is the case with interest rate options).
- The price of the European call is always higher than its intrinsic value. In economic terms, this means that it is always better to sell the call on the market than before, because the intrinsic value (today) is smaller than the selling price on the market. This becomes relevant in the case of American calls, as these have an early exercise right. As a general rule, early exercise of American options is worthless as long as it is a non-yielding good (no dividend within the option period).
-
Sensitivity to the price of the underlying asset: Delta : The slope of the tangent to the option value curve corresponds to the delta from the binomial model .
- am Geld ( ): The delta is roughly 1/2. The greater the share price, the greater the slope, the delta.
- deep in the money : the option value reacts like the stock price itself.
-
Sensitivity of the delta with regard to the option price: Gamma : The gamma is the curvature of the curve, the convexity (mathematical: second derivative of the call value according to the share price)
- way out of the money : gamma is close to zero, i. H. the delta remains constant.
- deep in the money : gamma is close to zero.
-
Sensitivity with regard to the term: Theta : Change in the option value when calendar time expires. Shortly before the due date, the call value is extremely time-sensitive and has a high convexity.
- far out of the money : big loss of position
- on the money : medium loss
- deep in the money : big profit
weaknesses
In the Black-Scholes model, the volatility σ is assumed to be constant. However, all ex-post calculations of standard deviations of the returns show that the volatility is not constant over time. Another weakness is that volatility, the most important variable, has to be predicted by oneself. This is done either with the help of regression models by extrapolating past values or by determining the implied volatilities (see there), which could be based on current market prices. The model also includes the simplifying assumption that returns are normally distributed . The normal distribution has little weight at its ends, which means that too little account can be taken of the occurrence of extreme events (see curvature (statistics) ). These limitations of the Black-Scholes model become apparent in the traded prices of options when one considers the volatilities implied by the option prices . The implied volatility for an option on a certain underlying is not constant, but changes over time. In addition, the implied volatility for a certain point in time depends on the closeness to money ("moneyness", see also volatility smile ) and on the remaining term of the option (time structure of the volatility). Both observations do not agree with the model assumption of a uniform, constant volatility. The use of implied volatilities that are dependent on the remaining maturity and the currency are one method of dealing with the limitations of the Black-Scholes model. If another model were to become the standard on the options market instead of the Black-Scholes price formula, it can be assumed that it would not change the traded option prices but rather the volatilities implied by the model.
Advanced models in which volatility is assumed as a falling function of the share price, such as B. the CEV model, give better results.
Derivation
The Black-Scholes model can be interpreted as a borderline case of the time and value discrete binomial model according to Cox, Ross and Rubinstein, in that the trading intervals are set ever shorter:
- .
and lose weight in a controlled manner. The share price returns in the discrete model are binomially distributed. They converge to a normal distribution. The share prices are then logarithmically normally distributed at each point in time. As a rule, a step count of 100 is sufficient with the restriction of exotic options or option sensitivities .
literature
Original work
- Fischer Black , Myron Scholes : The Pricing of Options and Corporate Liabilities. In: Journal of Political Economy. 81, 3, 1973, ISSN 0022-3808 , pp. 637-654.
- Robert C. Merton : Theory of Rational Option Pricing. In: The Bell Journal of Economics and Management Science. 4, 1973, ISSN 0005-8556 , pp. 141-183.
Theoretical criticism
- Nasser Saber: Speculative Capital. Financial Times et al., London 1999
- Vol. 1: The invisible hand of global finance. ISBN 0-273-64155-7 ,
- Vol. 2: The nature of risk in capital markets. ISBN 0-273-64422-X .
Web links
- 1997 Nobel Lectures by Scholes and Merton
- American Mathematical Society ( Memento from April 20, 2005 in the Internet Archive ) for the 97 Nobel Prize in Economics, with further links
- Theory and online calculator (including VAR and the Greeks) of the Black-Scholes option model by Jan-Hendrik Dörner, Goethe University, Frankfurt am Main.
- Bradley University multi-page, informal presentation with extensive bibliography
- Excel macros for calculating the option price
- Hedge Simulator Shows the result of a delta and delta-gamma hedge (replication) in discrete time under a Black-Scholes model.
- Online calculator (including Greeks & source code for download) of the Black-Scholes option model
Individual evidence
- ^ Correct pronunciation of Black-Scholes in Merriam-Webster
- ↑ Mehrling, Perry : "Understanding Fischer Black" first draft of the book chapters that deal with Black's academic years "Fischer Black and the Revolutionary Idea of Finance" ( Memento from June 22, 2010 in the Internet Archive ) (PDF; 158 kB), 2005
- ↑ Representation according to: John C. Hull: Options, futures and other derivatives. 9th ed., Pearson Education, 2015, ISBN 978-0-13-345631-8 , p. 331.
- ↑ The derivation in this section follows: John C. Hull: Options, futures and other derivatives. 9th edition, Pearson Education, 2015, ISBN 978-0-13-345631-8 , pp. 331 ff.
- ↑ Igor Uszczapowski: Understanding Options and Futures. Basics and new developments. 6th updated and expanded edition. Deutscher Taschenbuchverlag, Munich 2008, ISBN 978-3-423-05808-7 ( German. 5808.Beck -Wirtschaftsberater ).
- ^ John C. Hull : Options, Futures, and Other Derivatives. 3rd edition. Prentice Hall International, Upper Saddle River NJ 1997, ISBN 0-13-264367-7 , pp. 503-505, 510f ( Prentice-Hall International Editions ).