Normal distribution
| Normal distribution | |
Density  function Density functions of the normal distribution : (blue), (red), (yellow) and (green) function Density functions of the normal distribution : (blue), (red), (yellow) and (green)
|
|
Distribution  function Distribution functions of the normal distributions: (blue), (red), (yellow) and (green) function Distribution functions of the normal distributions: (blue), (red), (yellow) and (green)
|
|
| parameter |
- Expected value ( location parameter ) - Variance ( scale parameter )
|
|---|---|
| carrier | |
| Density function | |
| Distribution function |
- with error function |
| Expected value | |
| Median | |
| mode | |
| Variance | |
| Crookedness | |
| Bulge | |
| entropy | |
| Moment generating function | |
| Characteristic function | |
| Fisher information | |
The normal or Gauss distribution (after Carl Friedrich Gauß ) is an important type of continuous probability distribution in stochastics . Their probability density function is also called Gaussian function, Gaussian normal distribution, Gaussian distribution curve, Gaussian curve, Gaussian bell curve, Gaussian bell function, Gaussian bell or simply bell curve.
The special importance of the normal distribution is based, among other things, on the central limit theorem , according to which distributions that result from the additive superposition of a large number of independent influences are approximately normally distributed under weak conditions. The family of normal distributions forms a position-scale family .
The deviations of the measured values of many natural, economic and engineering processes from the expected value can be described by the normal distribution (in biological processes often logarithmic normal distribution ) either exactly or at least in a very good approximation (especially processes that are divided into different factors independently of one another Directions act).
Random variables with normal distribution are used to describe random processes such as:
- random scattering of measured values,
- random deviations from the nominal size when manufacturing workpieces,
- Description of Brownian molecular motion .
In actuarial mathematics , the normal distribution is suitable for modeling damage data in the range of medium damage amounts.
In measurement technology , a normal distribution is often used, which describes the spread of the measurement errors. What is important here is how many measuring points are within a certain spread.
The standard deviation describes the width of the normal distribution. The half width of a normal distribution is approximately times (exactly ) the standard deviation. The following applies approximately:
- In the interval of the deviation from the expected value, 68.27% of all measured values can be found,
- In the interval of the deviation from the expected value, 95.45% of all measured values can be found,
- In the interval of the deviation from the expected value, 99.73% of all measured values can be found.
And conversely, the maximum deviations from the expected value can be found for given probabilities:
- 50% of all measured values have a deviation of at most from the expected value,
- 90% of all measured values have a maximum deviation from the expected value,
- 95% of all measured values have a deviation of at most from the expected value,
- 99% of all measured values have a maximum deviation from the expected value.
In addition to the expected value, which can be interpreted as the center of gravity of the distribution, the standard deviation can also be assigned a simple meaning with regard to the magnitude of the probabilities or frequencies that occur.
history

In 1733 Abraham de Moivre showed in his work The Doctrine of Chances in connection with his work on the limit theorem for binomial distributions an estimate of the binomial coefficient, which can be interpreted as a pre-form of the normal distribution. The calculation of the non- elementary integral necessary for normalizing the normal distribution density to the probability density
succeeded Pierre-Simon Laplace in 1782 (according to other sources Poisson ). In 1809, Gauß published his work Theoria motus corporum coelestium in sectionibus conicis solem ambientium ( German theory of the movement of the celestial bodies moving in conic sections around the sun ), which defines the normal distribution in addition to the method of least squares and maximum likelihood estimation . It was also Laplace who in 1810 proved the theorem of the central limit value , which represents the basis of the theoretical meaning of the normal distribution, and who completed de Moivre's work on the limit value theorem for binomial distributions. Adolphe Quetelet finally recognized an astonishing agreement with the normal distribution in investigations of the chest girth of several thousand soldiers in 1844 and brought the normal distribution into the applied statistics . He probably coined the term "normal distribution".
definition
A continuous random variable has a ( Gaussian or) normal distribution with expectation and variance ( ), often written as if it has the following probability density :
- .
The graph of this density function has a “ bell-shaped shape” and is symmetrical with the parameter as the center of symmetry, which also represents the expected value , the median and the mode of distribution. The variance of is the parameter . Furthermore, the probability density has turning points at .
The probability density of a normally distributed random variable has no definite integral that can be solved in closed form , so that probabilities have to be calculated numerically. The probabilities can use a standard normal distribution table are calculated, a standard form used. To see this, one uses the fact that a linear function of a normally distributed random variable is itself normally distributed again. In concrete terms, this means that if and , where and are constants with , then applies . The consequence of this is the random variable
- ,
which is also called the standard normally distributed random variable . The standard normal distribution is the normal distribution with parameters and . The density function of the standard normal distribution is given by
- .
Their course is shown graphically opposite.
The multidimensional generalization can be found in the article Multidimensional Normal Distribution .
properties
Distribution function
The distribution function of the normal distribution is through
given. If one introduces a new integration variable instead of a substitution , the result is
It is the distribution function of the standard normal distribution
The error function can be represented as
- .
symmetry
The probability density graph is a Gaussian bell curve, the height and width of which depends on. It is axially symmetrical to the straight line with the equation and thus a symmetrical probability distribution around its expected value. The graph of the distribution function is point-symmetric to the point For is especially true and for all .
Maximum value and inflection points of the density function
With the help of the first and second derivative , the maximum value and the turning points can be determined. The first derivative is
The maximum of the density function of the normal distribution is therefore at and is there .
The second derivative is
- .
Thus the turning points are included in the density function . The density function has the value at the turning points .
Normalization

It is important that the total area under the curve is equal , i.e. equal to the probability of the certain event . Thus it follows that if two Gaussian bell curves have the same but different one , the curve with the larger one is wider and lower (since both associated surfaces each have the same value and only the standard deviation is larger). Two bell curves with the same but different ones have congruent graphs that are shifted from one another by the difference in the values parallel to the axis.
Every normal distribution is actually normalized, because with the help of linear substitution we get
- .
For the normalization of the latter integral see error integral .
calculation
Since it can not be traced back to an elementary antiderivative , tables were usually used for the calculation in the past (see standard normal distribution table ). Nowadays there are functions available in statistical programming languages such as R , which also master the transformation to arbitrary and .
Expected value
The expected value of the standard normal distribution is . It is true
since the integrand can be integrated and is point-symmetric .
Is now , then is is standard normal distributed, and thus
Variance and other measures of dispersion
The variance of the -normally distributed random variables corresponds to the parameter
- .
An elementary proof is ascribed to Poisson.
The mean absolute deviation is and the interquartile range .
Standard deviation of the normal distribution
One-dimensional normal distributions are fully described by specifying the expected value and variance . So if there is a - -distributed random variable - in symbols - its standard deviation is simple .
Spreading intervals
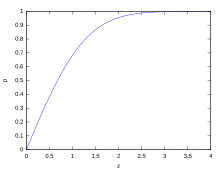
From the standard normal distribution table it can be seen that for normally distributed random variables in each case approximately
- 68.3% of the realizations in the interval ,
- 95.4% in the interval and
- 99.7% in the interval
lie. Since in practice many random variables are almost normally distributed, these values from the normal distribution are often used as a rule of thumb. For example, it is often assumed to be half the width of the interval that encompasses the middle two thirds of the values in a sample, see quantile .
However, this practice is not recommended because it can lead to very large errors. For example, the distribution can hardly be visually differentiated from the normal distribution (see picture), but 92.5% of the values lie in the interval , with the standard deviation of . Such contaminated normal distributions are very common in practice; The example mentioned describes the situation when ten precision machines produce something, but one of them is badly adjusted and produces with deviations ten times as high as the other nine.
Values outside of two to three times the standard deviation are often treated as outliers . Outliers can be an indication of gross errors in data acquisition . However, the data can also be based on a highly skewed distribution. On the other hand, with a normal distribution, on average about every 20th measured value is outside of twice the standard deviation and about every 500th measured value is outside of three times the standard deviation.
Since the proportion of values outside of six times the standard deviation is vanishingly small at approx. 2 ppb , such an interval is a good measure for almost complete coverage of all values. This is used in quality management by the Six Sigma method , in which the process requirements stipulate tolerance limits of at least . However, one assumes a long-term shift in the expected value by 1.5 standard deviations, so that the permissible error portion increases to 3.4 ppm . This proportion of error corresponds to four and a half times the standard deviation ( ). Another problem with the method is that the points cannot be determined in practice. If the distribution is unknown (i.e. if it is not absolutely certain to be a normal distribution), for example, the extreme values of 1,400,000,000 measurements limit a 75% confidence interval for the points.
| Percent within | Percent outside | ppb outside | Fraction outside | |
|---|---|---|---|---|
| 0.674490 | 50% | 50% | 500,000,000 | 1/2 |
| 0.994458 | 68% | 32% | 320,000,000 | 1 / 3.125 |
| 1 | 68,268 9492% | 31,731 0508% | 317.310.508 | 1 / 3.151 4872 |
| 1.281552 | 80% | 20% | 200,000,000 | 1/5 |
| 1.644854 | 90% | 10% | 100,000,000 | 1/10 |
| 1.959964 | 95% | 5% | 50,000,000 | 1/20 |
| 2 | 95.449 9736% | 4,550 0264% | 45.500.264 | 1 / 21,977 895 |
| 2.354820 | 98,146 8322% | 1.853 1678% | 18,531,678 | 1/54 |
| 2.575829 | 99% | 1 % | 10,000,000 | 1/100 |
| 3 | 99.730 0204% | 0.269 9796% | 2,699,796 | 1 / 370.398 |
| 3.290527 | 99.9% | 0.1% | 1,000,000 | 1 / 1,000 |
| 3.890592 | 99.99% | 0.01% | 100,000 | 1 / 10,000 |
| 4th | 99.993 666% | 0.006 334% | 63,340 | 1 / 15,787 |
| 4,417173 | 99.999% | 0.001% | 10,000 | 1 / 100,000 |
| 4.891638 | 99.9999% | 0.0001% | 1,000 | 1 / 1,000,000 |
| 5 | 99.999 942 6697% | 0.000 057 3303% | 573.3303 | 1 / 1,744,278 |
| 5,326724 | 99.999 99% | 0.000 01% | 100 | 1 / 10,000,000 |
| 5,730729 | 99.999 999% | 0.000 001% | 10 | 1 / 100,000,000 |
| 6th | 99.999 999 8027% | 0.000 000 1973% | 1,973 | 1 / 506.797.346 |
| 6.109410 | 99.999 9999% | 0.000 0001% | 1 | 1 / 1,000,000,000 |
| 6,466951 | 99.999 999 99% | 0.000 000 01% | 0.1 | 1 / 10,000,000,000 |
| 6.806502 | 99.999 999 999% | 0.000 000 001% | 0.01 | 1 / 100,000,000,000 |
| 7th | 99.999 999 999 7440% | 0.000 000 000 256% | 0.002 56 | 1 / 390.682.215.445 |
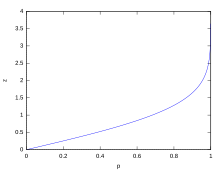
The probabilities for certain scattering intervals can be calculated as
- ,
where is the distribution function of the standard normal distribution .
Conversely, can for given by
the limits of the associated scattering interval can be calculated with probability .
An example (with fluctuation range)
The human body size is approximately normally distributed. In a sample of 1,284 girls and 1,063 boys between the ages of 14 and 18, the girls had an average height of 166.3 cm (standard deviation 6.39 cm) and the boys an average height of 176.8 cm (standard deviation 7.46 cm) measured.
Accordingly, the above fluctuation range suggests that 68.3% of the girls have a height in the range 166.3 cm ± 6.39 cm and 95.4% in the range 166.3 cm ± 12.8 cm,
- 16% [≈ (100% - 68.3%) / 2] of the girls are shorter than 160 cm (and 16% correspondingly taller than 173 cm) and
- 2.5% [≈ (100% - 95.4%) / 2] of the girls are shorter than 154 cm (and 2.5% correspondingly taller than 179 cm).
For boys it can be expected that 68% have a height in the range 176.8 cm ± 7.46 cm and 95% in the range 176.8 cm ± 14.92 cm,
- 16% of boys shorter than 169 cm (and 16% taller than 184 cm) and
- 2.5% of boys are shorter than 162 cm (and 2.5% taller than 192 cm).
Coefficient of variation
The coefficient of variation is obtained directly from the expected value and the standard deviation of the distribution
Crookedness
The skewness has independent of the parameters and getting the value .
Bulge
The vault is also of and independent and equal . In order to better assess the curvature of other distributions, they are often compared with the curvature of the normal distribution. The curvature of the normal distribution is normalized to (subtraction of 3); this size is called excess .
Accumulators
The cumulative generating function is
This is the first cumulant , the second is and all other cumulants disappear.
Characteristic function
The characteristic function for a standard normally distributed random variable is
- .
For a random variable we get :
- .
Moment generating function
The moment-generating function of the normal distribution is
- .
Moments
Let the random variable be -distributed. Then her first moments are as follows:
| order | moment | central moment |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4th | ||
| 5 | ||
| 6th | ||
| 7th | ||
| 8th |
All central moments can be represented by the standard deviation :
the double faculty was used:
A formula for non-central moments can also be specified for. To do this, one transforms and applies the binomial theorem.
Invariance to convolution
The normal distribution is invariant to the convolution , i.e. This means that the sum of independent, normally distributed random variables is normally distributed again (see also under stable distributions and under infinite divisible distributions ). The normal distribution thus forms a convolution half-group in its two parameters. An illustrative formulation of this situation is: The convolution of a Gaussian curve of the half-width with a Gaussian curve FWHM again yields a Gaussian curve with the half-width
- .
So are two independent random variables with
so their sum is also normally distributed:
- .
This can be shown, for example, with the help of characteristic functions by using the fact that the characteristic function of the sum is the product of the characteristic functions of the summands (see the convolution theorem of the Fourier transform).
More generally, independent and normally distributed random variables are given . Then every linear combination is normally distributed again
in particular, the sum of the random variables is normally distributed again
and the arithmetic mean as well
According to Cramér's theorem, the reverse is true: If a normally distributed random variable is the sum of independent random variables, then the summands are also normally distributed.
The density function of the normal distribution is a fixed point of the Fourier transform , i. That is, the Fourier transform of a Gaussian curve is again a Gaussian curve. The product of the standard deviations of these corresponding Gaussian curves is constant; Heisenberg's uncertainty principle applies .
entropy
The normal distribution is the entropy : .
Since it has the greatest entropy of all distributions for a given expected value and a given variance, it is often used as the a priori probability in the maximum entropy method .
Relationships with other distribution functions
Transformation to the standard normal distribution
As mentioned above, a normal distribution with any and and the distribution function has the following relation to the distribution:
- .
Therein is the distribution function of the standard normal distribution.
If so , standardization will lead
to a standard normally distributed random variable , because
- .
From a geometrical perspective, the substitution carried out corresponds to an equal-area transformation of the bell curve from to the bell curve from .
Approximation of the binomial distribution by the normal distribution
The normal distribution can be used to approximate the binomial distribution if the sample size is sufficiently large and the proportion of the property sought is neither too large nor too small in the population ( Moivre-Laplace theorem , central limit theorem , for experimental confirmation see also Galtonbrett ).
If a Bernoulli experiment with mutually independent levels (or random experiments ) is given with a probability of success , the probability of success can generally be calculated by ( binomial distribution ).
This binomial distribution can be approximated by a normal distribution if is sufficiently large and neither too large nor too small. The rule of thumb for this applies . The following then applies to the expected value and the standard deviation :
- and .
This applies to the standard deviation .
If this condition is not met, the inaccuracy of the approximation is still acceptable if: and at the same time .
The following approximation can then be used:
In the normal distribution, the lower limit is reduced by 0.5 and the upper limit is increased by 0.5 to ensure a better approximation. This is also called "continuity correction". It can only be dispensed with if it has a very high value.
Since the binomial distribution is discrete, a few points must be observed:
- The difference between or (and between greater than and greater than or equal to ) must be taken into account (which is not the case with normal distribution). Therefore the next lower natural number has to be chosen, i. H.
- or ,
- so that the normal distribution can be used for further calculations.
- For example:
- Also is
- (necessarily with continuity correction)
- and can thus be calculated using the formula given above.
The great advantage of the approximation is that very many levels of a binomial distribution can be determined very quickly and easily.
Relationship to the Cauchy distribution
The quotient of two stochastically independent -standard normally distributed random variables is Cauchy-distributed .
Relationship to the chi-square distribution
The square of a normally distributed random variable has a chi-square distribution with one degree of freedom . So: if , then . Furthermore, if there are stochastically independent chi-square distributed random variables, then it applies
- .
From this it follows with independent and standard normal distributed random variables :
Other relationships are:
- The sum with and independent normally distributed random variables satisfies a chi-square distribution with degrees of freedom.
- As the number of degrees of freedom increases ( df ≫ 100), the chi-square distribution approaches the normal distribution.
- The chi-square distribution is used to estimate the confidence level for the variance of a normally distributed population.
Relationship to the Rayleigh distribution
The magnitude of two independent normally distributed random variables , each with a mean and the same variances , is Rayleigh distributed with parameters .
Relation to the logarithmic normal distribution
If the random variable normally distributed with , then the random variable is log-normally distributed , ie .
The emergence of a logarithmic normal distribution is due to multiplicative factors, whereas a normal distribution is due to the additive interaction of many random variables.
Relationship to the F-distribution
If the stochastically independent and identically normally distributed random variables and the parameters
own, then the random variable is subject to
an F-distribution with degrees of freedom. Are there
- .
Relationship to Student's t-distribution
If the independent random variables are identically normally distributed with the parameters and , then the continuous random variable is subject to
with the sample mean and the sample variance of a Student's t-distribution with degrees of freedom.
For an increasing number of degrees of freedom, the Student's t-distribution approaches the normal distribution ever closer. As a rule of thumb, from around the Student's t-distribution onwards, if necessary, one can approximate the normal distribution.
Student's t-distribution is used to estimate the confidence for the expected value of a normally distributed random variable with unknown variance.
Calculate with the standard normal distribution
In the case of tasks in which the probability of - normally distributed random variables is to be determined using the standard normal distribution, it is not necessary to calculate the transformation given above every time. Instead, it just does the transformation
used to generate a -distributed random variable .
The probability for the event that e.g. B. lies in the interval , is equal to a probability of the standard normal distribution by the following conversion:
- .
Fundamental questions
In general, the distribution function gives the area under the bell-shaped curve up to the value , i.e. That is, the definite integral of to is calculated.
In tasks, this corresponds to a desired probability in which the random variable is smaller or not larger than a certain number . Because of the continuity of the normal distribution, it makes no difference whether it is now or required, because z. B.
- and thus .
The same applies to “larger” and “not smaller”.
Because it can only be smaller or larger than a limit (or within or outside of two limits), two fundamental questions arise for problems with probability calculations for normal distributions:
- What is the probability that in a random experiment the standard normally distributed random variable takes on at most the value ?
- In school mathematics , the term left pointed is occasionally used for this statement , since the area under the Gaussian curve runs from the left to the border. For negative values are allowed. However, many tables of the standard normal distribution only have positive entries - because of the symmetry of the curve and the rule of negativity
- of the "left tip", this is not a restriction.
- What is the probability that in a random experiment the standard normally distributed random variable takes at least the value ?
- The term right pointed is occasionally used here, with
- there is also a negativity rule here.
Since every random variable with the general normal distribution can be converted into the random variable with the standard normal distribution , the questions apply equally to both quantities.
Scatter area and anti-scatter area
Often the probability is of interest for a range of variation ; H. the probability that the standard normally distributed random variable takes on values between and :
In the special case of the symmetrical scatter range ( , with ) applies
For the corresponding anti-scatter range , the probability that the standard normally distributed random variable assumes values outside the range between and is:
Thus follows with a symmetrical anti-scattering region
Scatter areas using the example of quality assurance
Both ranges are of particular importance. B. in quality assurance of technical or economic production processes . There are tolerance limits to be observed here and , whereby there is usually a greatest still acceptable distance from the expected value (= the optimal target value). The standard deviation , on the other hand, can be obtained empirically from the production process.
If the tolerance interval to be observed was specified, then (depending on the question) there is a symmetrical or anti-scatter area.
In the case of the spread:
- .
The anti-scatter area then results from
or if no spread was calculated by
The result is the probability for sellable products, while the probability means for rejects, both of which are dependent on the specifications of , and .
If it is known that the maximum deviation is symmetrical around the expected value, then questions are also possible in which the probability is given and one of the other variables has to be calculated.
Testing for normal distribution
The following methods and tests can be used to check whether the available data are normally distributed:
- Chi-square test
- Kolmogorov-Smirnov test
- Anderson-Darling test (modification of the Kolmogorow-Smirnow test)
- Lilliefors test (modification of the Kolmogorow-Smirnow test)
- Cramér von Mises test
- Shapiro-Wilk test
- Jarque Bera test
- QQ plot (descriptive review)
- Maximum likelihood method (descriptive check)
The tests have different characteristics in terms of the types of deviations from normal distribution that they detect. The Kolmogorov-Smirnov test recognizes deviations in the middle of the distribution rather than deviations at the edges, while the Jarque-Bera test reacts quite sensitively to strongly deviating individual values at the edges (" heavy edges ").
In contrast to the Kolmogorov-Smirnov test, the Lilliefors test does not have to be standardized; i.e., and the assumed normal distribution may be unknown.
With the help of quantile-quantile diagrams or normal-quantile diagrams, a simple graphic check for normal distribution is possible.
The maximum likelihood method can be used to estimate the parameters and the normal distribution and graphically compare the empirical data with the fitted normal distribution.
Parameter estimation, confidence intervals and tests
Many of the statistical questions in which the normal distribution occurs have been well studied. The most important case is the so-called normal distribution model, which is based on the implementation of independent and normally distributed experiments. There are three cases:
- the expected value is unknown and the variance is known
- the variance is unknown and the expected value is known
- Expected value and variance are unknown.
Depending on which of these cases occurs, different estimation functions , confidence ranges or tests result. These are summarized in detail in the main article normal distribution model.
The following estimation functions are of particular importance:
- The sample mean
- is an unbiased estimator for the unknown expected value for both known and unknown variance. In fact, he is the best unbiased estimator ; H. the estimator with the smallest variance. Both the maximum likelihood method and the moment method provide the sample mean as an estimator.
- The uncorrected sample variance
- .
- is an unbiased estimator for the unknown variance for a given expected value . It can also be obtained both from the maximum likelihood method and from the moment method.
- .
- is an unbiased estimator for the unknown variance when the expected value is unknown.
Generation of normally distributed random numbers
All of the following methods generate random numbers with standard normal distribution. Any normally distributed random numbers can be generated from this by linear transformation: If the random variable is -distributed, then finally -distributed.
Box-Muller method
Using the Box-Muller method , two independent, standard normally distributed random variables and two independent, uniformly distributed random variables , so-called standard random numbers , can be simulated:
and
Polar method
George Marsaglia's Polar method is even faster on a computer because it does not require evaluations of trigonometric functions:
- Generate two independent random numbers, equally distributed in the interval and
- Calculate . If or , go back to step 1.
- Calculate .
- for provides two independent, standard normally distributed random numbers and .
Rule of twelve
The central limit theorem states that under certain conditions the distribution of the sum of independently and identically distributed random numbers approaches a normal distribution.
A special case is the rule of twelve , which is limited to the sum of twelve random numbers from an even distribution on the interval [0,1] and which already leads to acceptable distributions.
However, the required independence of the twelve random variables is not guaranteed for the linear congruence generators (LKG) that are still frequently used . On the contrary, the spectral test for LKG usually only guarantees the independence of a maximum of four to seven of the . The rule of twelve is therefore very questionable for numerical simulations and should, if at all, only be used with more complex but better pseudo-random generators such as B. the Mersenne Twister (standard in Python , GNU R ) or WELL can be used. Other methods, even easier to program, are therefore i. d. R. preferable to the rule of twelve.
Rejection method
Normal distributions can be simulated with the rejection method (see there).
Inversion method
The normal distribution can also be calculated using the inversion method.
Since the error integral cannot be explicitly integrated with elementary functions, one can fall back on series expansion of the inverse function for a starting value and subsequent correction with the Newton method. These are and are needed, which in turn can be calculated with series expansion and continued fraction expansion - overall a relatively high effort. The necessary developments can be found in the literature.
Development of the inverse error integral (can only be used as a starting value for the Newton method because of the pole):
with the coefficients
Applications outside of probability
The normal distribution can also be used to describe not directly stochastic facts, for example in physics for the amplitude profile of the Gaussian rays and other distribution profiles.
It is also used in the Gabor transformation .
See also
literature
- Stephen M. Stigler: The history of statistics: the measurement of uncertainty before 1900. Belknap Series. Harvard University Press, 1986. ISBN 9780674403413 .
Web links
- Clear explanation of the normal distribution with an interactive graph
- Representation with program code ( Memento from February 7, 2018 in the Internet Archive ) in Visual Basic Classic
- Online calculator normal distribution
Individual evidence
- ↑ Wolfgang Götze, Christel Deutschmann, Heike Link: Statistics. Text and exercise book with examples from the tourism and transport industry . Oldenburg, Munich 2002, ISBN 3-486-27233-0 , p. 170 ( limited preview in Google Book search).
- ↑ Hans Wußing: From Gauß to Poincaré: Mathematics and the industrial revolution. P. 33.
- ↑ This is the exponential function with the base
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee: Introduction to the Theory and Practice of Econometrics. 1988, p. 47.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee: Introduction to the Theory and Practice of Econometrics. 1988, p. 48.
- ^ H. Schmid, A. Huber: Measuring a Small Number of Samples and the 3σ Fallacy. (PDF) In: IEEE Solid-State Circuits Magazine. Vol. 6, No. 2, 2014, pp. 52-58, doi : 10.1109 / MSSC.2014.2313714 .
- ↑ Mareke Arends: Epidemiology of bulimic symptoms among 10-grade students in the city of Halle. Dissertation. Martin Luther University of Halle-Wittenberg, 2005 Table 9, p 30 urn : nbn: de: gbv: 3-000008151
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee: Introduction to the Theory and Practice of Econometrics. 1988, p. 49.
- ^ William B. Jones, WJ Thron: Continued Fractions: Analytic Theory and Applications. Addison-Wesley, 1980.








































































































![[\ mu -z \ sigma; \ mu + z \ sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2853d29534da7711f5c3f5b91adcebc26ab18c3)




























































































![[x, y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)




















![{\ displaystyle [x_ {1}; x_ {2}] = [\ mu - \ epsilon; \ mu + \ epsilon]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6722a4fa0e23c0a1461b65d075ac5d47fb9bab7e)

















![[-1, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)














