Bernoulli distribution
Random variables with a Bernoulli distribution (also referred to as zero-one distribution , alternative distribution or Boole distribution ) are used to describe random events for which there are only two possible test outcomes. One of the test results is usually referred to as success and the complementary test result as failure . The associated probability of success is called the probability of success and the probability of failure. Examples:
- Flipping a coin : head (success) , and number (failure) .
- Throwing a die, only a “6” counting as a success: , .
- Quality inspection (perfect, not perfect).
- System check (works, doesn't work).
- Consider a very small space / time interval: event occurs , does not occur .
The term Bernoulli trial ( Bernoullian trials after Jakob I Bernoulli ) was first used in 1937 in the book Introduction to Mathematical Probability by James Victor Uspensky .
definition
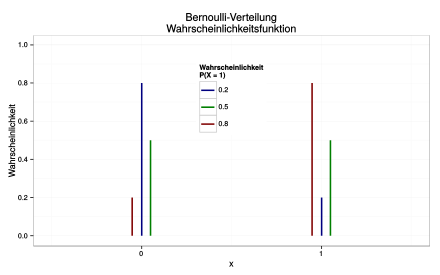
A discrete random variable with values in the set is subject to the zero-one distribution or Bernoulli distribution with the parameter if it follows the following probability function
- .
The distribution function is then
- .
Then you write or .
A series of independent, identical experiments, in which each individual experiment satisfies the Bernoulli distribution, is called the Bernoulli process or Bernoulli experiment scheme.
properties
Expected value
The Bernoulli distribution with parameters has the expected value :
The reason for this is that for a Bernoulli-distributed random variable with and the following applies:
Variance and other measures of dispersion
The Bernoulli distribution has the variance
because it is and with it
- .
So that is the standard deviation
and the coefficient of variation
- .
symmetry
For the parameter , the Bernoulli distribution is symmetrical about the point .
Crookedness
The skewness of the Bernoulli distribution is
- .
This can be shown as follows. A standardized random variable with Bernoulli distribution assumes the value with probability and the value with probability . So we get for the skew
Bulge and excess
The excess of the Bernoulli distribution is
and with that is the bulge
- .
Moments
All kth moments are the same and it holds
- .
Because it is
- .
entropy
The entropy of the Bernoulli distribution is
measured in bits .
mode
The mode of the Bernoulli distribution is
- .
Median
The median of the Bernoulli distribution is
if true, each is a median.
Accumulators
The cumulative generating function is
- .
Therewith the first cumulants are and the recursion equation applies
Probability generating function
The probability generating function is
- .
Characteristic function
The characteristic function is
- .
Moment generating function
The moment generating function is
- .
Relationship to other distributions
Relationship to the binomial distribution
The Bernoulli distribution is a special case of the binomial distribution for . In other words, the sum of independent Bernoulli-distributed random variables with identical parameters satisfies the binomial distribution, so the Bernoulli distribution is not reproductive . The binomial distribution is the -fold convolution of the Bernoulli distribution with the same parameters or with equal probability .
Relationship to the generalized binomial distribution
The sum of mutually independent Bernoulli-distributed random variables, which all have a different parameter , is generally binomially distributed .
Relationship to the Poisson distribution
The sum of Bernoulli-distributed random quantities is sufficient for , and a Poisson distribution with the parameter . This follows directly from the fact that the sum is binomially distributed and the Poisson approximation applies to the binomial distribution .
Relationship to the two-point distribution
The Bernoulli distribution is a special case of the two-point distribution with . Conversely, the two-point distribution is a generalization of the Bernoulli distribution to any two-element point sets.
Relationship to the Rademacher distribution
Both the Bernoulli distribution with and the Rademacher distribution model a fair coin toss (or a fair, random yes / no decision). The only difference is that heads (success) and tails (failure) are coded differently.
Relationship to the geometric distribution
When performing Bernoulli-distributed experiments one after the other, the waiting time for the first success (or last failure, depending on the definition) is geometrically distributed .
Relationship to discrete equal distribution
The Bernoulli distribution with is a discrete uniform distribution on .
Urn model
The Bernoulli distribution can also be generated from the urn model if is. Then this corresponds to the one-time pulling out of an urn with balls, of which exactly are red and all others have a different color. The probability of drawing a red ball is then Bernoulli-distributed.
simulation
The simulation makes use of the fact that if a continuously uniformly distributed random variable is on , the random variable is Bernoulli-distributed with parameters . Since almost any computer can generate standard random numbers, the simulation is as follows:
- Generate a standard random number
- Is , print 0, otherwise print 1.
This corresponds exactly to the inversion method . The simple simulability of Bernoulli-distributed random variables can also be used to simulate binomial distributed or generalized binomial distributed random variables.
literature
- Hans-Otto Georgii: Stochastics: Introduction to probability theory and statistics. 4th edition, de Gruyter, 2009, ISBN 978-3-11-021526-7 .
Individual evidence
- ↑ Norbert Kusolitsch: Measure and probability theory . An introduction. 2nd, revised and expanded edition. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1 , p. 63 , doi : 10.1007 / 978-3-642-45387-8 .
- ↑ Klaus D. Schmidt: Measure and probability . 2nd, revised edition. Springer-Verlag, Heidelberg Dordrecht London New York 2011, ISBN 978-3-642-21025-9 , pp. 254 , doi : 10.1007 / 978-3-642-21026-6 .
- ↑ James Victor Uspensky: Introduction to Mathematical Probability , McGraw-Hill, New York 1937, p. 45













![p \ in [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)




















![{\ displaystyle {\ begin {aligned} \ operatorname {v} (X) & = \ operatorname {E} \ left [\ left ({\ frac {X- \ operatorname {E} (X)} {\ sqrt {\ operatorname {Var} (X)}}} \ right) ^ {3} \ right] \\ & = p \ cdot \ left ({\ frac {q} {\ sqrt {pq}}} \ right) ^ {3 } + q \ cdot \ left (- {\ frac {p} {\ sqrt {pq}}} \ right) ^ {3} \\ & = {\ frac {1} {{\ sqrt {pq}} ^ { 3}}} \ left (pq ^ {3} -qp ^ {3} \ right) \\ & = {\ frac {pq} {{\ sqrt {pq}} ^ {3}}} (qp) \\ & = {\ frac {qp} {\ sqrt {pq}}} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/444b272655aba54f608ed51507bd0de15adec89c)









![{\ displaystyle {\ tilde {m}} _ {X} \ in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9fd9d909c8c8833e0a4a7b1380b09a8ff318c5)




















![[0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


