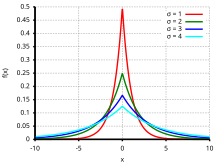
Density functions of the Laplace distribution for different parameters
The Laplace distribution (named after Pierre-Simon Laplace , a French mathematician and astronomer) is a continuous probability distribution . Since it has the form of two exponential distributions joined together , it is also known as the double exponential distribution or two-sided exponential distribution .
definition A continuous random variable is subject to the Laplace distribution with the location parameter and the scale parameter if it has the probability density
X
{\ displaystyle X}
μ
∈
R.
{\ displaystyle \ mu \ in \ mathbb {R}}
σ
>
0
{\ displaystyle \ sigma> 0}
f
(
x
)
=
1
2
σ
e
-
|
x
-
μ
|
σ
{\ displaystyle f (x) = {\ frac {1} {2 \ sigma}} e ^ {\ displaystyle - {\ frac {\ left | x- \ mu \ right |} {\ sigma}}}}
owns.
Its distribution function is
F.
(
x
)
=
{
1
2
e
x
-
μ
σ
,
x
≤
μ
1
-
1
2
e
-
x
-
μ
σ
x
>
μ
{\ displaystyle F (x) = {\ begin {cases} \ displaystyle {1 \ over 2} e ^ {\ displaystyle {\ frac {x- \ mu} {\ sigma}}}, & x \ leq \ mu \\ \ displaystyle 1- {1 \ over 2} e ^ {\ displaystyle - {\ frac {x- \ mu} {\ sigma}}} & x> \ mu \ end {cases}}}
Using the Signum function , it can be displayed as closed
F.
(
x
)
=
1
2
+
1
2
so-called
(
x
-
μ
)
(
1
-
exp
(
-
|
x
-
μ
|
σ
)
)
{\ displaystyle F (x) = {\ tfrac {1} {2}} + {\ tfrac {1} {2}} \ operatorname {sgn} \ left (x- \ mu \ right) \ left (1- \ exp \ left (- {\ frac {\ left | x- \ mu \ right |} {\ sigma}} \ right) \ right)}
properties symmetry The probability density is axisymmetric to the straight line and the distribution function is point-symmetric to the point .
x
=
μ
{\ displaystyle x = \ mu}
(
μ
,
1
/
2
)
{\ displaystyle (\ mu, 1/2)}
Expected value, median, mode value
The parameter is expected value , median and mode value at the same time .
μ
{\ displaystyle \ mu}
E.
(
X
)
=
μ
{\ displaystyle \ operatorname {E} (X) = \ mu}
Variance The variance is determined by the parameter .
σ
{\ displaystyle \ sigma}
Var
(
X
)
=
2
σ
2
{\ displaystyle \ operatorname {Var} (X) = 2 \ sigma ^ {2}}
Crookedness The skewness of the Laplace distribution is
v
(
X
)
=
0
{\ displaystyle \ operatorname {v} (X) = 0}
Kurtosis The curvature of a Laplace distribution is identical to 6 (corresponds to an excess of 3).
Kurt
(
X
)
=
6th
{\ displaystyle \ operatorname {Kurt} (X) = 6}
Accumulators All cumulants with an odd degree are zero. For straight applies
κ
k
{\ displaystyle \ kappa _ {k}}
k
>
2
{\ displaystyle k> 2}
k
{\ displaystyle k}
κ
k
=
2
(
k
-
1
)
!
σ
k
{\ displaystyle \ kappa _ {k} = 2 (k-1)! \ sigma ^ {k}}
Moment generating function The moment-generating function is a Laplace-distributed random variable with parameters and is
μ
{\ displaystyle \ mu}
σ
{\ displaystyle \ sigma}
M.
X
(
t
)
=
e
μ
t
1
-
σ
2
t
2
{\ displaystyle M_ {X} (t) = {\ frac {e ^ {\ mu t}} {1- \ sigma ^ {2} t ^ {2}}}}
|
t
|
<
1
/
σ
.
{\ displaystyle | t | <1 / \ sigma.}
Characteristic function The characteristic function arises from the moment-generating function by replacing the argument with , one obtains:
t
{\ displaystyle t}
i
s
{\ displaystyle is}
ϕ
X
(
s
)
=
e
i
μ
s
1
+
σ
2
s
2
{\ displaystyle \ phi _ {X} (s) = {\ frac {e ^ {i \ mu s}} {1+ \ sigma ^ {2} s ^ {2}}}}
entropy The entropy of the Laplace distribution (expressed in nats ) is
1
+
ln
(
2
σ
)
{\ displaystyle 1+ \ ln (2 \ sigma)}
Random numbers The inversion method is suitable for generating random numbers with double exponential distribution .
The pseudo inverse of the distribution function to be formed according to the simulation lemma reads here
F.
-
1
(
y
)
=
{
1
λ
ln
(
2
y
)
y
<
1
2
-
1
λ
ln
(
2
(
1
-
y
)
)
,
y
≥
1
2
{\ displaystyle F ^ {- 1} (y) = {\ begin {cases} \ displaystyle {1 \ over \ lambda} \ ln (2y) & y <{1 \ over 2} \\\ displaystyle - {1 \ over \ lambda} \ ln (2 (1-y)), & y \ geq {1 \ over 2} \ end {cases}}}
A sequence can therefore be added to a sequence of standard random numbers
u
i
{\ displaystyle u_ {i}}
x
i
: =
F.
-
1
(
u
i
)
{\ displaystyle x_ {i}: = F ^ {- 1} (u_ {i})}
Calculate double exponentially distributed random numbers .
Relationship to other distributions Relationship to normal distribution If independent standard normal distributions are random variables, then standard laplace is distributed ( ).
X
1
,
X
2
,
X
3
,
X
4th
∼
N
(
0
,
1
)
{\ displaystyle X_ {1}, X_ {2}, X_ {3}, X_ {4} \ sim {\ mathcal {N}} (0,1)}
Z
=
det
(
X
1
X
2
X
3
X
4th
)
=
X
1
X
4th
-
X
2
X
3
{\ displaystyle Z = \ det {\ begin {pmatrix} X_ {1} & X_ {2} \\ X_ {3} & X_ {4} \ end {pmatrix}} = X_ {1} \, X_ {4} -X_ {2} \, X_ {3}}
μ
=
0
{\ displaystyle \ mu = 0}
Relationship to the exponential distribution A random variable , which is defined as the difference between two independent exponentially distributed random variables and with the same parameter, is Laplace distributed.
X
: =
Y
λ
-
Z
λ
{\ displaystyle X: = Y _ {\ lambda} -Z _ {\ lambda}}
Y
λ
{\ displaystyle Y _ {\ lambda}}
Z
λ
{\ displaystyle Z _ {\ lambda}}
Relationship to the Rademacher distribution If Rademacher is distributed and exponentially distributed to the parameter , then Laplace distributed to the position parameter is 0 and the scale parameter .
X
{\ displaystyle X}
Y
{\ displaystyle Y}
λ
{\ displaystyle \ lambda}
X
⋅
Y
{\ displaystyle X \ cdot Y}
1
λ
{\ displaystyle {\ frac {1} {\ lambda}}}
Demarcation from constant uniform distribution The continuous Laplace distribution defined in this way has nothing to do with the continuous uniform distribution . It is still often confused with it because the discrete uniform distribution is named after Laplace ( Laplace cube ).
Web links swell
^ Georgii: Stochastics. 2009, p. 225.
↑ Milton Abramowitz and Irene Stegun : Handbook of Mathematical Functions
Discrete univariate distributions
Continuous univariate distributions
Multivariate distributions
<img src="https://de.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">