Characteristic function (stochastics)

In probability theory, a characteristic function is a special complex-valued function that is assigned to a finite measure or, more specifically, a probability measure on the real numbers or the distribution of a random variable . The finite measure is clearly determined by its characteristic function and vice versa, so the assignment is bijective .

An essential benefit of characteristic functions is that many more difficult to grasp properties of the finite measure are found as properties of the characteristic function and are there more easily accessible as properties of a function. For example, the convolution of probability measures is reduced to the multiplication of the corresponding characteristic functions.

definition

A finite measure is given . Then the name is the complex-valued function ${\displaystyle \mu }$ ${\displaystyle (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))}$

${\displaystyle \varphi _{\mu }\colon \mathbb {R} \to \mathbb {C} }$

defined by

${\displaystyle \varphi _{\mu }(t):=\int _{\mathbb {R} }\exp(\mathrm {i} tx)\,\mu (\mathrm {d} x)}$

the characteristic function of . If a probability measure , the definition follows analogously. If a random variable with distribution is given, the characteristic function is given by ${\displaystyle \mu }$ ${\displaystyle \mu =P}$ ${\displaystyle X}$ ${\displaystyle P_{X}}$

${\displaystyle \varphi _{X}(t)=\operatorname {E} (\exp(\mathrm {i} tX))}$

with the expected value . ${\displaystyle \operatorname {E} }$

This results in the following important special cases:

• If has a probability density function (with respect to the Riemann integral) , then the characteristic function is given as ${\displaystyle P_{X}}$ ${\displaystyle f_{X}(x)}$

${\displaystyle \varphi _{X}(t)=\int _{-\infty }^{\infty }f_{X}(x)\exp(\mathrm {i} tx)\,\mathrm {d} x}$.

• If has a probability function , then the characteristic function is given as ${\displaystyle P_{X}}$ ${\displaystyle p_{X}}$

${\displaystyle \varphi _{X}(t)=\sum _{k=1}^{\infty }\exp(\mathrm {i} tx_{k})p_{X}(x_{k})}$.

In both cases, the characteristic function is the (continuous or discrete) Fourier transform of the density or probability function.

Elementary examples

If Poisson is distributed , then has the probability function ${\displaystyle X}$ ${\displaystyle P_{X}}$

${\displaystyle p_{\lambda }(k)={\frac {\lambda ^{k}}{k!}}\,\mathrm {e} ^{-\lambda }\quad {\text{für}}\quad k\in \mathbb {N} }$.

The above representation for the characteristic function using probability functions then results

${\displaystyle \varphi _{X}(t)=\sum _{k=0}^{\infty }\exp(\mathrm {i} tk){\frac {\lambda ^{k}}{k!}}\,\mathrm {e} ^{-\lambda }=\mathrm {e} ^{-\lambda }\sum _{k=0}^{\infty }{\frac {\left(\lambda e^{it}\right)^{k}}{k!}}=\mathrm {e} ^{\lambda (e^{it}-1)}}$

If it is exponentially distributed to the parameter , then has the probability density function ${\displaystyle Y}$ ${\displaystyle \lambda }$ ${\displaystyle P_{Y}}$

${\displaystyle f_{\lambda }(x)={\begin{cases}\displaystyle \lambda \mathrm {e} ^{-\lambda x}&x\geq 0\\0&x<0\end{cases}}}$

This results in

${\displaystyle \varphi _{Y}(t)=\int _{0}^{\infty }e^{\mathrm {i} tx}\lambda \mathrm {e} ^{-\lambda x}\mathrm {d} x=\lambda \int _{0}^{\infty }e^{x(\mathrm {i} t-\lambda )}\mathrm {d} x={\frac {\lambda }{\lambda -\mathrm {i} t}}}$

Further examples of characteristic functions are tabulated further down in the article or can be found directly in the article about the corresponding probability distributions.

Properties as a function

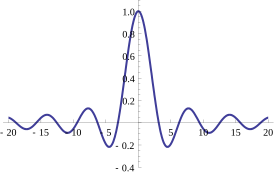
The characteristic function of a random variable that is continuously uniformly distributed over (-1,1). In general, however, characteristic functions are not real-valued.

existence

The characteristic function exists for any finite measures and thus also probability measures or distributions of random variables, because

${\displaystyle \left|e^{\mathrm {i} tx}\right|=1}$

the integral always exists.

Narrow-mindedness

Every characteristic function is always limited; for a random variable , that ${\displaystyle X}$

${\displaystyle \left|\varphi _{X}(t)\right|\leq \varphi _{X}(0)=1}$.

In the general case of a finite measure on holds ${\displaystyle \mu }$ ${\displaystyle (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))}$

${\displaystyle \left|\varphi _{\mu }(t)\right|\leq \varphi _{\mu }(0)=\mu (\mathbb {R} )}$.

symmetry

The characteristic function is real-valued if and only if the random variable is symmetric . ${\displaystyle \varphi _{X}}$ ${\displaystyle X}$

Furthermore , it is always Hermitian, that is, it applies ${\displaystyle \varphi _{X}}$

${\displaystyle \varphi _{X}(-t)={\overline {\varphi _{X}(t)}}}$.

Uniform continuity

${\displaystyle \varphi _{X}}$is a uniformly continuous function.

characterization

It is particularly interesting when a function is the characteristic function of a probability measure. Pólya's theorem (after George Pólya ) provides a sufficient condition : It is a function ${\displaystyle f\colon \mathbb {R} \to \mathbb {C} }$

${\displaystyle f\colon \mathbb {R} \to [0,1]}$

• convex on as well ${\displaystyle [0,\infty )}$
• steady and straight

and, in addition , it is the characteristic function of a probability measure. ${\displaystyle f(0)=1}$

Bochner's theorem (after Salomon Bochner ) provides a necessary and sufficient condition :

A continuous function

${\displaystyle f\colon \mathbb {R} \to \mathbb {C} }$

is the characteristic function of a probability measure if and only if a positive semidefinite function is and holds. ${\displaystyle f}$ ${\displaystyle f(0)=1}$

Other properties

Linear transformation

${\displaystyle \varphi _{aX+b}(t)=e^{\mathrm {i} tb}\varphi _{X}(at)}$   for all ${\displaystyle a,b\in \mathbb {R} \,.}$

Reversibility

If integrable , then the probability density of can be reconstructed as ${\displaystyle \varphi _{X}}$ ${\displaystyle X}$

${\displaystyle f_{X}(x)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }e^{-\mathrm {i} tx}\varphi _{X}(t)\,\mathrm {d} t\,.}$

Moment generation

${\displaystyle \operatorname {E} (X^{k})={\frac {\varphi _{X}^{(k)}(0)}{\mathrm {i} ^{k}}}}$   for all natural , if . ${\displaystyle k\in \mathbb {N} }$ ${\displaystyle \operatorname {E} (|X|^{k})<\infty }$

In particular, the special cases arise

${\displaystyle \operatorname {E} (X)={\frac {\varphi _{X}'(0)}{\mathrm {i} }}\,,}$

${\displaystyle \operatorname {E} (X^{2})=-\varphi _{X}''(0)\,.}$

If the expectation value is finite for a natural number , then -mal is continuously differentiable and can be expanded into a Taylor series um : ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle \operatorname {E} (|X|^{n})}$ ${\displaystyle \varphi _{X}}$ ${\displaystyle n}$ ${\displaystyle 0}$

${\displaystyle \varphi _{X}(t)=\sum \limits _{k=0}^{n}{\frac {\varphi _{X}^{(k)}(0)}{k!}}t^{k}+R_{n+1}(t)=\sum \limits _{k=0}^{n}{\frac {(\mathrm {i} t)^{k}}{k!}}\operatorname {E} (X^{k})+R_{n+1}(t)\,.}$

An important special case is the development of a random variable with and : ${\displaystyle X}$ ${\displaystyle \operatorname {E} (X)=0}$ ${\displaystyle \operatorname {Var} (X)=1}$

${\displaystyle \varphi _{X}(t)=1-{\frac {1}{2}}t^{2}+R_{3}(t)\quad {\text{mit}}\quad \lim \limits _{t\rightarrow 0}{\frac {R_{3}(t)}{t^{2}}}=0\,.}$

Convolution formula for densities

For independent random variables and applies to the characteristic function of the sum ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$ ${\displaystyle Y=X_{1}+X_{2}}$

${\displaystyle \varphi _{Y}(t)=\varphi _{X_{1}}(t)\,\varphi _{X_{2}}(t)\,,}$

because because of independence applies

${\displaystyle \varphi _{Y}(t)=\operatorname {E} \left(e^{\mathrm {i} t(X_{1}+X_{2})}\right)=\operatorname {E} \left(e^{\mathrm {i} tX_{1}}e^{\mathrm {i} tX_{2}}\right)=\operatorname {E} \left(e^{\mathrm {i} tX_{1}}\right)\operatorname {E} \left(e^{\mathrm {i} tX_{2}}\right)=\varphi _{X_{1}}(t)\,\varphi _{X_{2}}(t)\,.}$

Characteristic function of random sums

If independently identically distributed random variables and a -value random variable that is independent of all , then the characteristic function of the random variable can be ${\displaystyle (X_{i})_{i\in \mathbb {N} }}$ ${\displaystyle N}$ ${\displaystyle \mathbb {N} _{0}}$ ${\displaystyle X_{i}}$

${\displaystyle S:=\sum _{i=1}^{N}X_{i}}$

as a concatenation of the probability-generating function of and the characteristic function of : ${\displaystyle m_{N}(t)}$ ${\displaystyle N}$ ${\displaystyle X_{1}}$

${\displaystyle \varphi _{S}(t)=m_{N}(\varphi _{X_{1}}(t))}$.

Uniqueness set

The following theorem of uniqueness applies: If , are random variables and holds for all , then , i. H. and have the same distribution function. Hence, it can easily be used to determine the convolution of some distributions. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \varphi _{X}(t)=\varphi _{Y}(t)}$ ${\displaystyle t\in \mathbb {R} }$ ${\displaystyle X{\overset {d}{=}}Y}$ ${\displaystyle X}$ ${\displaystyle Y}$

From the uniqueness theorem, Lévy's continuity theorem can be deduced: If is a sequence of random variables, then ( convergence in distribution ) holds if and only if holds for all . This property can be used with central limit value sets. ${\displaystyle (X_{n})_{n\in \mathbb {N} }}$ ${\displaystyle X_{n}{\stackrel {d}{\rightarrow }}X}$ ${\displaystyle \lim \limits _{n\rightarrow \infty }\varphi _{X_{n}}(t)=\varphi _{X}(t)}$ ${\displaystyle t\in \mathbb {R} }$

Examples

distribution	Characteristic function ${\displaystyle \varphi _{X}(t)}$
Discrete distributions
Binomial distribution ${\displaystyle X\sim \operatorname {Bin} (n,p)}$	${\displaystyle \varphi _{X}(t)=\left(pe^{\mathrm {i} t}+1-p\right)^{n}}$
Poisson distribution ${\displaystyle X\sim \operatorname {Poi} (\lambda )}$	${\displaystyle \varphi _{X}(t)=e^{\lambda \left(e^{\mathrm {i} t}-1\right)}}$
Negative binomial distribution ${\displaystyle X\sim \operatorname {NegBin} (r,p)}$	${\displaystyle \varphi _{X}(t)=\left({\frac {1-pe^{\mathrm {i} t}}{1-p}}\right)^{-r}}$
Absolutely continuous distributions
${\displaystyle X\sim N(0,1)}$ standard normally distributed	${\displaystyle \varphi _{X}(t)=e^{-{\frac {t^{2}}{2}}}}$
${\displaystyle X\sim N(\mu ,\sigma ^{2})}$ normally distributed	${\displaystyle \varphi _{X}(t)=e^{\mathrm {i} t\mu }e^{-{\frac {\sigma ^{2}t^{2}}{2}}}}$
${\displaystyle X\sim U(a,b)}$ evenly distributed	${\displaystyle \varphi _{X}(t)={\frac {e^{\mathrm {i} bt}-e^{\mathrm {i} at}}{\mathrm {i} (b-a)t}}}$
${\displaystyle X\sim \;C(0,1)}$ Standard Cauchy distributed	${\displaystyle \varphi _{X}(t)=e^{-|t|}}$
${\displaystyle X\sim \;G(p,b)}$ gamma distributed	${\displaystyle \varphi _{X}(t)=\left({\frac {b}{b-\mathrm {i} t}}\right)^{p}}$

More general definitions

Definition of multidimensional random variables

The characteristic function can be extended to -dimensional real random vectors as follows: ${\displaystyle \ell }$ ${\displaystyle \mathbf {X} =(X_{1},\dotsc ,X_{\ell })}$

${\displaystyle \varphi _{\mathbf {X} }(t)=\varphi _{\mathbf {X} }(t_{1},\dots ,t_{l})=\operatorname {E} (e^{i\langle t,\mathbf {X} \rangle })=\operatorname {E} \left(\prod _{j=1}^{\ell }e^{it_{j}X_{j}}\right)}$,

where denotes the standard scalar product. ${\displaystyle \langle t,\mathbf {X} \rangle =\sum \limits _{j=1}^{\ell }t_{j}X_{j}}$

Definition of nuclear space

The concept of characteristic function also exists for nuclear spaces . The function , defined in the nuclear space , is called characteristic function if the following properties apply: ${\displaystyle \varphi :N\rightarrow \mathbb {C} }$ ${\displaystyle N}$

• ${\displaystyle \varphi }$ is steady
• ${\displaystyle \varphi }$is positive definite, i.e. H. for each choice is ${\displaystyle \alpha _{1},\ldots ,\alpha _{n}\in \mathbb {C} ,\xi _{1},\ldots ,\xi _{n}\in N,}$

${\displaystyle \sum _{j,k=1}^{n}\alpha _{j}{\overline {\alpha _{k}}}\varphi (\xi _{j}-\xi _{k})\geq 0,}$

• ${\displaystyle \varphi }$is normalized, i.e. H. ${\displaystyle \varphi (0)=1.}$

In this case, the Bochner-Minlos theorem says that a probability measure is induced on the topological dual space . ${\displaystyle \varphi }$ ${\displaystyle N^{\prime }}$

For random measurements

The characteristic function can also be defined for random dimensions . However, it is then a functional , so its arguments are functions. If a measure is accidental, the characteristic function is given as ${\displaystyle X}$

${\displaystyle \varphi _{X}(f)=\operatorname {E} \left(\exp \left(i\int f\mathrm {d} X\right)\right)}$

for all limited, measurable real-valued functions with compact support . The random measure is clearly determined by the values ​​of the characteristic function on all positive continuous functions with compact support . ${\displaystyle f}$

Relationship to other generating functions

In addition to the characteristic functions, the probability-generating functions and the moment-generating functions also play an important role in probability theory.

The probability-generating function of a -valent random variable is defined as . Accordingly, the relationship applies . ${\displaystyle \mathbb {N} _{0}}$ ${\displaystyle X}$ ${\displaystyle m_{X}(t)=\operatorname {E} (t^{X})}$ ${\displaystyle m_{X}(e^{it})=\varphi _{X}(t)}$

The moment generating function of a random variable is defined as . Accordingly, the relationship applies if the torque-generating function exists. In contrast to the characteristic function, this is not always the case. ${\displaystyle M_{X}(t):=\operatorname {E} (e^{tX})}$ ${\displaystyle M_{iX}(t)=M_{X}(it)=\varphi _{X}(t)}$

There is also the cumulative-generating function as the logarithm of the torque-generating function. The term cumulative is derived from it.

Individual evidence

1. ↑ Achim Klenke: Probability Theory . 3. Edition. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6 , p. 553 , doi : 10.1007 / 978-3-642-36018-3 .

literature

• Eugene Lukacs : Characteristic functions. Griffin, London 1960. 2nd, expanded edition 1970, ISBN 0-85264-170-2
• Achim Klenke: Probability Theory. 2nd Edition. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76317-8

Web links

• NN Vakhania: Characteristic function . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Todd Rowland: Characteristic Function . In: MathWorld (English).