Exponential distribution

Density of the exponential distribution with different values ​​for λ

The exponential distribution (also negative exponential distribution ) is a continuous probability distribution over the set of non-negative real numbers , which is given by an exponential function . It is primarily used as a model when answering the question about the duration of random time intervals , e.g. B.

• Time between two calls
• Lifetime of atoms in radioactive decay
• Service life of components, machines and devices, if signs of aging do not have to be considered.
• as a rough model for small and medium-sized damage in household effects, motor vehicle liability, comprehensive insurance in actuarial mathematics

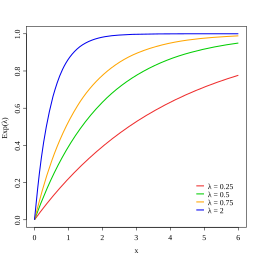
${\displaystyle \lambda }$stands for the number of expected events per unit interval. As can be seen from the diagram, shorter intervals between events (interval length ) are more likely. However, very long intervals also occur less frequently. The probability density can definitely take on values> 1 (e.g. for ), since the area under the curve is normalized to 1 (normalization property). Concrete probability information about the occurrence of the next event can best be obtained from the distribution function . ${\displaystyle x}$ ${\displaystyle \lambda =2}$

Often the actual distribution is not an exponential distribution, but the exponential distribution is easy to handle and is assumed for the sake of simplicity. It is applicable if a Poisson process is present, i.e. the Poisson assumptions are fulfilled.

The exponential distribution is part of the much larger and more general exponential family , a class of probability measures that are easy to use.

definition

A continuous random variable satisfies the exponential distribution with the positive real inverse scale parameter if it is the density function ${\displaystyle X}$ ${\displaystyle \operatorname {Exp} (\lambda )}$ ${\displaystyle \lambda \in \mathbb {R} _{>0}}$

${\displaystyle f_{\lambda }(x)={\begin{cases}\displaystyle \lambda {\rm {e}}^{-\lambda x}&x\geq 0\\0&x<0\end{cases}}}$

owns. If a random variable has this density, then one also writes or . ${\displaystyle X\sim {\mathcal {E}}(\lambda )}$ ${\displaystyle X\sim \operatorname {Exp} (\lambda )}$

The parameter has the character of an event rate and that of an event distance (average range or average service life). ${\displaystyle \lambda }$ ${\displaystyle 1/\lambda }$

An alternative parameterization (especially common in the Anglo-Saxon region) leads to the density function

${\displaystyle f_{\mu }(x)={\begin{cases}\displaystyle {\frac {1}{\mu }}\mathrm {e} ^{-{\frac {x}{\mu }}}&x\geq 0\\0&x<0\end{cases}}}$.

The relationship to the above parameterization is simple . To avoid misunderstandings, it is recommended to state the expected value explicitly, i.e. to speak of an exponential distribution with expected value . ${\displaystyle \mu =1/\lambda }$ ${\displaystyle 1/\lambda }$

properties

Distribution function

Distribution function of the exponential distribution with different values ​​for . ${\displaystyle \lambda }$

The (cumulative) distribution function of the exponential distribution is

${\displaystyle F(x)=\int \limits _{0}^{x}f_{\lambda }\left(t\right)\ {\rm {d}}t={\begin{cases}1-\mathrm {e} ^{-\lambda x}&,x\geq 0\\0&,x<0\end{cases}}}$.

It allows the calculation of the probability of the occurrence of the next event in the interval from to . ${\displaystyle 0}$ ${\displaystyle x}$

The probability of an interval length being greater than that of the next event . ${\displaystyle x}$ ${\displaystyle \mathrm {e} ^{-\lambda x}}$

Expected value

The exponential distribution has the expectation , because ${\displaystyle {\tfrac {1}{\lambda }}}$

${\displaystyle \operatorname {E} (X)=\int \limits _{0}^{\infty }\lambda x\mathrm {e} ^{-\lambda x}\,\mathrm {d} x={\frac {1}{\lambda }}}$.

The expected value corresponds to the average service life of components, machines and devices if signs of aging do not have to be considered. In this context it is referred to as Mean Time Between Failures (MTBF).

Median

The exponential distribution has its median at

${\displaystyle {\tilde {x}}={\frac {\ln 2}{\lambda }}\approx {\frac {0{,}693}{\lambda }}}$.

mode

The density function of the exponential distribution assumes the maximum value at, i.e. i.e., the mode is ${\displaystyle x=0}$

${\displaystyle x_{D}=0}$.

Variance

The variance results analogously using

${\displaystyle \operatorname {Var} (X)=\int \limits _{0}^{\infty }\left(x-{\frac {1}{\lambda }}\right)^{2}\lambda \mathrm {e} ^{-\lambda x}\,\mathrm {d} x=\lambda \int \limits _{0}^{\infty }x^{2}\mathrm {e} ^{-\lambda x}\,\mathrm {d} x-2\int \limits _{0}^{\infty }x\mathrm {e} ^{-\lambda x}\,\mathrm {d} x+{\frac {1}{\lambda }}\int \limits _{0}^{\infty }\mathrm {e} ^{-\lambda x}\,\mathrm {d} x={\frac {1}{\lambda ^{2}}}}$.

Standard deviation

For the standard deviation results

${\displaystyle \sigma ={\sqrt {\operatorname {Var} (X)}}={\sqrt {\frac {1}{\lambda ^{2}}}}={\frac {1}{\lambda }}}$.

Coefficient of variation

The coefficient of variation is obtained directly from the expected value and the variance . It applies

${\displaystyle \operatorname {VarK} (X)={\frac {\sqrt {\sigma ^{2}(X)}}{\operatorname {E} (X)}}={\frac {\sqrt {\operatorname {Var} (X)}}{\operatorname {E} (X)}}}$.

So it applies

${\displaystyle \operatorname {VarK} (X)=1}$.

Geometric mean

The geometric mean of the exponential distribution is

${\displaystyle \operatorname {GM} (X)=\exp \left(\int \limits _{0}^{\infty }\ln(x)\lambda \mathrm {e} ^{-\lambda x}\,\mathrm {d} x\right)=\exp \left(\ln \left({\frac {1}{\lambda }}\right)-\gamma \right)={\frac {1}{\lambda \mathrm {e} ^{\gamma }}}}$,

where denotes the Euler-Mascheroni constant . ${\displaystyle \gamma }$

More spread

The mean absolute deviation

${\displaystyle e={\frac {2/\mathrm {e} }{\lambda }}\approx {\frac {0{,}736}{\lambda }}}$

is smaller than the standard deviation, the mean absolute deviation with respect to the median

${\displaystyle {\mathit {MD}}={\frac {\ln 2}{\lambda }}\approx {\frac {0{,}693}{\lambda }}}$

is a little smaller.

Crookedness

The skewness possesses independently of the parameter always has the value 2. The distribution is a typical representative of a very skewed distribution , for which applies. ${\displaystyle \lambda }$ ${\displaystyle {\tilde {x}}<E(X)}$

Bulge

The curvature always has the value 9 regardless of the parameter . ${\displaystyle \lambda }$

Quantiles

The quantile function of the exponential distribution can be specified and is

${\displaystyle F_{\lambda }^{-1}(p)={\frac {-\ln(1-p)}{\lambda }}}$.

This is the interquartile range . ${\displaystyle {\frac {\ln 3}{\lambda }}\approx {\frac {1{,}10}{\lambda }}}$

Higher moments

The kth moments are

${\displaystyle \operatorname {E} (X^{k})={\frac {k!}{\lambda ^{k}}}}$.

This can be shown, for example, with the k-th derivative of the torque-generating function.

Accumulators

The cumulative generating function is

${\displaystyle g_{X}(t)=\ln \left({\frac {\lambda }{\lambda -t}}\right)}$for . ${\displaystyle t<\lambda }$

This is the kth cumulant ${\displaystyle \kappa _{k}={\frac {(k-1)!}{\lambda ^{k}}}}$

Characteristic function

The characteristic function has the form

${\displaystyle \varphi _{X}(t)={\frac {\lambda }{\lambda -\operatorname {i} t}}}$.

Moment generating function

The moment generating function of the exponential distribution is

${\displaystyle m_{X}(t)={\frac {\lambda }{\lambda -t}}}$for . ${\displaystyle t<\lambda }$

entropy

The entropy of the exponential distribution is

${\displaystyle H(X)=1-\ln(\lambda )}$.

Probability of survival

Since the exponential distribution is also used as a service life distribution and in the technical field as an expression for the reliability of a device, it is possible to use the distribution function to specify related variables such as the survival function and the failure rate . This is how the complement of the distribution function is called the survival function:

${\displaystyle P(X\operatorname {>} x)=1-F(x)=\mathrm {e} ^{-\lambda x}}$

This gives the conditional survival probability related to a point in time ${\displaystyle x_{0}}$

${\displaystyle P(X>x_{0}+x|X>x_{0})={\frac {\mathrm {e} ^{-\lambda (x_{0}+x)}}{\mathrm {e} ^{-\lambda x_{0}}}}=\mathrm {e} ^{-\lambda x}}$

The exponential distribution is a memoryless lifetime distribution, i.e. H. the probability of survival in relation to a certain point in time is independent of the previous age. In contrast to the Weibull distribution , the exponential distribution can only be used for so-called fatigue-free systems

The failure rate results in ${\displaystyle h(x)}$

${\displaystyle h(x)={\frac {f(x)}{1-F(x)}}={\frac {\lambda \mathrm {e} ^{-\lambda x}}{\mathrm {e} ^{-\lambda x}}}=\lambda }$

It is constant in time and space for the exponential distribution and is usually referred to in the literature by the constant λ.

Memory loss

The exponential distribution is memoryless in the following sense : If it is known that an exponentially distributed random variable exceeds the value , then the conditional probability that it exceeds by at least exactly as great as that that an exponentially distributed random variable (with the same parameter ) exceeds the value , formally ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle \lambda }$ ${\displaystyle t}$

${\displaystyle P\left(X\geq x+t\,\mid \,X\geq x\right)=P\left(X\geq t\right)}$.

Memorylessness is even a defining property of the exponential distribution; this is the only possible continuous distribution with this property. This follows directly with the definition of the conditional probability and the resulting functional equation . The discrete counterpart to this is the geometric distribution as the only possible discrete memoryless distribution.

Other properties

Are stochastically independent, so is ${\displaystyle X_{1}\sim \mathrm {Exp} (\lambda _{1}),\,\ldots \,,X_{n}\sim \mathrm {Exp} (\lambda _{n})}$ ${\displaystyle \min(X_{1},\ldots ,X_{n})\sim \operatorname {Exp} (\lambda _{1}+\dotsb +\lambda _{n})}$

If stochastically independent, then there is a linear combination of exponential distributions, if they are all equal, then the sum is Erlang-distributed. ${\displaystyle X_{1}\sim \mathrm {Exp} (\lambda _{1}),\,\ldots \,,X_{n}\sim \mathrm {Exp} (\lambda _{n})}$ ${\displaystyle X_{1}+\ldots +X_{n}}$ ${\displaystyle \lambda _{i}}$ ${\displaystyle \sim \operatorname {Erl} (n,\lambda )}$

Relationship to other distributions

Relationship to constant uniform distribution

If a continuous random variable is uniformly distributed over the interval , then the exponential distribution with the parameter is sufficient . ${\displaystyle X}$ ${\displaystyle [0,1]}$ ${\displaystyle Y=-{\tfrac {1}{\lambda }}\ln(X)}$ ${\displaystyle \lambda }$

Relationship to normal distribution

If the random variables and are standard normal distributed and independent , then is exponentially distributed with parameter . ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X^{2}+Y^{2}}$ ${\displaystyle \lambda ={\tfrac {1}{2}}}$

Relationship to the geometric distribution

In analogy to the discrete geometric distribution , the continuous exponential distribution determines the waiting time until the first occurrence of an event that occurs according to a Poisson process; the geometric distribution can thus be viewed as a discrete equivalent to the exponential distribution.

Relationship to the gamma distribution

• The generalization of the exponential distribution, i.e. H. the waiting time until the occurrence of the -th event of a Poisson process is described by the gamma distribution . The exponential distribution with parameters is therefore identical to the gamma distribution with parameters and . The exponential distribution therefore also has all the properties of the gamma distribution. In particular, the sum of independent, -distributed random variables is gamma or Erlang-distributed with parameters and . ${\displaystyle n}$ ${\displaystyle \lambda }$ ${\displaystyle 1}$ ${\displaystyle \lambda }$ ${\displaystyle n}$ ${\displaystyle \operatorname {Exp} (\lambda )}$ ${\displaystyle n}$ ${\displaystyle \lambda }$

• The convolution of two exponential distributions with the same results in a gamma distribution with , . ${\displaystyle \lambda }$ ${\displaystyle p=2}$ ${\displaystyle b=\lambda }$

Relationship to the gamma-gamma distribution

If the parameter of the exponential distribution is a random variable that is distributed like a gamma distribution, then the resulting random variable is distributed like a gamma-gamma distribution. ${\displaystyle \lambda }$ ${\displaystyle \operatorname {Exp} (\lambda )}$ ${\displaystyle G(a,b)}$ ${\displaystyle G(a,b,1)}$

Relationship to the Pareto distribution

If Pareto is distributed with parameters and , then is exponentially distributed with parameters . ${\displaystyle X}$ ${\displaystyle \operatorname {Par} (\lambda ,1)}$ ${\displaystyle \lambda }$ ${\displaystyle 1}$ ${\displaystyle \log {X}}$ ${\displaystyle \operatorname {Exp} (\lambda )}$ ${\displaystyle \lambda }$

Relationship to the Poisson distribution

The intervals between the occurrence of random events can often be described using the exponential distribution. In particular, it applies that the distance between two successive events of a Poisson process with Rate is exponentially distributed with the parameter . In this case the number of events in an interval of length is Poisson distributed with parameter . ${\displaystyle \lambda }$ ${\displaystyle \lambda }$ ${\displaystyle \Delta w}$ ${\displaystyle \lambda \cdot \Delta w}$

Derivation: Let w be a position or time variable and the small constant occurrence frequency of events in the unit interval of w. Then one finds the probability of the next occurrence of an event in the small interval as the product of the probability of having no event up to w and one in the interval using Poisson's assumptions : ${\displaystyle \lambda }$ ${\displaystyle [w,w+\Delta w]}$ ${\displaystyle [w,w+\Delta w]}$

${\displaystyle P_{1}(w+\Delta w)=\mathrm {e} ^{-\lambda \cdot w}\cdot \lambda \Delta w}$

After division by the probability density, this results in the exponential distribution as the event rate and the mean event distance. ${\displaystyle \Delta w}$ ${\displaystyle f_{\lambda }(w)=\lambda \mathrm {e} ^{-\lambda \cdot w}}$ ${\displaystyle \lambda }$ ${\displaystyle 1/\lambda }$

Relationship to the Erlang distribution

• For a Poisson process, the random number of events up to a defined point in time is determined by means of the Poisson distribution , the random time up to the -th event is Erlang-distributed . In this case , this Erlang distribution changes into an exponential distribution , with which the time to the first random event and the time between two successive events can be determined. ${\displaystyle n}$ ${\displaystyle n=1}$ ${\displaystyle \operatorname {Erl} (\lambda ,1)=\operatorname {Exp} (\lambda )}$

• The sum of independent exponentially distributed random variables has the Erlang distribution -th order . ${\displaystyle n}$ ${\displaystyle \operatorname {Exp} (\lambda )}$ ${\displaystyle n}$ ${\displaystyle \operatorname {Erl} (\lambda ,n)}$

Relationship to the Weibull distribution

• With the Weibull distribution changes into the exponential distribution. In other words, the exponential distribution deals with problems with a constant failure rate . However, if one examines questions with a rising ( ) or falling ( ) failure rate, one moves from the exponential distribution to the Weibull distribution. ${\displaystyle \beta =1}$ ${\displaystyle \lambda }$ ${\displaystyle \lambda >1}$ ${\displaystyle \lambda <1}$
• If is exponentially distributed , then Weibull is distributed. ${\displaystyle X}$ ${\displaystyle X^{\lambda }}$

Relationship to the chi-square distribution

The chi-square distribution changes into the exponential distribution with the parameter . ${\displaystyle n=2}$ ${\displaystyle \lambda ={\tfrac {1}{2}}}$

Relationship to the Rayleigh distribution

If is exponentially distributed with rate , then it is Rayleigh distributed with scale parameter . ${\displaystyle X}$ ${\displaystyle \lambda }$ ${\displaystyle {\sqrt {X}}}$ ${\displaystyle {\frac {1}{\sqrt {2\lambda }}}}$

Relationship to the Laplace distribution

Are two independent random variables, both exponentially distributed with parameters , then both as a Laplacian distributed . ${\displaystyle X_{\lambda },Y_{\lambda }}$ ${\displaystyle \lambda }$ ${\displaystyle X_{\lambda }-Y_{\lambda }}$ ${\displaystyle Y_{\lambda }-X_{\lambda }}$

Relation to the standard Gumbel minimum distribution

The density of the logarithm of a standard exponentially distributed random variable follows a standard Gumbel distribution (minimum) ${\displaystyle X\sim \operatorname {Exp} (\lambda =1)}$

${\displaystyle f(z)=\operatorname {exp} \left(z\right)\operatorname {exp} \left(-\operatorname {exp} \left(z\right)\right)}$ .

Application example

The exponential distribution is a typical lifetime distribution. For example, the service life of electronic components is often distributed approximately exponentially. In this context, the lack of memory plays an important role: the probability that a component that is x days old will last at least t days is therefore just as great as that a new component will last t days at all. The constant failure rate is characteristic of the exponential distribution . ${\displaystyle \lambda }$

This is only approximately correct for incandescent lamps, for example, since they are only heavily used when they are switched on. Exponential distribution must not be applied to living beings either, otherwise the probability that an eighty-year-old will live another fifty years, for example, would be just as high as that of a newborn child reaching the age of fifty.

Example: Radio alarm clocks are produced in an electronics company. As part of quality assurance, the functional duration of the alarm clock is examined on the basis of complaints. It turns out that an average of 5 ‰ of the alarm clocks fail every day regardless of their age.

The random variable “duration of the functionality of a radio alarm clock in days” is exponentially distributed with the failure rate . Accordingly, the average time it takes for an alarm clock to fail is days. ${\displaystyle X=}$ ${\displaystyle \lambda =0{,}005}$ ${\displaystyle 1/\lambda =200}$

The probability that an alarm clock will last for a maximum of 20 days is

${\displaystyle 1-\mathrm {e} ^{-0{,}005\cdot 20}=0{,}0952}$

d. H. after 20 days, an average of about 10% of the alarm clocks have failed.

Accordingly, the proportion of alarm clocks that last for at least 180 days is

${\displaystyle 1-\left(1-\mathrm {e} ^{-0{,}005\cdot 180}\right)=1-0{,}5934=0{,}4066}$

so on average about 40% of the alarm clocks last longer than 180 days.

Although more devices fail at the beginning with an exponentially distributed lifetime distribution, the failure rate is constant: in relative terms, the same number of devices fail in each time interval. This fact must not be confused with the early failures of the bathtub curve . Here the failure rate is higher at the beginning and not constant over the service life. A different lifetime distribution ( Weibull distribution ) is necessary to describe the bathtub curve . ${\displaystyle \lambda }$

Random numbers

The inversion method can be used to generate exponentially distributed random numbers .

The inverse of the distribution function to be formed according to the simulation lemma reads here . A sequence of exponentially distributed random numbers can therefore be calculated for a sequence of standard random numbers . Instead, it is easier to calculate. ${\displaystyle F(x)=1-\mathrm {e} ^{-\lambda x}}$ ${\displaystyle F^{-1}(y)=-{\tfrac {1}{\lambda }}\ln(1-y)}$ ${\displaystyle u_{i}}$ ${\displaystyle x_{i}:=-{\tfrac {1}{\lambda }}\ln(1-u_{i})}$ ${\displaystyle x_{i}:=-{\tfrac {1}{\lambda }}\ln(u_{i})}$

See also

• Mortality (transition from the exponential distribution to the Weibull distribution)
• List of univariate probability distributions

Web links

• University of Konstanz - Interactive animation
• www.exponentialgabe.de - Explanation, tasks, illustration