Mean time between failures

Mean Time Between Failures ( MTBF for short ) is the English term for the mean operating time between failures for repairable units. "Operating time" means the operating time between two successive failures of a repairable unit.

The definition according to IEC 60050 (191) is: The expected value of the operating time between two successive failures.

For units not be repaired (can), the expected value (mean) is the distribution of lives the average life MTTF ( English mean time to failure ). Colloquially, the terms are often used synonymously (in this case the backronym "mean time before failure" has become established).

illustration

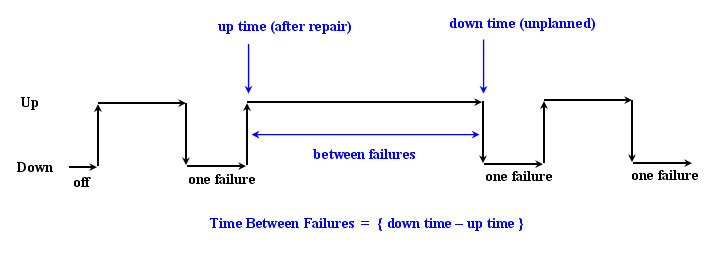
MTBF is a measure of the reliability of units ( assemblies , devices or systems ) that are repaired ( up ) after a failure ( down ) . This behavior can be illustrated using the following graphic:

The operation of the unit lies between the event of commissioning ( up-time ) and the event of failure ( down-time ). Formally, the MTBF can be expressed over a long period of time, in which many failures and startups are to be expected, as:

${\displaystyle {\text{MTBF}}={\frac {\Sigma {({\text{start of downtime}}-{\text{start of uptime}})}}{\text{number of failures}}}.}$

The value n indicates the number of failures over the long period under consideration, up-time is the duration of the entire period and down-time is the sum of the failure times.

The higher the MTBF value, the more reliable the device is. A device with an MTBF of 100 hours will on average fail more often than a similar device with an MTBF of 1000 hours. The mathematical probability that a device will achieve this MTBF time without failure when used within its regular service life and operating conditions is 37%.

If MTBF information is provided, the environmental and function-related stresses, the failure criteria and the period of validity should also be specified (e.g. ambient temperature, number of start / stop cycles per day, compliance with maintenance regulations, etc.). Under unfavorable operating conditions, significantly lower MTBF values ​​(higher failure rates) than expected can occur. On the other hand, derating (and the lower failure rate resulting from this oversizing) can increase the MTBF.

The MTBF must be differentiated from the useful life of a device: The useful life indicates the length of time a device was designed for during development. She is u. a. determined by the dimensioning of wear parts.

Calculation bases

In both the mathematical determination and the application of MTBF values ​​for reliability prognosis, it is fundamentally assumed that the units under consideration ( assemblies , devices or systems ) are used during their service life and under specified operating conditions. It is therefore assumed that the unit under consideration is operated in the middle area of ​​the "bathtub curve" , ie with a constant failure rate . This period, known as the exponential distribution , rules out premature and attrition failures.

MTBF is calculated from the reliability function R ( t ). If the probability density for a failure at time t , then the following generally applies: ${\displaystyle f(t)}$

${\displaystyle \mathrm {MTBF} =\int _{0}^{\infty }R(t)\,dt=\int _{0}^{\infty }tf(t)\,dt}$

For the above The case of a unit operating during a period of constant failure rate applies . Thus, the MTBF of a unit results from the reciprocal of the constant failure rate λ of this unit: ${\displaystyle f(t)=\lambda e^{-\lambda t}}$

${\displaystyle \mathrm {MTBF} ={\frac {1}{\lambda }}.}$

This relationship between failure distance and failure rate of a unit allows a simple determination or conversion in the above. Period of service life.

If the MTBF of a unit is known, a probable statement of survival up to a certain point in time can be given. For example, the failure probability of a component or device up to the MTBF is 63.2% (exactly 1-1 / e) . Thus, after reaching the time corresponding to MTBF, only about 37% of the units present at the start of the test are still functional and about 2/3 of the units have failed. These statements assume that the unit under consideration is operated in the middle area of ​​the "bathtub curve" , ie with a constant failure rate , so that there are no systematic failures. They also refute the often made assumption that MTBF has an average service life (50% failures).

Applications

The MTBF value can be used as a measure of the reliability of components and devices or to compare different devices or designs. However, this value can only be understood to a limited extent as the “mean service life” in the sense of an average value.

Estimated values ​​for the MTBF can be determined through service life tests - in some cases also with increased stresses - in which the device z. B. radiation , moisture, vibrations, heat and the like is exposed, such. B. a Highly Accelerated Life Test . The MTBF is the reciprocal of the failure rate of the assembly / unit determined in this way. These tests are not standardized , which is why all specified MTBF values ​​are only comparable within the product series of one manufacturer.

The MTBF can be used to estimate failures in time intervals. For example, MTBF values ​​of 1,200,000 hours (WD RE3 500G) are common for hard drives, which corresponds to 137 years. This number can be used to calculate the probability that a failure will occur during the service life (often 5 years for hard drives). It amounts to approximately:

${\displaystyle {\begin{aligned}p(T)&=1-e^{-{\frac {T}{\mathrm {MTBF} }}}\\p(5a)&=1-e^{-{\frac {5a}{137a}}}=3{,}6\,\%\end{aligned}}}$

With this application for reliability prognosis, knowing the MTTF values ​​can be used to estimate whether set reliability goals can be achieved. This requires precise knowledge of the structure of the device and the failure rates of the components used (failure rates are often given in FIT (1 FIT = 10 ⁻⁹  h ⁻¹ ), failure in time ). The MTBF is the reciprocal of the calculated failure rate of the assembly / unit, which in turn results from the sum of the component failure rates weighted depending on the stress.

When calculating the MTBF from FIT, it must be taken into account that FIT is usually specified without the unit “failures per 10 ⁹ hours”. If, for example, the MTBF of a repairable device is determined by a component for which FIT is known, then the following conversion formula results for the expected mean time that will elapse between the replacement of this component by a new component:

${\displaystyle \mathrm {MTBF} ={\frac {10^{9}\,{\text{Stunden}}}{\mathrm {FIT} }}={\frac {114000\,{\text{Jahre}}}{\mathrm {FIT} }}}$

Example: For a FIT of 1140 this results in MTBF = 100 years.

The MTBF is also used for the calculation of the "stationary" Availability (engl. Availability ) are used. The availability indicates the probability that a system will offer the specified service when requested:

${\displaystyle A={\frac {\mathrm {MTBF} }{\mathrm {MTBF} +\mathrm {MTTR} }}}$

From a business point of view, the MTBF is used as a key figure for measuring performance ( Key Performance Indicator , KPI ).

MTBF of composite systems

The overall availability of a system can be calculated from the availability or the MTBF of subsystems. A system can be composed in series of two subsystems a and b, i.e. H. both subsystems must be available for the overall system to function. The following then applies to the availability of the overall system

${\displaystyle A_{\text{seriell}}=A_{a}\cdot A_{b}}$

If one assumes the same mean recovery time MTTR for the partial and overall systems, one obtains for the series connection:

${\displaystyle \mathrm {MTBF} _{\text{seriell}}={\frac {1}{{\frac {1}{\mathrm {MTBF} _{a}}}+{\frac {1}{\mathrm {MTBF} _{b}}}+{\frac {\mathrm {MTTR} }{\mathrm {MTBF} _{a}\cdot \mathrm {MTBF} _{b}}}}}}$

If a system is built up in parallel from two functionally identical redundant subsystems a and b, then only one of the subsystems needs to be available for the overall system to work. The following applies to the availability of the overall system

${\displaystyle A_{\text{parallel}}=1-(1-A_{a})\cdot (1-A_{b})}$

If one again assumes the same mean recovery time MTTR for the partial and overall system, one obtains for the parallel connection:

${\displaystyle \mathrm {MTBF} _{\text{parallel}}={\frac {\mathrm {MTBF} _{a}\cdot \mathrm {MTBF} _{b}}{\mathrm {MTTR} }}+\mathrm {MTBF} _{a}+\mathrm {MTBF} _{b}}$

In all cases it is assumed that the repair of the subsystems will start immediately after the failure, especially if the overall system is still functioning due to a redundant design. More complex systems can be put together from parallel and series connections and calculated accordingly.

Similar terms

• Mean Distance Between Failure (MDBF)
• Mean Time Between Maintenance (MTBM)
• Mean Time Between Unscheduled Removal (MTBUR)
• Mean Time To Failure (MTTF)
• Mean Time To Recover (MTTR)
• Mean Time Between Overhaul (MTBO)
• Mean Cycles Between Failure (MCBF)
• Mean Time Between Critical Failure (MTBCF)

Norms

There are standards for the calculation, for example

• DIN EN / IEC61709
• SN 29500 from Siemens AG (is continuously updated, in addition to electronic components, more and more electromechanical components such as relays , contactors , circuit breakers , overload relays , time relays , etc. Command and signaling devices, pushbuttons , indicator lights , position switches are in progress)
• SR-332 from Telcordia Technologies
• U.S. Military MIL-HDBK-217 (no longer maintained)

Individual evidence

1. ↑ ^{a b c d} J. Lienig, H. Brümmer: Reliability of electronic devices . In:  Electronic device technology . Springer Vieweg, 2014, ISBN 978-3-642-40961-5 , pp. 55-58.
2. ↑ Alessandro Birolini: Appendix A1 - Definitions . In: Ders .: Reliability of devices and systems . 4th edition Springer Verlag, Berlin 1997, ISBN 3-540-60997-0 .

literature

• Patrick Gehlen: Functional safety of machines and systems. Implementation of the European Machinery Directive in practice . 1st edition. Publicis Corporate Publishing, 2010, ISBN 978-3-89578-281-7 .
• Alessandro Birolini: Reliability of devices and systems . 1st edition. Springer, 1997, ISBN 3-540-60997-0 .
• Alessandro Birolini: Reliability Engineering: Theory and Practice . 7th edition. Springer, 2013, ISBN 978-3-642-39534-5 .
• Jens Lienig, Hans Brümmer: Electronic device technology . 1st edition. Springer, 2014, ISBN 978-3-642-40961-5 .

Web links

• More detailed explanation of the MTBF (English, pcguide.com)
• another explanation about MTBF (English, storagereview.com)
• Elaboration of MTBF using the example of hard disks (English)
• "MTBF" & "MTTR" briefly explained , edinn
• Briefly explained: hard disk lifespan , iX
• BQR Care MTBF Commercial MTBF software